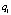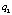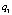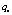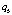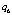Scientific journal

International Journal of Experimental Education

ISSN 2618–7159

ИФ РИНЦ = 0,425

В настоящее время квадрокоптеры используются достаточно широко и разнообразно, но это использование ограничено, в основном, режимами «ручного» дистанционного управления с пульта оператора. Актуальной является задача разработки системы управления, позволяющая осуществлять автономный полёт квадрокоптера по заданному маршруту.

Разные методы контроля были изучены для управления угловым положением и траекторным движением квадрокоптера. Способ управления наиболее часто используемых является PID, LQR, скользящий режим. LQR является способ управления классическая линейная, но не подходит для систем с сильной нелинейностью и сцепные характеристики[1]. Таким образом, эти контроллеры работают только лучше, когда квадрокоптер в зависший состояние. Скользящий режим является еще одним мощным средством управления [2], который является простым и надежным. Но, скольжения режим управления требует постоянного логику переключения, что приводит к болтовня явления. Метод бэкстеппинг на основе функций Ляпунова также используется для контроля quadrotor [3]. Гибридный контроллер на основе бэкстеппинг и нечеткой адаптивной PID была предпринята в ссылки[4]. Метод выбирает регулятор ПИД или бэкстеппинг, в соответствии с условиями полета квадрокоптера. А контроллер управления отслеживанием траектории для квадрокоптера на основе регулятора PD и бэкстеппинг с фильтором был предложен в качестве ссылки [5]. Нелинейный контроллер на основе нейронной сети и вывода обратной связи был изучен в ссылке [6, 7]. Онлайн предотвращения столкновений алгоритм планирования траектории на основе Пифагора годографа (PH) кривая и бэкстеппинг был представлен в ссылки[8]. В работе [9] адаптивной контроллер позиции отслеживания управления предлагается для вертикального взлета и посадки для набора ограниченных внешних возмущений.

В этой статье предлагается алгоритм управления угловым положением, траекторным движением квадрокоптера на основе многорежимного контроллера, составляющий наборов ПИД-регуляторов и бэкстеппинг-регуляторов. Алгоритм автоматическо выбирает подходящий набор регулятора в соответствии с условиями полёта (высота, угловое положение, ветровые воздействия, режимы взлёта-посадки, расстояние до заданной траектории).

Математическая модель квадрокоптера

При моделировании полёта квадрокоптера, дальность и продолжительность которого весьма ограничены, можно пренебречь движением Земли, т.е. считать земные системы координат инерциальными. На начальных этапах разработки можно также считать ненесущую часть аппарата твёрдым телом, а ветер учитывать только как внешнее возмущение.

Сила тяги в связанной системе координат и нормальной земной системе координат:

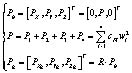(1)

где P – суммарная тяга; 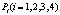 – сила тяги i-го винта; 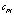– коэффициент силы тяги; R – матрица перехода; 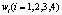– скорость вращения i-го винта.

Сила сопротивления воздуха и сила тяжести:

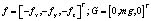(2)

где m – масса квадрокоптера; g – ускорение силы тяжести.

Уравнения динамики движения центра масс в нормальной земной системы координат:

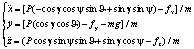(3)

где 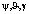– углы рыскания, тангажа, крена.

С учетом симметрии аппарата и считая, что центр масс расположен в начале координат связанной системы, уравнения динамики углового движения в связанной системе координат можно записать в виде

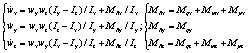(4)

где 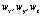 – проекции вектора угловой скорости аппарата на связанную систему координат; 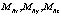– проекции результирующего момента;  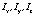– осевые моменты инерции аппарата; 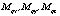– моменты, создаваемые винтам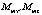и, и 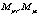 – гироскопические моменты двигателей и винтов. Если пренебречь инерционностью винтов при изменении угловых скоростей их вращения, то указанные моменты можно выразить следующим образом:

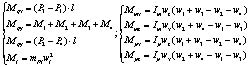(5)

где l – расстояние от центра масс до оси винта, 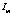и 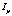– моменты инерции ротора и винта; 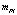– коэффициент момента.

Изменения углов Эйлера определяются через проекции угловой скорости кинематическими уравнениями Эйлера:

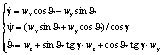(6)

Многорежимный контроллер

Задачу траекторного управления полётом квадрокоптера можно рассмотреть как последовательность задач перелёта в очередную заданную точку маршрута или движения по заданным участкам типовых траекторий. В этом случае система автоматического управления может быть построена как система с обратной связью, осуществляющая отслеживание заданного маршрута. При этом можно выделить канал управления высотой и канал управления движением в горизонтальной плоскости. Стабилизация и управление в вертикальном направлении обеспечивается изменением суммарной величины тяги. Горизонтальное перемещение аппарата происходит под действием горизонтальной проекции суммарного вектора тяги, отклонённого от вертикали. В рассматриваемом варианте отклонение вектора тяги происходит за счёт изменения углов тангажа и крена при фиксированном положении угла рыскания. Изменение углового положения достигается путем дифференцированного управления скоростями вращения винтов, дающего соответствующие различия их сил тяги и моментов. Подсистему, обеспечивающую необходимые значения угловых параметров и высоты за счёт изменения тяги винтов, можно назвать системой ориентации и стабилизации, а подсистему, осуществляющую отслеживание заданных траекторий – системой траекторного управления.

Структура системы управления показана на рис. 1, где цифрами обозначены: 1 – заданная траектория; 2 – корректирующие устройства (КУ) подсистемы траекторного управления и переключатель устройств; 3 – преобразователь координат; 4 – регуляторы подсистемы ориентации и стабилизации переключатель регуляторов; 5 – распределитель сигналов; 6 – ограничитель напряжения; 7 – модель винтомоторной группы; 8 – модель квадрокоптера; 9 – преобразователь режимов полета; 10 – ограничитель скорость посадки.

Алгоритмы работы подсистем стабилизации и траекторного управления предлагается рассчитывать одним из известных методов, причём предпочтительнее выбирать те, которые при сравнимом качестве являются наиболее простыми. Поэтому для каждой из подсистем произведен расчёт корректирующих устройств в виде ПИД-регуляторов и методом, известным в литературе под названием «бэкстеппинг» (англ. backstepping) , после чего путём сравнения результатов выбран наиболее подходящий регулятор для каждой из подсистем.

Чтобы избежать повторов в изложении, расчёт регуляторов для каждой из подсистем показан на примере одного из методов: «бэкстеппинг» – для алгоритма стабилизации углового положения; ПИД-регуляторы – для алгоритма отслеживания траекторий.

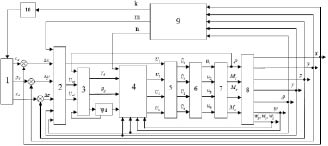
Рис. 1. Схема системы управления квадрокоптера

Преобразователи режимов полета

Известно, что чем меньше угол тангажа и крена, тем устойчиво летает квадрокоптер. В реальном случае, существуют влияния эффекта земли и ветра. Эти факторы могут привести к потере устойчивости полета квадрокоптера и отклонениему от заданной траектории, даже столкновениему. Алгоритм многорежимного управления, реализуемый на микроконтроллере, содержит набор ПИД-регуляторов и бэкстеппинг-регуляторов может эффективно решить эти проблемы. Контроллер выбирает подходящий набор регулятора с разных коэффицентов, в соответстии с состояниями полета квадрокоптера. Выбираем угол тангажа, угол крена, высота полета, и расстояние между квадрокоптером и заданной траектории для входа переключателя многорежимного контроллера. Если квадрокоптер в режиме взлета или посадки, то есть высота полета меньше определенного порога: 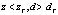или 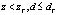(d – горизонтальное расстояние от целевой точки; 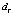– порог посадки), эффект земли очевидный, необходимо выбираем регулятор с меньше перерегулированием для избегания столкновения с землей и уменьшения дрожания квадрокоптера. Если квадрокоптер летает в среде с меньшее слабом ветром или слабом ветром, то есть угла тангажа и крена меньше порога угла устойчивост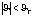и: и 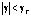необходимо выбираем регулятор с гладкой кривой для повышения устойчивости полета квадрокоптера. Если квадрокоптер летает в среде с умереном ветром или расстояние между квадрокоптером и заданной траектории больше порога сближения, то есть угла тангажа, крена больше порога угла устойчивост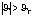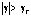и: , или 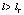необходимо выбираем регулятор с коротком времени регулирования для повышения скорости корректирования своеотношения полета квадрокоптера. Если квадрокоптер летает в среде с скверной погодой или появляется отказ оборудования в процессе выполнения задачи полета, то есть угла тангажа или крена больше порога угла бесопасност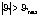и: или 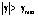, то необходимо прервать задачу и возвращается к базе.

Множество режимов полета:

,

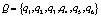где 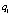– взлет; 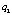– посадка; 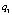– полета в среде с меньшее слабом ветром или слабом ветром со скоростью меньше 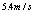; 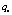– полетав среде с умерном ветром со скоростью меньше 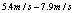; 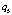– режим быстрой регулировки отклонения;  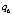– режим защита .

Множество дискретных событий:

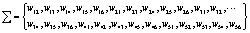
где 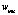– дискретное событие переключения из режима m в режим n.

Схема перехода режимов показана на рис. 2.

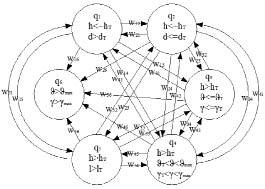
Рис. 2. Диаграмма преобразования режима

Алгоритмы стабилизации углового положения

Входами подсистемы ориентации и стабилизации углового положения являются задаваемые подсистемой траекторного управления сигналы 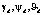, а выходами – параметры углового движения объекта. Управляющий алгоритм этой подсистемы должен формировать управляющие сигналы U2, U3, U4, обеспечивающие создание необходимых моментов MRx, MRy, MRz, при условии, что суммарная тяга винтов будет соответствовать необходимой для вертикального движения. Если пренебречь динамикой и ограничениями двигателей, гироскопическими моментами и аэродинамическими моментами ненесущей части аппарата, то сигналы U2, U3, U4  должны быть с точностью до коэффициента равными моментам MRx, MRy, MRz. Поэтому моделью объекта для алгоритма стабилизации являются уравнения (5) при MRx = U2, MRy = U3, MRz = U4.

Суть метода «бэкстеппинг» состоит в представлении сложной системы в виде цепочки вложенных подсистем, для каждой из которых формируются вспомогательные управляющие сигналы и составляются зависящие от этих сигналов функции Ляпунова. Выполнение критериев устойчивости по Ляпунову при последовательном выборе этих сигналов для каждой подсистемы обеспечивает устойчивость системы в целом. Процедура имеет характер пошагового обхода интеграторов обратными связями, откуда – название «integrator backstepping», или кратко – бэкстеппинг (англ. backstepping). В определённых частных случаях процедура становится регулярной и достаточно простой. Для углового движения летательного аппарата такой случай возможен при малых углах тангажа и крена, когда производные углов 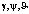можно считать равными соответствующим угловым скоростям. Тогда уравнения углового движения (5) можно приближённо представить в виде трёх подсистем

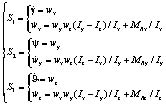(7)

Следуя приведённому в алгоритму, введём для подсистемы S1 вспомогательный управляющий сигнал 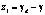и соответствующую функцию Ляпунова 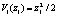, производная которой 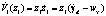. Второй вспомогательный управляющий сигнал сформируем в виде 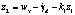с соответствующей функцией Ляпунова 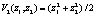, производная которой 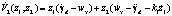. Принимая для системы стабилизации 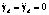, получаем

.

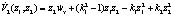Чтобы подсистема была устойчива, то есть, чтобы 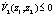, причём 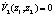только когда 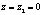, примем

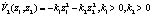. (8)

Тогда управляющий сигнал будет иметь вид:

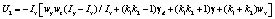. (9)

Функция Ляпунова

,

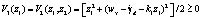а её производная 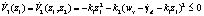, то есть замкнутая подсистема – устойчива.

Аналогичным образом можно получить другие управляющие сигналы:

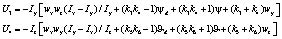(10)

Алгоритмы траекторного управления

Проекции горизонтальной силы без учёта сопротивления ненесущей части аппарата согласно уравнениям динамики имеют вид:

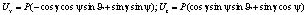, (11)

откуда можно определить углы крена и тангажа, при которых создаются требуемые воздействия при известной суммарной тяге P:

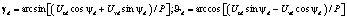. (12)

Необходимо обратить внимание, что такой подход к траекторному управлению предъявляет очень высокие требования к быстродействию и точности подсистемы ориентации и стабилизации, что вызывает необходимость в более глубоком исследовании, выходящем за рамки настоящей статьи. Здесь будем считать результат удовлетворительным, если он подтверждается моделированием.

Управляющие воздействия Uxd и Uzd, а также Uyd = U1 для канала управления высотой, можно получить, рассматривая подсистему траекторного управления как систему регулирования, отслеживающую требуемые координаты центра масс, в частности – как выходные сигналы ПИД-регулятора по отклонениям координат центра масс от требуемых:

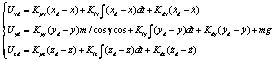(13)

Результаты моделирования

Работоспособность алгоритма проверялась моделированием реакций на ступенчатые воздействия и полёта по заданным траекториям. Схема моделирования в среде Matlab Simulink показана на рис. 3.

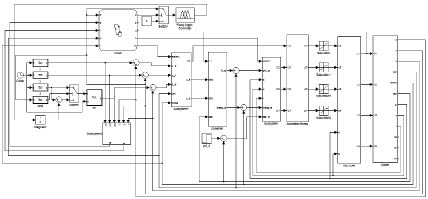
Рис. 3. Схема моделирования системы управления

На рис. 4 показывается реакции на ступенчатое воздействие трех видов регуляторов (здесь только рассмотрим каналы x и 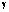): ПИД1 и БЭК1 – прочные ПИД и бэкстеппинг регуляторы; ПИД2 и БЭК2 – ПИД и бэкстеппинг регуляторы с гладкой кривой и меньше перерегулированием; ПИД3 и БЭК3 – ПИД и бэкстеппинг регуляторы с коротком время реакции.

В таблице показаны соответствия режимов полета квадрокоптера и выборов регуляторов.

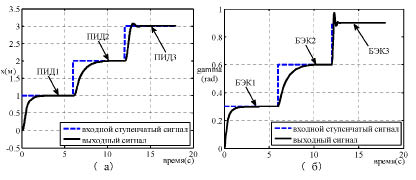
Рис. 4. Реакции на ступенчатое воздействие: а – пид-регулятор; б – бэкстеппинг-регулятор

Соответствия режимов полета и регуляторов

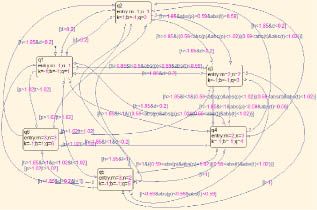
Рис. 5. Преобразование режимов полета

Рис. 5. показывает преобразование режимов полета квадрокоптера и условия преобразований в модули состояние потока (stateflow) Matlab.

На рис. 6 показаны результаты моделирования при отслеживании траектории состоящей из участков: AB – взлет; BC – равномерное прямолинейное движение; CD – равномерное ускоренное прямолинейное движение; DE – равномерное движение вокруг точки (5,10,15) по горизонтальному кругу радиусом 5 м; EF – равномерное прямолинейное движение; FG – равномерное движение вокруг точки (-5,10,10) по горизонтальному кругу радиусом 10 м.; GH – посадка. Результаты в целом удовлетворительны, хотя видны возможности улучшения: устранение перерегулирования по высоте и ускорение процессов.

На рис. 7 показаны сравнения изменений угловых положений (γ,ϑ) многорежимного контроллера и стандартного контроллера, созданного из прочных регуляторов. В соответствии с результатами квадрокоптер летит более устойчиво под управлением многорежимного контроллера.

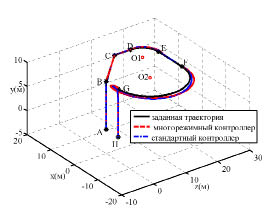
Рис. 6. Отслеживание траектории

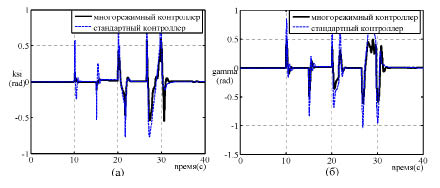
Рис. 7. Изменения углового положения: а – ϑ; б – γ

Выводы

Разработана математическая модель квадрокоптера как объекта управления. Представлена разработка алгоритма управления, который позволяет стабилизировать высоту, угловое положение и координаты полета квадрокоптера и отслеживать заданную траекторию. Разработка многорежимного контроллера, позволяющего работать квадрокоптер в разных режимов. Результаты моделирования показывают работоспособность алгоритма и возможность его реализации.