Реконструция окружающей среды является важной разработкой при решении задачи обхода препятствий, планирования маршрута и навигации и т.д. для роботов, как наземных, так и воздушных. Облачно-точечная карта имеет простую структуру, хотя в ней тольно содержаются информации о координаты угловых точек, но уже достотчно для выражения окружающей среды. В настоящее время роботы получают информацию об окружающей среде с помощью GPS, лазерного радара, компьютерного зрения и других датчиков. Учёные Surmann, Nuchter и их коллеги воспроизвели окружающую среду, используя трёхмерный лазерный радар [1], однако лазерный радар имеет высокую стоимость и большие габариты, поэтому он трудно применим для роботов в процессе решения задачи в режиме реального времени. Компьютерное зрение имеет преимущества – невысокая стоимость, высокая точность и малая зависимость от окружающей среды [2 – 4]. В последние годы компьютерное зрение широко используется для решения задачи навигация и получения информации об окружающей среде.
В данной статьей предлагается метод реконструкции облачно-точечной карды окружающей средой в режиме реального времени на основе монокулярного компьютерного зрения. Метод состоит из этапов: обнаружение угловых точек на изображениях из двух соседних кадрах по алгоритму SUSAN; поиск соответствующих угловых точек по алгоритмам NCC и RANSAC; расчёт фундаментальной и существенной матрицы, матрицы вращения и перемещения камеры, и координаты угловых точек изображений в неподвижной системе координат.
Детектор угловых точек
В настоящее время существуют много алгоритмов обнаружения угловых точек, например алгоритм Harris, алгоритм FAST, алгоритм FASTER, алгоритм Shi-Tomas, алгоритм Moravec, алгоритм SUSAN и другие [5]. При сравнении результатов моделирования, в данной работе выбраем алгоритм SUSAN, предложеный Смитом и Бреди (Smith и Brady, 1997) [6], который является более быстрым и устойчивым в случае аффинных преобразований, размытия и неравномерной яркости фона изображений.
В данной статье выбираем фотографии цветов в качестве объекта эксперимента, его пиксельный размер 377×300, показана на рис. 1.
Результаты моделирования детекта угловых точек с помощью популярных существующих детекторов, показаны в табл. 1.
Рис. 1. Изображение для моделирования
Таблица 1
Сравнение результатов моделирования
|
Детектор |
Количество углых точек |
Время вычисления(с) |
|
SUSAN |
76 |
0.119656 |
|
SHI-TOMAS |
83 |
0.226599 |
|
FAST |
81 |
0.419949 |
|
MORAVEC |
79 |
0.428520 |
|
HARRIS |
72 |
0.620711 |
Грубое соответствие угловых точек
Считаем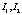 
– яркости первого и второго изображения; 
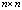(n – нечетное число) – пиксельный размер окна соответствия; 
, 
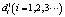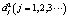и 
, 
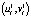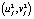– угловые точки и их пиксельные координаты первого и второго изображения. Используем функцию нормированной взаимной корреляции NCC(Normalized cross correlation)[7] для описания корреляции между угловыми точками двух изображений. Эту функцию можно записать в следующим образом:
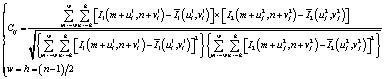(1)
С учётом интервал между соседних кардах очень короткий, в целях повышения правильности и скорости соответствия угловых точек, в этой статье сделаны следующие улучшения для алгоритма NCC. На рис. 2 показана схема соответствия угловых точек.
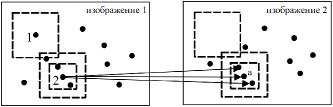
Рис. 2. Схема соответствия характерных точек
1) На первом изображении выбираем окно поиска, имеющое пиксельный размер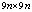 
, вокруг первой угловой точкой. Если в соответствующем окне поиска на втором изображении нет угловых точек (например точка 1 на рис. 2), то перемещаемся окно поиска к следующей угловой точке; если в соответствующем окне поиска есть угловые точки(например точка 2 на рис. 2), то сократить пиксельный размер окна поиска до 
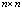и выбираем точку с самой большой корреляции(например точка 2 и точка а на рис. 2) в качестве соответствующей угловой точкой. На конеце получаем множество пар соответствующих угловых точек A.
2) Повторим выше операцию для второго изображения и получаем множество B.
3) Окончательное множество пар угловых точек C является пересечением множеств A и B, т.е. C (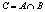
).
Работоспособность улучшенного алгоритма проверялась сравнением результатов поиска сооветствия угловых точек двух изображений соседних кадрах. Результаты показаны в табл. 2.
Таблица 2
Результаты улучшения алгоритма грубого согласования
|
NCC |
Изображения |
Время вычисления |
Количество пар |
|
традиционный |
|
0.207047 |
47 |
|
улучшенный |
|
0.065391 |
53 |
Сравнение результатов показывает, что время вычисления значительно сокращается и количество пар соответствия угловых точек не уменьшается.
Точное согласование
После грубого соответствия ещё есть возможность существования неправильных пар соответственных угловых точек в матрице С. Поэтому необходимо разработка точного соответствия с помощью алгоритма RANSAC [7]. В алгоритме RANSAC реализована самая общая схема устойчивой оценки с помощью выбора случайных подмножеств данных. Схема алгоритм RANSAC записана на рис. 3.
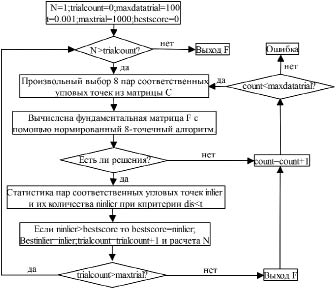
Рис. 3. Схема алгоритм RANSAC для точного соответствия угловых точек
На рисунке inlier – хорошие точки, удовлетворяющие модели; outlier –ложные точки; N – количество набора, определяется следующим уравнением:
;
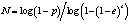e – вероятность выбора без инлаера из общего числа точек; p – вероятность того, что алгоритм RANSAC на некоторой итерации; s=8; trialcount – количество итераций алгорима; maxdatatrial – максимальное количество итераций попытока точки inlier; t – порог расстояние, используемое для определения точки inlier; maxtrial – максимальное количество итераций; bestscore – количество точки inlier предыдущого итерации.
Для повышения устойчивости алгоритма соответствия, сделаны следующие улучшения:
а) Разработка нормализации координаты угловых, так что все точки находится в окружности вокруг центра масса изображения с радиусом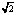 
.
Матрица преобразования:
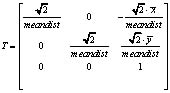(2)
где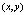 
– координат угловых точек; 
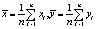– средние координаты угловых точек; n – количество угловых точек;
.
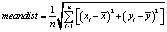б) Использовано расстояние Sampson в качестве критерии определения точек inlier, которое можно записать в следующем образом:
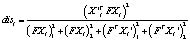(3)
где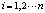 
, 
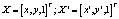– нормализованных соответствующих угловых точек первого и второго изображения; 
(
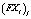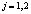) – j-го элемента матрицы 
.
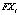Реконструкция окружающей среды
Для получения координаты угловых точек сначало необходимо калибровка внутренней параметров самеры. Использование Камеры Калибровка Набор инструментов для Matlab, написанный Калифорнии политехнического университета доктора Bouquet[8], мы можем получить внутренния параметры камеры :
Фокусное расстояние: fc = [1015.78212 1012.65800] ± ± [7.15609 7.22421 ]
Центральная точка: cc = [320.03704 240.40334] ± ± [ 3.41690 4.77241]
Искажение: kc = [ 0.09333 -0.05262 -0.01156 -0.00424 0.00000 ] ±[ 0.02113 0.11162 0.00246 0.00249 0.00000 ]
Матрица искажения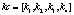 
, где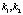 
– параметры радиальных искажениях, 
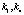– параметры касательных искажениях.
По результату эксперимента калибровки получаем матрицу внутреней параметров камеры:
(4)
Существенная матрица можно записать в следующем образом: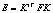 
.
В данной статье мы пользуем монокулярное компьютерное зрение, поэтому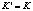 
.
По статьей [9] узнаем, что матрицы вращения и перемещения камеры могут быть получины из уравнений:
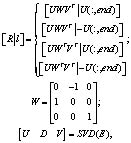(5)
где R– матрица вращения; l – матрица перемещения изображений;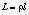 
– матрица перемещениякамеры; 
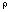– коэффициент пропорции.
Выше уравнения имеют 4 решения, из которых необходимо выбрано единственное правильное решение при критерии: все угловых точки должны находиться перед камерами, т.е., проекция координаты угловых точек на оси z должно быть больше нуля).
Формула проекции матрицы можно записать следующем образом:
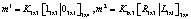(6)
Преобразование координат угловых точек:
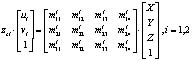,(7)
где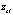 
– проекция координат угловых точек на оси z камерной системы координаты; 
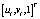– однородные пикмельные координат угловых точек; 
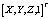– однородные координаты угловых точек в неподвижной системе координат.
Четыре линейных уравнений может быть получена:
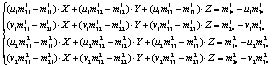(8)
Они переопределённые уравнения, но метод наименьших квадратов может быть использован для решения уравнений. Таким образом, трехмерные координаты угловых точек (X, Y, Z) могут быть получены.
Результаты эксперимента
Чтобы проверить правильность алгоритма реконструкции трехмерной координаты, эксперимент был в помещении. Предмет этого эксперимента был коридор (рис. 4).
а
б
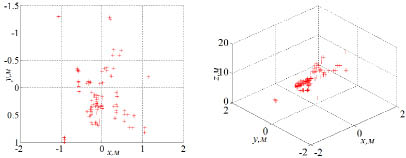
Рис. 4. Реконструкция координаты угловых точек: а – детект и соответствие угловых точек; б – двухмерные и трехмерные координаты угловых точек
На рис. 4, по сравнениему положения характерных точек на изображения и их двухмерных и трехмерных координат, узнаем что координаты характерных точек приблизительно отражают их положения в неподвижной системе координат, то можно доказать правильность метода. Время реакции равно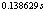 
, что доказывает быстродействие метода.
Выводы
В данной работе предлагается метод реконструкции облачно-точечной карды окружающей средой в режиме реального времени на основе монокулярного компьютерного зрения. По сравнениему результатов моделирования детекта угловых точек выбираем детектор SUSAN, имеющий быстрее скорость вычисления и высше устойчивость. Разработка улучшения грубого и точного алгоритма соответствия, позволяющая повышить скорость вычисления. Результаты эксперимента доказывают правильность и в режиме реального времени предложенного метода.