В представленной работе описывается процесс джинирования, где происходит механическое отделение волокна от семян при помощи зубьев пил. Данный процесс описывается в зоне взаимодействия пил с сырцовым валиком и колосниками в рабочей камере.
В процессе джинирования происходит механическое отделение волокна от семян при помощи зубьев пил, которое происходит в зоне их взаимодействия с сырцовым валиком и колосниками в рабочей камере. Механизм съема волокна с поверхности сырцового валика достаточно сложный и в настоящее время мало изученный [1-2]. В работе [2] определена величина силы трения между волокнами и зубьями пил, установлено, что эта сила переменная вдоль дуги взаимодействия и играет существенную роль в динамике отделения волокна от семян. В этой работе не анализировали закон распределения контактной силы взаимодействия сырцового валика с зубьями пильного цилиндра, которая влияет на величину силы отрыва. В работе [3] предложена «пружинная» модель для описания распределения давления в зоне контакта, где зависимость величиной углубления зубья пилы в сырцовом валике и нормальной силы принята по линейному закону. В этой работе не рассматриваются вопросы возникновения зоны скольжения в области контакта и оценка ее влияние на величину силы отрыва. В ней изучено качение абсолютно жесткого катка по релаксирующей среде и возникновение силы трения. При этом объяснено несимметричное распределение силы давления катка на среду по поверхности контакта. В данной работе изучено влияние скорости вращения валика и угла отклонения линии, соединяющей центры валика и пильного цилиндра от вертикали, на контактную силу взаимодействия сырцового валика с пильным цилиндром. Пусть сырцовый валик, моделируемый деформируемым цилиндрическим телом радиуса ![]() , катится без скольжения с постоянной линейной скоростью
, катится без скольжения с постоянной линейной скоростью ![]() по вращающемуся пильному цилиндру. Радиус и линейную скорость цилиндра обозначим соответственно
по вращающемуся пильному цилиндру. Радиус и линейную скорость цилиндра обозначим соответственно ![]() и
и ![]() . В стационарном состоянии процесса взаимодействия сырцового валика с цилиндром, все силы, действующие на сырцовый валик, уравновешиваются. Перечислим эти силы (рис.1):
. В стационарном состоянии процесса взаимодействия сырцового валика с цилиндром, все силы, действующие на сырцовый валик, уравновешиваются. Перечислим эти силы (рис.1):
1.Силы, извне приложенные к валику (включая силу тяжести), которые, будучи, приведенные к геометрическому центру валика, образуют пару моментом ![]() , горизонтальную силу
, горизонтальную силу ![]() и вертикальную силу
и вертикальную силу ![]() .
.
2.Сила сцепления сырцового валика с цилиндром, удерживающая валик от скольжения и обусловленная в зоне контакта внедрением зубьев пильного цилиндра в сырцовом валике и отрывом волокон от семян.
3.Распределенная по поверхности нормальная сила контакта. Удельное давление ![]() , производимое этими силами, будем считать постоянным вдоль образующих цилиндрической поверхности сырцового валика.
, производимое этими силами, будем считать постоянным вдоль образующих цилиндрической поверхности сырцового валика.
Направим ось ![]() вдоль линии контакта, обозначим через
вдоль линии контакта, обозначим через ![]() и
и ![]() соответственно координаты начала и конца соприкосновения пильного цилиндра с сырцовым валиком. Условия равновесия сил, приложенных к пильному цилиндру (ведомое колесо), имеют вид
соответственно координаты начала и конца соприкосновения пильного цилиндра с сырцовым валиком. Условия равновесия сил, приложенных к пильному цилиндру (ведомое колесо), имеют вид
![]() (1)
(1)
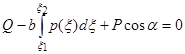 (2)
(2)
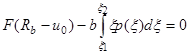 (3)
(3)
где ![]() сила веса сырцового валика,
сила веса сырцового валика, ![]() - ширина валика,
- ширина валика, ![]() - величина приближения центров пильчатого барабана и сырцового валика
- величина приближения центров пильчатого барабана и сырцового валика
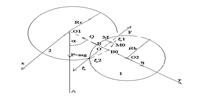
Рис.1 Схема распределения сил в зоне контакта ![]() пильного цилиндра 1 с сырцовым валиком 2.
пильного цилиндра 1 с сырцовым валиком 2.
Для осуществления контакта сырцового валика с пильным цилиндром без проскальзывания необходимо требовать выполнения неравенства
![]()
где ![]() - коэффициент трения скольжения поверхности пильного цилиндра по поверхности сырцового валика. Иначе возникает проскальзывание, и эффективность отделения волокна от семян снижается. При вдавливании пильного цилиндра в сырцовый валик его самая отдаленная точка
- коэффициент трения скольжения поверхности пильного цилиндра по поверхности сырцового валика. Иначе возникает проскальзывание, и эффективность отделения волокна от семян снижается. При вдавливании пильного цилиндра в сырцовый валик его самая отдаленная точка ![]() внедряется в деформируемый валик на глубину
внедряется в деформируемый валик на глубину ![]() . Найдем величину углубления пильного цилиндра в некоторой другой точке
. Найдем величину углубления пильного цилиндра в некоторой другой точке ![]() валика. Запишем в системе координат
валика. Запишем в системе координат ![]() уравнения окружностей с центрами в точках
уравнения окружностей с центрами в точках ![]() и
и ![]()
![]() ,
, ![]()
Величина углубления пильного цилиндра будет равна
![]() (4)
(4)
С точностью до малых четвертого порядка (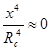 ,
, 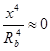 ) имеем
) имеем
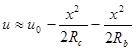 или полагая
или полагая ![]() , получаем
, получаем
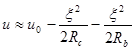 (5)
(5)
Вводим подвижную систему координат ![]() . Эта система координат перемещается с линейной скоростью
. Эта система координат перемещается с линейной скоростью ![]() вправо, абсцисса точки
вправо, абсцисса точки ![]() с течением времени уменьшается и поэтому
с течением времени уменьшается и поэтому ![]() . В начале соприкосновения пильного цилиндра с валиком (
. В начале соприкосновения пильного цилиндра с валиком (![]() ) величина углубления равна нулю, и, следовательно, согласно (5) имеем
) величина углубления равна нулю, и, следовательно, согласно (5) имеем
![]() (6)
(6)
Откуда ![]() можно выразить через
можно выразить через ![]() (
(![]() ),
), ![]()
Для определения удельного давления используем «пружинную» модель [3] согласно которой давление в зоне контакта пропорционально величине углубления, т.е
![]()
Равнодействующая сила давления на сырцовый валик и момент трения согласно (2) и (3) определяются формулами ![]()
![]()
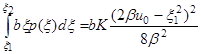
Подставляя выражения для ![]() и
и ![]() в формулах (2) и (3), получаем
в формулах (2) и (3), получаем
![]()
![]() (7)
(7)
![]()
![]() (8)
(8)
Уравнения (7) и (8) при заданных величинах сил ![]() ,
,![]() и угла
и угла ![]() образуют систему нелинейных уравнений для определения перемещения
образуют систему нелинейных уравнений для определения перемещения ![]() и координаты
и координаты ![]() . Исключив
. Исключив ![]() из этой системы, установлено трансцендентное уравнение для определения перемещения
из этой системы, установлено трансцендентное уравнение для определения перемещения ![]() .
.
Кроме того составлено выражение кинетической энергии сырцового валика при контакте с пильным цилиндром, где учитывается сила давления и сила трения. По принципу Лагранжа составлена динамическая система уравнения, описывающая характер взаимодействия сырцового валика с пильным цилиндром. В результате решения системы уравнений получены зависимости силы контакта между сырцовым валиком и пильным цилиндром.

