Одной из основных задач развития математического образования в Российской Федерации является формирование у учащихся прикладных умений, в том числе – умений использовать математический подход в рассуждении, обосновании, аргументации, планировании, в пространственных построениях, численных оценках. Согласно Концепции развития математического образования в РФ (далее – Концепция; см. [1]), «изучение и преподавание математики, с одной стороны, обеспечивают готовность учащихся к применению математики в других областях, с другой стороны, имеют системообразующую функцию, существенно влияют на интеллектуальную готовность школьников и студентов к обучению, а также на содержание и преподавание других предметов».
В соответствии с задачами, поставленными Концепцией, в настоящей работе обсуждаются вопросы формирования у учащихся старшей школы компетенции математического моделирования. А именно:
– сформулировано понятие данной компетенции и выделены ее основные компоненты;
– приведена классификация моделей, используемых в процессе обучения в старшей школе и рассмотрены вопросы «внутриматематического» моделирования;
– предложено структурирование компетенции на уровни и показатели их освоения.
1. Компетенция математического моделирования введена в педагогическую науку сравнительно недавно (см. напр., [5]). Применительно к процессу обучения в старшей школе её можно определить как способность актуализировать и применять математические знания и умения при построении, анализе и интерпретации математических моделей в процессе решения задач как учебных, так и практических.
Выделим следующие компоненты данной компетенции.
1.1. Мотивационно-ценностный компонент. Мотив рождается вместе с пониманием универсальности математического языка, необходимости формализации законов физики, химии, биологии, экономики. Изучая данные и другие дисциплины, учащийся приходит к убеждению, что математические методы выступают в качестве инструмента исследований в различных областях деятельности, при разработке, анализе и принятии решений, в силу чего освоение математических дисциплин должно стать осознанной целью и подлежит включению в личностный смысловой контекст его деятельности.
1.2. Кругозор и постоянное его расширение – необходимый компонент компетенции математического моделирования. Речь идет не только об освоении содержания учебных дисциплин, но и постоянном росте культурного уровня учащегося. Расширение кругозора неизбежно сопровождается анализом явлений и процессов, сравнительными характеристиками, логическими умозаключениями и т.п. В свою очередь, указанные формы мыслительной деятельности способствуют развитию метапредметных умений выделять главное и отбрасывать второстепенное, кратко и ясно выражать свои мысли, ставить задачи, получать и четко формулировать выводы, а эти умения успешно «встраиваются» в процессы математического моделирования.
1.3. Знания и умения. Речь идет об актуализации предметных знаний и умений как математических, так из смежных областей, применительно к выстраиваемой модели, а также о коммуникативных умениях (использование языка математики в речи и в письме, построение графиков, схем, диаграмм и др.) и умении применять в процессе моделирования современные информационные технологии.
1.4. Опыт деятельности в области моделирования способствует переносу математических знаний и умений на незнакомые ситуации, в том числе, возникающие в практической деятельности.
1.5. Наконец, рефлексия является важнейшим компонентом соответствующей компетенции и способствует развитию таких качеств учащегося, как самоконтроль, ответственность, рациональность, самостоятельность.
2. Классификация моделей. В работе [3] предложены следующие четыре класса моделей, используемых в процессе решения задач межпредметной и практико-ориентированной направленности.
1) Модели формально-логического типа: здесь имеет место формализация рассуждений средствами логики высказываний и предикатов.
2) Аналитические модели: здесь процессы функционирования реальных объектов, или систем записываются в виде явных функциональных зависимостей. При этом мы выделяем:
– модели-преобразования, модели-уравнения (алгебраические, трансцендентные, дифференциальные) и модели – неравенства;
– модели-аппроксимации и модели-оптимизации (задачи интерполяции, экстраполяции, численное интегрирование, численные методы решения простейших дифференциальных уравнений, задачи максимизации и минимизации линейных форм и др.).
3) Геометрические модели, использующие плоские и пространственные геометрические объекты.
4) Вероятностно-статистические модели (вероятностные характеристики случайных событий, анализ статистических данных и их статистическая обработка).
5) Модели смешанного типа. Так, например, ситуации, моделируемые в форме задач стереометрии, которые могут быть решены векторно-координатным методом, используют, по сути, как аналитический, так и геометрический аппарат; задачи на нахождение вероятностей случайных событий предполагают использование логических операций (здесь общей основой являются булевы алгебры; см. [2]); при нахождении числовых характеристик случайных величин задействован аналитический аппарат.
3. «Внутрипредметное» моделирование. Опираясь на концепцию А.А. Ляпунова (см. напр. [4]), внутрипредметное («внутриматематическое») моделирование будем понимать как опосредованное теоретическое исследование математического объекта (напр., доказываемого утверждения, решаемой задачи и др.) путем его замещения моделью одного из вышеперечисленных типов, с целью получения (вследствие «внутримодельного» решения) необходимого результата для самого моделируемого объекта. Процесс внутриматематического моделирования способствует формированию представлений о системности математических приемов и методов, расширяет спектр используемых учащимся инструментов решения задач. Так, решение планиметрических и стереометрических задач во многом облегчается привлечением аналитических моделей (введение неизвестных – ограничения на их значения – установление связей между известными и неизвестными величинами – составление уравнения или системы уравнений и получение соответствующего решения в рамках аналитической модели – геометрическая интерпретация). В свою очередь, решения задач алгебры или анализа во многом проясняются при использовании моделей формально-логического типа (уравнения-следствия, равносильные уравнения как, соответственно, следствия предикатов и равносильные предикаты; системы неравенств как конъюнкции, совокупности неравенств – как дизъюнкции предикатов и др.).
Далее, некоторые алгебраические задачи повышенной и высокой сложности (например, задачи с параметрами) могут быть решены средствами геометрического моделирования. Примером может служить следующее задание.
Найти все значения параметра а, при которых система уравнений
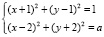
имеет единственное решение.
Стандартным приёмам решения (методы подстановки или алгебраического сложения) здесь стоит предпочесть рассмотрение соответствующей геометрической модели, а именно ситуаций внешнего и внутреннего касания двух окружностей (система записана в виде их уравнений), после чего параметр а определяется путем применения теоремы Пифагора.
4. Для уточнения результатов освоения компетенции математического моделирования в терминах «знать, уметь, владеть» будем использовать так называемый паспорт компетенции. Он включает в себя совокупность требований Федерального государственного стандарта к уровню сформированности компетенции по окончании освоения образовательной программы (ООП), уточнение компонент содержания компетенции, структурирование компетенции на уровни и показатели.
4.1. Место и значимость компетенции математического моделирования в совокупном ожидаемом результате образования выпускника школы. Формирование данной компетенции является важным фактором подготовки выпускника к выполнению следующих видов учебной и практической деятельности:
– анализ понятий, фактов, ситуаций из различных предметных областей с использованием логических выводов, математического языка и методов математики и получение, вследствие этого, необходимой информации в рамках соответствующей предметной области и практических рекомендаций при решении прикладных задач;
– интерполяция и экстраполяция результатов;
– выдвижение гипотез и их проверка средствами вероятностно-статистической теории.
4.2. Компоненты содержания компетенции, подлежащие оцениванию по освоении ООП:
– предметный – теоретическая основа компетенции математического моделирования, включающая в себя математические знания и умения, а также соответствующие способы действия;
– собственно модельный, предусматривающий пошаговое выполнение алгоритма моделирования;
– вычислительный – решение задач с конкретными числовыми значениями величин;
– прогностический – направленный на выяснение тенденций развития состояний исследуемого явления или объекта в рамках детерминированной или вероятностной модели.
4.2. Результаты обучения, раскрывающие структуру компетенции и планируемые уровни ее сформированности. Мы выделяем три следующих основных уровня.
1) Пороговый уровень, как минимально необходимый для всех выпускников старшей школы по завершении освоения ООП и достаточный для самостоятельного анализа простейших математических моделей. Работа же с более сложными моделями может быть осуществлена под руководством учителя.
2) Базовый уровень, позволяющий решать типовые задачи, использовать известные алгоритмы, правила и методики как в процессе решения собственно математических задач, так и на этапах математического моделирования. Речь идет, по сути, о соответствии требованиям к результатам освоения ООП среднего (полного) общего образования в области математики на базовом уровне.
3) Продвинутый уровень – максимально возможная выраженность компетенции. Здесь речь идет о соответствии достигнутых результатов требованиям к результатам освоения ООП среднего (полного) общего образования в области математики на профильном и углубленном уровнях.
Перечислим основные (по нашему мнению) признаки каждого из перечисленных уровней.
На пороговом уровне учащемуся необходимо
– знать: основные формулы алгебры и тригонометрии; определения и графики основных элементарных функций; формулировки понятий и фактов геометрии, необходимых для решения простейших планиметрических и стереометрических задач; понятия и факты из математического анализа, необходимые для исследования функциональных зависимостей; элементарные положения теории вероятностей и математической статистики;
– уметь: выполнять стандартные алгебраические и тригонометрические преобразования и решать простейшие алгебраические и трансцендентные уравнения; визуализировать данные в виде геометрических объектов; вычислять производные и интегралы на основе табличных формул; извлекать информацию, представленную в таблицах, на диаграммах, графиках;
– владеть: методами геометрической интерпретации простейших задач на определение взаимного расположения объектов и нахождения их размеров и таких числовых характеристик как площади или объемы; методами дифференциально-интегрального исчисления в простейших случаях исследования моделей (например, вычисление скорости, площади, работы переменной силы и т.п.); способами систематизации статистических данных в виде рядов распределения, полигонов и гистограмм.
На базовом уровне учащийся должен
– знать: в полном объеме используемые в школьном курсе математики формулы алгебры и тригонометрии, функциональные понятия и их графические интерпретации, а также понятия и факты геометрии; положения дифференциально-интегрального исчисления, необходимые для исследования функций и нахождения геометрических и физических величин; основные понятия, вероятностные схемы и формулы теории случайных событий, а также понятия и факты, связанные с анализом эмпирических распределений;
– уметь: проводить доказательства основных известных (из школьного курса) математических утверждений; использовать функционально-графические представления для решения как математических, так и практико-ориентированных задач; получать информацию о количественных характеристиках предметов окружающего мира на основе фактов геометрии; систематизировать массивы числовых данных и определять их статистические характеристики, использовать вероятностные методы при принятии решений в ситуациях неопределенности;
– владеть: вычислительными навыками; символьным языком и методами алгебры, тригонометрии, геометрии при формализации и решении задач из смежных областей и практико-ориентированных задач; системой функциональных понятий и фактов для описания и анализа реальных зависимостей; способами построения и изучения простейших вероятностных моделей и получении информации о теоретических распределениях на основе выборочных данных.
На продвинутом уровне предполагается, что учащийся, в дополнение к знаниям, освоенным на базовом уровне, обладает первичными знаниями аналитической геометрии, комплексного анализа, теории многочленов, простейших дифференциальных уравнений, а также умеет комбинировать известные ему методы доказательств при обосновании новых утверждений, переносить освоенные приемы решения задач на новые, в том числе, практические ситуации.
Продвинутый уровень предполагает, что учащийся владеет: специальными приемами решения задач повышенной сложности (напр., задач с параметрами и др.); векторно-координатным методом (в дополнение к стандартным геометрическим методам); расширенным алгоритмом исследования функциональных зависимостей (включая асимптотическое поведение функций, характер выпуклости и др.) и специальными приемами интегрирования отдельных классов функций; стандартными распределениями случайных величин и методами получения точечных и интервальных оценок параметров теоретических распределений.
Приведем примеры задач, использующих геометрические модели, которые соответствуют достигнутому учащимся уровню.
Пороговый уровень. На сколько увеличится площадь прямоугольного земельного участка, имеющего периметр, равный 32 м, если каждую сторону прямоугольника увеличить на 4 метра?
Базовый уровень. При каких размерах прямоугольного участка заданного периметра его площадь будет наибольшей?
Продвинутый уровень. Из круглого бревна с заданным диаметром поперечного сечения вытесывается балка с прямоугольным поперечным сечением. Каковы должны быть его размеры х и у, чтобы прочность балки была наибольшей, если прочность пропорциональна xy2?
Заключение
Как следует из вышеизложенных положений, формирования компетенции математического моделирования порождает следующие непосредственные и опосредованные результаты.
1. Постановка задачи моделирования процессов и явлений служит мотивом для введения новых понятий и расширения арсенала используемых математических фактов и методов.
2. На этапе решения задачи внутриматематическое моделирование выступает дополнительным средством для решения собственно математических задач.
3. На этапе интерпретации результата моделирование служит источником получения дополнительной информации об исследуемом объекте в терминах исходной предметной области.
Таким образом, формирование у учащихся «модельного взгляда» на задачи из смежных областей, практико-ориентированные и собственно математические задачи, отвечает требованиям, предъявляемым Концепцией к системе математического образования и расширяет возможности развития самой этой системы.

