Для краткосрочного прогнозирования тренд-сезонных временных рядов можно использовать адаптивные модели с сезонной компонентой, например, модель Хольта-Уинтерса. Мультипликативная модель Хольта-Уинтерса с линейным ростом имеет вид:
Yp(t + k) = [a(t) + k b(t)] F(t + k – L), (1)
где k – период упреждения; Y(t) – расчетное значение экономического показателя для t-го периода; a(t), b(t) и F(t) – коэффициенты модели; L – период сезонности (для квартальных данных L = 4, для месячных L = 12). F(t + k – L) является значением коэффициента сезонности того периода, для которого рассчитывается экономический показатель. Очевидно, что для малых значений t аргумент функции F будет отрицательным.
Уточнение коэффициентов модели проводится по формулам:
a(t) = α1Y(t)/F(t – L) + (1 – α1) [a(t – 1) + + b(t – 1)]; (2)
b(t) = α3[a(t) – a(t – 1)] + (1 – α3)b(t – 1); (3)
F(t) = α2Y(t)/a(t) + (1 – α2)F(t – L). (4)
Алгоритм вычислений следующий [3].
Для оценки начальных значений a(0) и b(0) применяют линейную модель метода наименьших квадратов (МНК) к первым членам ряда. Значения коэффициентов сезонности для отрицательных значений аргумента рассчитываются как среднее арифметическое за несколько соответствующих периодов. Значения коэффициентов сезонности для положительных значений аргумента вычисляются по формуле (4).
Для значений t = 1 значения Yp вычисляются по формуле (1). Затем по формулам (2)–(4) вычисляется текущие значения всех параметров модели.
Прогнозируемые значения Yp рассчитываются по формуле (1) при фиксированном t и различных значениях k.
Данный алгоритм легко реализуется в электронных таблицах Excel, которые являются удобным инструментом для вычислений, когда данные представлены в табличной форме [1].
Очевидно, что наиболее сложным и нетривиальным пунктом данной модели является подбор коэффициентов α1, α2, α3. Поскольку в уравнение (1) предыдущее значение показателя входит не явно, применение традиционных методик, таких как метод градиентного спуска или формализм нейронных сетей, является сложным и неудобным. Более подходящими являются различные модификации симплекс-метода [2]. Однако недостатком этого алгоритма является медленная сходимость и достаточно громоздкая программная реализация. Мы разработали простой, но достаточно эффективный алгоритм нахождения подходящих значений параметров a, в основе которого лежит минимизация часто применяющегося в теории нейронных сетей функционала
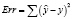 ,
,
где ? и y – модельные и табличные значения результирующего фактора соответственно.
Наши вычисления показали, что для различных наборов значений параметров a результаты моделирования могут практически не отличаться визуально и иметь близкие значения функционала Err. Таким образом, значения этих параметров не являются достаточно специфическими и не могут существенно отражать природу динамических процессов.

