Многочисленными исследованиями показано, что физиологическое и психическое состояния человека подвержены модуляциям внешних природных циклических процессов на внутренние биоритмы организма с учетом экологической нагрузки [1,8]. Методика учета биоритмов при оказании терапевтических воздействий в процессе лечения к настоящему времени достаточно освоена в хрономедицине [6]. Между тем, в педагогике эти вопросы практически не рассматриваются (за исключением воспитания спортсменов), несмотря на то, что индивидуальное физическое и психическое развитие организма по мере взросления безусловно имеет ритмическую составляющую как у здоровых людей, так и у имеющих психические отклонения различной степени тяжести.
Освоение новых знаний, приобретение навыков и умений согласно стандартам и-или индивидуальным планам безусловно связано с психическим состоянием обучающегося, особенно у больных людей. Это проявляется в коллективе, где присутствуют люди – ученики и учителя – различной возрастной категории, различными биоритмилогическими особенностями, индивидуальной толерантностью по отношению к изменениям (в том числе и обладающими ритмическими особенностями) окружающей среды.
Таким образом представляется актуальным разработка системы выявления психических биоритмов обучающихся для оптимизации процесса улучшения качественных показателей приобретения новых знаний и навыков людьми с психическими расстройствами путем синхронизации ритмики обучения с биоритмами человека.
Материалы и методы исследования
Методы исследования основываются на математической статистике, самоорганизационного математического моделирования, выявление и анализ ритмических составляющих, модулируемых экзозогенными природными циклами.
Результаты исследования и их обсуждение
Процесс обучения определяется не только желанием учиться (целевая установка обучающегося) и качеством преподавания (внешним воздействием), но и состоянием организма обучающегося с необходимым качеством восприятия новых знаний. Поскольку процесс обучения во многом определяется психологией преподования и психическим состоянием личности обучаемого, то немаловажным фактором обучения является обеспечение согласования характеристик ритмичности педагогического процесса с биоритмами автономного искусственного интеллекта (и соответствующему автономному процессу управления) [2].
Стандартный (классический) педагогический процесс в силу его целевого формирования для решения образовательных задач государственного уровня рассчитан на некоторый «усредненный» уровень, не предполагающий психические отклонения состояния обучаемого. В настоящее время доказано, что психика человека во многом подчинена внешним модуляциям внешних природных циклов на внутренние (генетически обусловленные и-или приобретенные) биоритмы функционирования различных функциональных систем организма (особенно связанных с проявлением высшей нервной деятельности).
Это сказывается на организмах, имеющих какие-либо психические отклонения (в том числе вызванные патологией физиологических систем), поскольку они обладают меньшей степенью толерантности к внешним воздействиям. К наиболее встречающимся психическим отклонениям (заболеваниям) взрослых и детей относятся шизофрения, умственная отсталость и иные психические расстройства, идентифицируемые медициной. Психозы – группа наиболее тяжелых (для личности и общества) психических болезней, сопровождающихся выраженными расстройствами психической деятельности, галлюцинациями, помрачением сознания, резкими двигательными и аффективными расстройствами и др. Проявляется преимущественно неадекватным отражением реального мира с нарушением поведения. Шизофрения – эндогенная психическая болезнь с непрерывным или приступообразным течением, проявляющаяся изменением личности и продуктивными синдромами. Умственная отсталость – стойко выраженное снижение познавательной деятельности, возникающее на основе органического поражения центральной нервной системы. Причины возникновения носят эндогенный и экзогенный характеры.
Знание характера и динамики поведения организма позволяет организовывать процесс обучения с учетом ритмичности заболеваний, путем синхронизации ритмов обучения и аутобиоритмов обучающегося на основе прогнозирования состояния последнего во много подчиненного природным циклическим воздействиям, которые в настоящее время достаточно точно идентифицированы и дифференцированы.
Ритмическим особенностям психических расстройств посвящено достаточно много исследований (например, [3, 7]), не учитывающих, как правило, влияния иных внешних факторов окружающей среды, носящих региональный характер.
Поскольку учесть все разнообразие экологических факторов, вносящих разнообразие в ритмы психических заболеваний не представляется возможным (в том числе, в силу их многообразия и изменчивости), то можно предположить, что их влияние сказывается на параметрах математических моделей, отражающих циклические изменения анализируемых заболеваний.
В связи с этим, предлагается синтезировать математические модели для каждого региона отдельно по схеме, представленной на рисунке. Предлагаемая на схеме технология структурно-параметрического моделирования совмещает в себе достоинства системного подхода, регрессионного, корреляционного анализов и самоорганизационной концепции моделирования в априорно не детерминированном классе моделей.
На первом этапе исследователь формирует пространства факторов (и отклика характеристики проявления психических отклонений.
На втором этапе осуществляется начальный статистический, корреляционный и регрессионный анализы с целью возможного сужения пространства отклика путем идентификации высокозначимых линейных и нелинейных взаимосвязей и исключения, впоследствии, таковых из дальнейшего рассмотрения как функционально взаимосвязанных. Полученные на данном этапе первичные модели позволяют использовать информацию о существующих внутренних взаимосвязях и на последнем этапе – принятие управленческих решений, т.к. позволяют прогнозировать внутреннюю структуру пространства отклика, предположить и идентифицировать внутренние системные функциональные отношения.
На третьем этапе – в блоке «выделение текущего тренда» – для каждого отклика i идентифицируются l1 лучших моделей следующим образом. Рассматриваются различные варианты сглаживания исходной информации (рекомендуются сглаживание по 3, 5 и 7 точкам) и различные варианты временного сдвига (рекомендуются не более чем на половину от общего времени сбора мониторинговой информации). Для каждого варианта идентифицируются модели регрессионных структур (например, представленных в табл. 1. По критерию детерминации отбирается l1 лучших моделей для дальнейшего анализа.
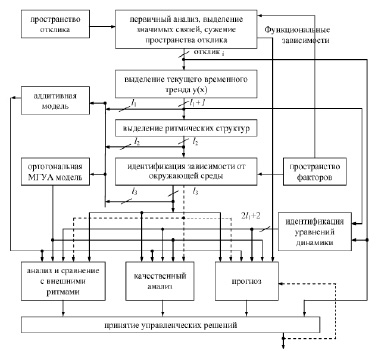
Технология математического моделирования
На четвертом этапе осуществляется выделение возможных ритмических структур. При этом в качестве исходного временного ряда рассматривается (l1+1) – вариант: непосредственно отклик i и l1 – варианты удаления из него векторов значений функций отклика полученных ранее математических моделей. Выделение ритмических структур осуществляется:
– амплитудной модуляцией
А0+∑Аisin(ωit+ϕi);
– амплитудно-детекторнаой модуляцией
А0+∑Аi[sin(ωit+ϕi)];
– фазочастотной модуляцией
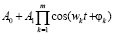, m=2, 3;
негармонические ритмические структуры, где А0 – начальное смещение; А1 – коэффициент при терме, ω – круговая частота колебаний, φ – фаза колебаний.
Для структурно-параметрической идентификации предлагаемых моделей рекомендуется примется применять метод группового учета аргументов, позволяющий:
- выявлять некратные гармоники, что приближенно к естеству, поскольку априори отсутствует базовая частота зависящая от мощности выборки;
- адекватно работать с маломощными выборками, чего не скажешь, например, о спектральном анализе;
- наиболее приближен к самоорганизации в живом мире и общей самоорганизационной предлагаемой технологии моделирования.
Затем отбираются l3 наилучшие модели описанным ранее способом. На данном этапе возможно возникновение варианта, когда исследователя интересует не только l3 лучших моделей, но и модели отражающие связь отклика с другими факторами окружающей среды в случае ее статистической значимости. В связи с этим, запоминаются все значимые модели, и их структура и параметры по желанию исследователя могут быть использованы при анализе и прогнозе. На рисунке эта связь показана пунктиром.
Таблица 1
Регрессионные структуры
|
Структура модели y(t) T∈[1,+∝) |
Прямое преобразование к линейной регрессии Z=f(b0,b1,x) |
Обратное преобразование (восстановление параметров модели) |
|
a0+a1t |
x=t; z=y |
a0=b0; a1=b1 |
|
a0+a1t+a2t2 |
k1=t; x2=t2; z=y |
a0=b0; a1=b1; a2=b2 |
|
a0+a1t+a2t2+a3t3 |
x1=t; x2=t2; x3=t3 |
a0=b0; a1=b1; a2=b2 |
|
a0+a1logct, c={2, 3, e, p, 10} |
x=ln(t); z=y |
a0=b0; a1=b1/logce |
|
1/(a0+a1t) |
x=t; z=1/y |
a0=b0; a1=b1 |
|
a0(c)a1/t, c={2, 3, e, p, 10} |
x=1/t; z=ln(y) |
a0=exp(b0); a1=b1/ln(c) |
|
a0(c)-a1/t , c={2, 3, e, p, 10} |
x=–1/t; z=ln(y) |
a0=exp(b0); a1=b1/ln(c) |
|
a0(c)a1t , c={2, 3, e, p, 10} |
x=t; z=ln(y) |
a0=exp(b0); a1=b1/ln(c) |
|
a0(c)-a1t , c={2, 3, e, p, 10} |
x=-t; z=ln(y) |
a0=exp(b0); a1=b1/ln(c) |
|
a0/(a1+t) |
x=t; z=1/y |
a0=1/b1; a1=a0b0 |
|
a0/(a1–t) |
x=-t; z=1/y |
a0=1/b1; a1=a0b0 |
|
a0t/(a1+t) |
x=1/t; z=1/y |
a0=1/b0; a1=a0b1 |
|
a0t/(a1–t) |
x=1/t; z=1/y |
a0=–1/b0; a1=a0b1 |
|
1/(a0+a1ct), c={2, 3, e, π} |
x=сt; z=1/y |
a0=b0; a1=b1 |
|
1/(a0+a1*c-t), c={2, 3, e, π} |
x=с-t; z=1/y |
a0=b0; a1=b1 |
|
a0+a1/t |
x=1/t; z=y |
a0=b0; a1=b1 |
|
a0c-t /(a1+с-t), c={2, 3, e, π} |
x=1/e-t; z=1/y |
a0=1/b0; a1=a0⋅b1 |
|
a0ct /(a1–сt), c={2, 3, e, π} |
x=1/сt; z=1/y |
a0=–1/b0; a1=a0⋅b1 |
|
t/(a0+a1t) |
x=1/t; z=1/y |
a0=b0; a1=b1 |
|
a0a1t |
x=t; z=ln(y) |
a0=exp(b0); a1=exp(b1) |
На данном этапе отбирается l2 лучшие модели аналогично описанному ранее способу предыдущего этапа.
Далее, из полученных l1, l2 и l3 моделей выделяются их структуры (без параметров, отражающих линейное перемещение), которые используются в соответствующих блоках идентификации аддитивной и ортогональной моделях второго уровня, следующего вида:
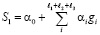, (1)
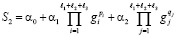. (2)
где gi – структура i-й модели из множества l1+l2+l3.
(Структура (2) идентифицируется ортогональным алгоритмом метода группового учета аргументов [5], (1) – алгоритм множественного линейного регрессионного анализа с исключением переменных [4]).
Таким образом, после окончания данного этапа исследователь имеет (l3+2) модели для дальнейшего анализа.
Параллельно алгебраическому моделированию осуществляется анализ временного ряда рассматриваемого отклика путем поиска дифференциального уравнения динамики (функция Бесселя и уравнение второго порядка). Синтез уравнений предлагается осуществлять как на базе «чистого» временного ряда отклика, так и после удаления из него l1 временных трендов.
В результате, общее количество синтезированных на последних этапах предлагаемой технологии моделей равно (l3+2+2l1+2)=2l1+l3+4.
Дальнейшее исследование предполагает три этапа:
1) анализ и сравнение с внешними ритмами – в этом случае осуществляется сравнение с базой данных основных внешних ритмов: солнечных, лунных и космических. Это делается с целью поиска возможного внешнего синхронизатора или, по крайней мере «норматива», «маркера» идентифицированных колебаний.
2) качественный анализ – осуществляется описание исследуемых моделей на предмет гносеологического описания системных связей и выявления управляемых факторов и их компенсирующего влияния.
3) прогноз – осуществляется прогнозирование динамики одного или множества откликов с учетом возможного изменения ситуации в окружающей среде. На данном этапе используется информация о зависимостях откликов между собой. Рекомендуется рассматривать три вида прогноза: два экстремальных (наихудший и наилучший) и наиболее вероятный.
Исследования психических отклонений людей в Курской области позволили выявить следующее.
Для психозов наиболее характерна ритмическая составляющая в совокупности с экспоненциально возрастающим (константа π) временным трендом. При этом, гармоническая часть представляет собой амплитудно-частотную модуляцию двух синусоидальных функций с периодами 10 и 6,5 лет (что наиболее близко к циклам солнечной и геомагнитной активностей, соответственно) и фазовыми сдвигами 0,9 и 5,8 лет (что соответствует периодичности вращения Земли вокруг Солнца и изменениям скорости суточного вращения Земли, соответственно).
Для шизофрении наиболее характерна трех частотная амплитудная модуляция с периодами 50, 5,8 и 3 лет (4-кратный период изменения скорости суточного вращения Солнца, первый базовый период изменения скорости суточного вращения Земли, полупериод геомагнитной активности) с фазовыми сдвигами соответственно – 2,3, 3,4 и 0,6 лет; и одночастотная ритмическая составляющая с периодичностью в 18 лет (одна десятая составляющая периодичности интенсивности числа Вольфа на Солнце) на фоне кубического временного тренда.
В моделях отражающих динамику людей с психическими расстройствами наблюдается двухчастотный модулируемый ритм на фоне кубического временного тренда с периодами в 18 и 3,3 лет (одна десятая часть цикла изменения числа Вольфа на Солнце и третий базовый период изменения скорости суточного вращения Земли) со сдвигом фаз 9,9 и 5,6 лет, соответственно.
Динамика исследуемого умственной отсталости также подчиняется гармоническому закону с амплитудной модуляцией по четырем частотам, которым соответствуют периоды 26,2, 6,1, 3,7 и 2,3 лет (что соответствует 6-ти кратному периоду колебаний геомагнитной активности, изменению уровня Ar на Солнце, периоду и полупериоду данного изменения и его трети) и фазовым сдвигом в 0,5, 3,2, 1,4 и 1,4 года, соответственно.
Таким образом, результаты исследований подтвердили факт подчинения ритмики психических отклонений циклам Солнечной активности и Земным составляющим (геомагнитной напряженности и изменениям скорости суточного вращения нашей планеты) с учетом региональной особенности (в Курской области существено повышен уровень естественного геомагнитного поля).
Выводы и рекомендации
С учетом выявленных циклов рекомендуется формировать ритмику учебного процесса, учитывающего:
– «длинные ритмы» (длительностью не менее 3-4 месяцев): программа обучения учитывает сезонные колебания (в основном полугодовые или годовые) следующем образом: с помощью определенного теста анализируется текущее состояние обучающегося и, зная его психическое заболевание (отклонение) и ему соответствующий доминирующий ритм осуществляется коррекция нагрузки освоения определенной образовательной траектории (здесь, очевидно, необходимо оптимизировать учебные планы направлений обучения в целом);
– «средние ритмы» – периодичностью от 0,25 до 3 месяцев – учитывающие особенности реакции психики обучающегося на процесс обучения по рабочей учебной программе конкретной дисциплины (учебное понедельное планирование);
– «короткие ритмы» – периодичностью от частей суток до нескольких суток, к каковым относятся, например: максимальная чувствительность пальцев (15–16 ч.), максимальная работоспособность легких (16–18 ч.), максимальная активность мозга (10–12 ч.) и т.п. Эти ритмы необходимо учитывать при индивидуальном обучении и «поурочном планировании» с учетом времени суток, фото-, термо- и звуковых обстановок обучения.
Проведенные исследования подтверждают необходимость систематизации знаний в рассматриваемой предметной области и формирования фундаментальных и прикладных знаний, – по сути: формирования направления хронопедагогики.