Совершенствование системы государственной итоговой аттестации, завершающей освоение основных образовательных программ основного общего и среднего образования, привело к появлению кодификаторов элементов содержания и требований к уровню подготовки выпускников общеобразовательных учреждений. «Моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий» – одно из требований кодификатора при сдаче Единого Государственного Экзамена в 2016 году [6].
Федеральный компонент Государственного стандарта общего образования обязывает знакомство учащихся с понятием частоты события, формирование представлений о равновозможных событиях и способах подсчета их вероятностей, изучение геометрической вероятности. Таким образом, необходимым и важным компонентом математического образования в школе является изучение элементов теории вероятностей. Необходимым компонентом предмета теории вероятностей является знакомство с классическим определением вероятности в 7 классе общеобразовательной школы.
Одно из базовых понятий теории вероятностей – это событие. Событием называется «возможный результат испытания (опыта)» [2]. События бывают достоверными, невозможными и случайными. Событие называют достоверным, если «в результате данного испытания оно обязательно произойдет» [3]. Например, событие «в условиях земного тяготения подброшенная монета непременно упадёт вниз» – достоверное. Событие называют невозможным , «если результате испытания оно вообще не может произойти» [3]. Пример невозможного события: «в условиях земного тяготения подброшенная монета улетит вверх». И, наконец, событие называется случайным в данном испытании, если «оно может произойти, а может и не произойти в этом опыте» [2]. Например, событие «в результате броска игрального кубика выпадет число 6» является случайным. При этом имеет место критерий случайности, по которому случайное событие есть следствие случайных факторов, воздействие которых предугадать невозможно или крайне затруднительно. В опыте с монетой случайные факторы – это форма и физические характеристики монеты, сила и направление броска, сопротивление воздуха и т.д.
В некотором смысле события можно разделить на два класса: «элементарные» события и «сложные» события [1]. Любой итог испытания называется элементарным исходом (элементарным событием или шансом) [2]. Например, при подбрасывании кубика возможны 6 элементарных исходов: «выпала цифра 1», «выпала цифра 2», ….. , «выпала цифра 6». Опыт с игральным кубиком имеет много других возможных результатов, которые шансами не являются. Например, событие «Выпало четное число» в данной терминологии является «сложным» событием.
Другая важная характеристика событий – это их равновозможность. Несколько событий называют равновозможными, если «нет оснований полагать, что одно событие является более возможным, чем другие» [2]. Например, события: «выпадение цифры» и «выпадение герба» при броске монеты – равновозможные события.
События называются несовместными, если «наступление одного исключает наступление другого при одном и том же испытании» [3]. Например, события: «выпадение цифры» и «выпадение герба» при броске монеты – несовместные события. События называются совместными, если «появление одного из них не исключает появление другого в одном и том же испытании» [1]. Например, события: «из колоды карт извлечена карта масти трефи» и «из колоды карт извлечена дама» – совместные, поскольку наступление одного не исключает наступление другого в одном испытании.
Вероятность события – это центральное понятие теории вероятностей. Существует несколько подходов к её определению: классическое, геометрическое и статическое определения вероятности.
Остановимся на классическом определении вероятности, которое может найти широкое применение в решении задач ЕГЭ и ГИА. Вероятностью события А назовем «отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных, несовместных, единственно возможных исходов испытания» [2]:
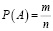 ,
,
где n – общее число всех равновозможных, несовместных, единственно возможных исходов этого испытания, m – количество благоприятствующих событию исходов.
Изучив материалы Открытых банков ЕГ и ГИА [4, 5, 6], мы выделили 3 типа задач на применение классического определения вероятности: I тип – задачи о классических опытах на кубиках, шарах и монетах; II тип – задачи о числах; и, наконец, III тип – разные задачи. Рассмотрим последовательно задачи всех типов.
I тип
Пример 1. В урне 10 одинаковых по размерам и весу шаров, из которых 4 красных и 6 синих. Из урны извлекается один шар. Какова вероятность того, что извлеченный шар окажется синим?
Решение. Испытание состоит в однократном извлечении шара. Событие А – «извлеченный шар оказался синим». Данное испытание имеет 10 равновозможных, несовместных, единственно возможных исходов (извлечение каждого отдельного шара и есть элементарный исход), из которых 6 – благоприятствующих событию А исходов. В соответствии с формулой получаем P(A)=6/10=0,6.
Этот классический пример иллюстрирует использование определения вероятности. Около 30 % задач на вычисление вероятности в материалах Открытого банка ЕГЭ и ГИА решаются применением данной формулы. На месте шаров могут быть яблоки и груши, мальчики и девочки, выученные и невыученные билеты, бракованные и стандартные детали – принцип остается тем же.
Пример 2. Подбрасываются две симметричные монеты. Чему равна вероятность того, что на верхних сторонах обеих монет оказались цифры?
Решение. Испытание – подбрасывание двух монет. Событие А – «на верхней стороне каждой монеты оказалась цифра». В этом испытании 4 равновозможных элементарных исхода: (Г, Г), (Г, Ц), (Ц, Г), (Ц, Ц). (Запись (Г, Ц) означает, что на первой монете герб, на второй – цифра). Событию A благоприятствует один элементарный исход – (Ц, Ц). Поскольку m = 1, n = 4 , то P(A)=1/4=0,25.
В решении аналогичных задач можно использовать правило произведения для подсчета общего числа элементарных исходов. Если при одном бросании монеты возможных исходов 2, то для двух бросаний число исходов будет 2·2=4. Для трех бросаний общее число исходов найдем умножением 2·2·2=8, и т.д., … , для N бросаний число элементарных исходов будет равно 2N.
Пример 3. Подбрасывается два игральных кубика, отмечается число очков на верхней грани каждого кубика. Найти вероятность того, на обоих кубиках выпало одинаковое число очков.
Решение. Испытание состоит в подбрасывании двух игральных кубиков. Обозначим событие А – «на обоих кубиках выпало одинаковое число очков». Всего равновозможных элементарных исходов n=62=36. Выпишем благоприятствующие событию А исходы: (1;1), (2;2), (3;3), (4;4), (5;5), (6;6); m=6.
Искомая вероятность P(A)= 6/36=1/6.
II тип
Пример 4. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?
Решение. Испытание состоит в выборе числа из натуральных чисел от 0 до 9. Обозначим событие А – «Случайно выбрано чётное число». На клавиатуре телефона 10 цифр, из них 5 четных: 0, 2, 4, 6, 8. Поэтому вероятность того, что случайно будет нажата четная цифра, равна P(A)=5/10 = 0,5.
Пример 5. Из множества натуральных чисел от 10 до 19 наудачу выбирают одно число. Какова вероятность того, что оно делится на 3?
Решение. Испытание состоит в выборе числа из натуральных чисел от 10 до 19. Обозначим событие А – «Наудачу выбранное число делится на 3». Натуральных чисел от 10 до 19 десять, поэтому n = 10. Число благоприятствующих исходов m = 3 (только три числа делятся на три, это числа: 12, 15, 18). Следовательно, искомая вероятность равна P(A)=3/10 = 0,3.
Пример 6. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение. Испытание состоит в выборе числа из данного набора чисел. Обозначим событие А – «Команда России выбрала число 2». Количество элементарных исходов испытания равно количеству чисел на карточках, т.е. n = 2. Благоприятствующих исходов 4, m = 4.
Итак, P(A)=4/16=0,25.
III тип
Пример 7. Конференция длится три дня. В первый и второй день выступают по 20 докладчиков, в третий день – 10. Какова вероятность того, что доклад профессора Сидорова выпадет на третий день, если порядок докладов определяется жеребьевкой?
Решение. Испытание – присвоение докладу профессора какого-то одного из всех возможных порядковых номеров от 1 до 50 для выступления (в жеребьевке участвует 20+20+10=50 человек, таким образом, доклад профессора Сидорова может получить один из 50 номеров). Таким образом, элементарных исходов всего 50, n=50. Событие А – «присвоение докладу одного из 10 последних номеров». Благоприятствующими исходами будут последние 10 номеров. По формуле вероятность P(A)=10/50=1/5=2/10=0,2.
Жеребьевка в задачах по теории вероятностей представляет собой установление случайного соответствия между людьми и упорядоченным набором чисел. В данном примере установление соответствия рассматривалось с точки зрения того, какое число могло быть присвоено конкретному человеку. Можно к установлению соответствия подойти с другой стороны, а именно: установить, кто из людей мог бы занять конкретное место.
Пример 8. На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 6 прыгунов из Голландии и 2 прыгуна из Аргентины. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что четырнадцатым будет выступать прыгун из Аргентины.
Решение. Испытание – выбор человека на четырнадцатое место. Cобытие А – «на четырнадцатое место попал аргентинец». Количество элементарных исходов равно количеству людей, которые могли бы по жеребьевке попасть на данное место, n = 40. Количество благоприятствующих исходов равно числу аргентинцев, т.е. m =2. Искомая вероятность P(A)= 2/40=0,05.
Пример 9. В классе 26 учащихся, среди них два друга – Андрей и Сергей. Учащихся случайным образом делят на 2 равные группы. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
Решение. Испытание состоит в разделении группы из 26 учащихся на две подгруппы. Обозначим событие А – «Андрей и Сергей попали в одну группу». Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 12 человек из 25 оставшихся одноклассников. Таким образом всего элементарных исходов m = 25, благоприятствующих исходов n = 12. Вероятность того, что второй окажется среди этих 12 человек, равна P(A)=12/25 = 0,48.
Пример 10. За круглый стол на 201 стульев в случайном порядке рассаживаются 199 мальчиков и 2 девочки. Найдите вероятность того, что между двумя девочками будет сидеть один мальчик.
Решение. Испытание состоит в рассаживании 201 ребенка за круглый стол. Обозначим событие А – «Между девочками сидит один мальчик». Пусть первой за стол сядет девочка, тогда есть два места через одно от нее, на каждое из которых претендует 200 человек, из которых только одна девочка. Таким образом всего исходов m = 200, благоприятствующих исходов n = 2. Вероятность того, что между двумя девочками будет сидеть один мальчик, равна P(A)=2/200 или P(A) =0,01.
Пример 11. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 спортсменов из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России.
Решение. Испытание состоит в выборе спортсмена в пару с Орловым. Обозначим событие А – «Руслан Орлов играет с бадминтонистом из России». В первом туре Руслан Орлов может сыграть с 25 бадминтонистами, поэтому n = 25. Благоприятствующих исходов m= 9 (cтолько в паре с Орловым спортсменов из России). Значит, вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна P(A)=9/25=0,36.
Пример 12. В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?
Решение. Испытание состоит в выборе двух человек для похода в магазин. Обозначим событие А – «Турист Д пошёл в магазин». Всего туристов пять, случайным образом из них выбирают двоих. Вероятность быть выбранным равна P(A)=2/5 = 0,4.
Пример 13. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
Решение. Испытание состоит в определении начала игры команды «Физик». Событие А – «Команда «Физик» начинает игру ровно два раза». Обозначим «1» ту сторону монеты, которая отвечает за начало игры команды «Физик», другую сторону монеты обозначим «0». Выпишем все элементарные исходы: 000, 001, 010, 011, 100, 101, 110, 111; n=8. Тогда благоприятствующими событию А являются такие: 110, 101, 011; m=3. Тем самым, искомая вероятность P(A)=3/8=0,375.
Пример 14. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
Решение. Испытание состоит в определении порядка выступления трех команд. Событие А – «Группа из Дании выступает после группы из Швеции и после группы из Норвегии». Есть 6 способов взаимного расположения среди выступающих: ДШН, ДНШ, ШДН, ШНД, НДШ, НШД (Д – Дания, Ш – Швеция, Н – Норвегия), поэтому n=6. Благоприятствующими событию А являются следующие исходы: ШНД и НШД, поэтому m=2. Вероятность того, что группы случайным образом будут распределены именно так, равна P(A) = 2/6 = 0,33.
Проведенный нами анализ задач материалов ЕГЭ по теории вероятностей (В10) привел к выводу о том, что классическое определение вероятности можно применить для решения примерно трети заданий Открытого банка ЕГЭ. При решении задачи важно правильно и четко определить в каждой ситуации, о каком испытании идет речь, выявить в соответствии с классическим определением вероятности количество равновозможных элементарных исходов, определить число благоприятствующих испытанию исходов.

