Принцип инерции Ньютона в его собственной формулировке говорит, что любое тело продолжает находиться в состоянии покоя или прямолинейного и равномерного движения до тех пор, пока оно не будет вынуждено изменить это состояние под действием приложенных сил.
Позднее этот принцип, названный первым законом Ньютона, был уточнен – оказалось, что принцип инерции выполняется не во всех системах отсчета и сегодня формулировка первого закона Ньютона такова: существуют системы отсчета, в которых тело при отсутствии внешнего воздействия или в случае, когда внешние воздействия компенсируются, сохраняет состояние покоя или прямолинейного равномерного движения.
Такие системы отсчета, в которых выполняется первый закон Ньютона, называются инерциальными системами отсчета (ИСО). В формулировке первого закона Ньютона корректнее пользоваться термином «внешнее воздействие», чем термином «действие других тел», так как первый термин позволяет использовать закон как в случае непосредственного воздействия со стороны других тел, так и в случае, когда тело может находиться в каком-то внешнем поле (гравитационном, электрическом, магнитном и т.д.).
Обычно говорят, что неинерциальными системами отсчета (НИСО) являются системы отсчета, в которых первый закон Ньютона не выполняется. И это правильно.
В школьных учебниках по физике в качестве НИСО приводят общеизвестные примеры, например, автобус при резком торможении (или резком рывке вперед), когда на стоящего в автобусе человека толкает вперед (или назад) непонятно откуда взявшаяся сила, или тележку с капельницей на штативе и мензуркой под нею, установленных на тележке, в случаях ускоренного или замедленного движений тележки [1-3]. Эта сила (сила, появляющаяся в НИСО) называется силой инерции.
Обратим внимание – в этих примерах НИСО (автобус, тележка) движутся ускоренно или замедленно, но поступательно. Но силы инерции появляются и во вращающихся системах отсчета. Например, сила, появляющаяся во вращающихся каруселях и направленная от центра карусели. Таким образом любая система отсчета, движущаяся относительно ИСО с ускорением или любая вращающаяся система отсчета является неинерциальной системой отсчета (НИСО).
В школе обычно довольствуются первой частью этого определения НИСО, хотя и доводят до школьников, что Земля (а она вращается вокруг собственной оси и вращается по определенной орбите вокруг Солнца) и любая система отсчета, связанная с Землей, с достаточной точностью могут считаться ИСО. Эту «достаточную точность» школьникам можно показать и нужно показать.
При преподавании общей физики в высших учебных заведениях строгий вывод формул, определяющих силы инерции, делается и основной итог из них прост: Сила инерции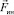 
появляется только в НИСО, она всегда направлена против ускорения 
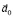НИСО и равна произведению массы m наблюдаемого тела на ускорение 
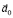НИСО, взятое с противоположным знаком [4]:
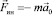. (1)
Эта формула справедлива для любого типа НИСО – как для НИСО, движущейся поступательно с ускорением, так и для вращающейся НИСО. Только если для первого типа НИСО вопросов с ускорением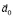 
нет, то ясно, что для второго типа НИСО ускорение 
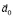должно быть выражено через угловую скорость 
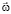вращения НИСО.
Вернемся к Земле. Почему её можно считать ИСО? Для ответа на этот вопрос надо сравнить возникающие на поверхности Земли силы инерции, действующие на тело с массой m, с легко определяемой реальной силой, действующей на это тело, например, с силой тяготения (берем модули сил):
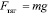. (2)
Во вращающейся НИСО возникают силы инерции двух видов – это центробежная сила
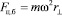(3)
и Кориолисова сила (сила Кориолиса)
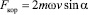. (4)
Здесь, если Землю выбрать в качестве системы отсчета, ω – угловая скорость вращения Земли вокруг собственной оси,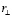 
– расстояние от наблюдаемого тела m до оси вращения Земли, v – скорость тела m относительно Земли, α – угол между векторами угловой скорости 
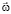Земли и скорости 
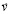тела, т.е.,
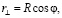
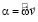, (5)
где R – радиус Земли, φ – широта места, где находится тело m. Чтобы оценить относительные величины этих трех видов сил можно взять максимальные значения сил инерций (нас интересуют именно они):
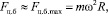
(6)
Тогда, подставив известные значения ω и R, получим
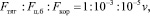(7)
т.е., видно, что силами инерции можно пренебречь с «достаточной точностью» и действительно Земля и любой объект, связанный с Землей, представляют собой неплохие ИСО. Аналогично можно убедиться и в том, что силами инерции, возникающими за счет вращения Земли вокруг Солнца, также можно пренебречь.
Хотелось бы обратить внимание еще на один момент, который не мешало бы знать школьникам. Это совершенно одинаковый вид сил тяготения и инерции:
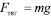
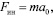(8)
где g – ускорение свободного падения,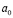 
– ускорение НИСО. Видно, что сила инерции, появляющаяся в НИСО, вызывает одинаковое ускорение тел, независимо от массы и это приводит к сходству этой силы с силой тяготения, которая тоже сообщает телу одно и то же ускорение g (ускорение свободного падения), независимо от массы. Это наталкивает на мысль об их эквивалентности, что было выражено в постулате А. Эйнштейна о том, что сила инерции и сила тяготения эквивалентны. Этот постулат, называемый еще постулатом Эйнштейна об эквивалентности был одним из постулатов, послуживших основой общей теории относительности (ОТО).
Вернемся к определению НИСО – это системы отсчета, в которых первый закон Ньютона не выполняется. В таких системах отсчета даже при отсутствии реальных сил, действующих на тело, как бы в противоречии с первым законом Ньютона тело начинает двигаться с ускорением (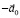
), равным по величине, но противоположным по направлению ускорению 
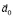данной системы отсчета, относительно которой ведется наблюдение за движением тела, т.е., действительно как-бы нарушается первый закон Ньютона. Но всё это из-за того, что сила инерции 
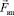не относится к реальной силе, возникающей из-за взаимодействия тела с другими телами или полями. Проведем мысленный опыт. Допустим, что тело массой m находится в закрытой, удаленной от всех внешних тел кабине К, движущейся в каком-то направлении с ускорением 
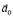(см. рисунок), т.е., кабина представляет НИСО. Пусть на пути возможного перемещения тела имеется преграда П. На тело действуют две силы – сила инерции 
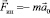и сила реакции опоры (преграды) 
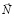, которые равны по величине, но противоположны по направлению (вспомните третий закон Ньютона), т.е., их векторная сумма равна нулю:
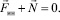(9)
Тело будет покоится, т.е., первый закон Ньютона выполняется и в НИСО, если силу инерции ставить наравне с реальными силами. Это не означает, что следует отказаться от общепринятого определения НИСО, но не мешает всегда держать в уме то, о чем было сказано выше. Тем более, что в ОТО (общая теория относительности) все системы отсчета эквивалентны и не стоит забывать принцип эквивалентности сил инерции и тяготения.
Заключение
В статье постарались обратить внимание преподавателей физики (в школах, вузах) на некоторые моменты в первом законе Ньютона, на которые в школьных учебниках по физике (и не только в школьных) не уделяется достаточного внимания, хотя преподаватели (учителя) должны все это «держать в уме» в процессе преподавания физики или даже постараться объяснить (в школах с углубленным изучением физики).