Scientific journal

International Journal of Experimental Education

ISSN 2618–7159

ИФ РИНЦ = 0,425

Богатейший ресурс математики, которая концентрирует знания, необходимые в повседневной жизни – для решения практических задач, для ориентации и коммуникации в обществе и в окружающем пространстве в целом, играет важную роль как в интеллектуальном развитии личности, так и ее профессиональном становлении.

Одна из целей школьной математики – подготовить учащихся к изучению реальных ситуаций с помощью математических моделей – в значительной степени не достигается на уровне требований международной программы по оценке функциональной грамотности учащихся в области математики PISA (Programme for International Student Assessment).

Российские школьники принимали участие в шести циклах мониторинга PISA: в 2000 – 2015 годах (табл. 1).

Результаты оценки математической грамотности, например, в 2012 году показывают, что 71– российских школьников достигли лишь порогового уровня (2-го уровня из 6 по международной шкале). Анализ результатов по видам математической деятельности, показывает, что российские школьники по умениям формулировать, применять, а особенно по умениям интерпретировать значительно отстают от школьников других стран.

Таблица 1

Результаты оценки математической грамотности 15-летних учащихся России (PISA)

Математическая грамотность (в проведенном исследовании) – способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину [2]. Содержание этого понятия уточняется так. Под математической грамотностью понимается способность учащихся выполнять следующие действия: распознавать проблемы, возникающие в окружающей действительности, которые могут быть решены средствами математики; формулировать эти проблемы на языке математики; решать эти проблемы, используя математические знания и методы; анализировать использованные методы решения; интерпретировать полученные результаты с учетом поставленной проблемы; формулировать и записывать окончательные результаты решения поставленной проблемы.

Перечисленные действия перекликаются с компонентами метода математического моделирования. Одной из причин низкого уровня использования метода математического моделирования к решению жизненных задач (задач с практическим содержанием) является отсутствие реализации этой цели в действующих учебниках основной и средней школы [2].

Нами был проведен анализ семнадцати действующих школьных учебников (задачников) по алгебре 7-11 классов, результаты которого отражены в табл. 2. В средних столбцах таблицы указано количество исследуемых задач с практическим содержанием по типам, в последнем столбце – общее количество текстовых задач в учебнике (задачнике).

Для удобства приняты обозначения:

Л – задачи, сводящиеся к исследованию линейных функций.

К– задачи, сводящиеся к исследованию квадратичных функций.

Д – задачи, сводящиеся к исследованию дробно-рациональных функций.

Р – задачи, сводящиеся к исследованию рациональных функций высших степеней.

Т – задачи, сводящиеся к исследованию тригонометрических функций.

ЛГ – задачи, сводящиеся к исследованию логарифмических функций.

П – задачи, сводящиеся к исследованию показательных функций.

И – задачи, сводящиеся к исследованию иррациональных функций.

Таблица 2

Количество задач с практическим содержанием в школьных учебниках

Анализ показал, что в современных учебниках алгебры среди довольно большого количества текстовых задач ничтожно мало задач с практическим содержанием, кроме того, нет вовсе задач с практическим содержанием, сводящихся к решению логарифмических, показательных, тригонометрических уравнений и неравенств. Это противоречие говорит о необходимости разработки методики обучения учащихся решению задач с практическим содержанием в рамках школьного курса алгебры.

В отличие от исследований Е.С. Янушпольской, Ц.Д. Дашинимаевой, Е.Н. Эрентраут, в которых рассматриваются вопросы обучения учащихся решению прикладных, практических и практико-ориентированных задач в системе общего образования и в профильной школе, мы считаем важным разработать технологию обучения учащихся решению задач с практическим содержанием в рамках реализации функциональной линии школьного курса математики с целью обучения методу математического моделирования.

Мы считаем, что если: усилить практический аспект подготовки школьников за счет использования теории практико – ориентированного обучения (Г.К. Селевко); определить источниковую базу задач с практическим содержанием; включить эти задачи в функциональный контекст с 7 класса; уточнить компоненты метода математического моделирования для решения задач выбранного класса; организовать обучение отдельным компонентам метода математического моделирования с использованием совокупности специально подобранных математических задач; уровень сформированности у учащихся умений решать задачи с практическим содержанием выбрать алгоритмический (согласно В.П. Беспалько); целью средней перспективы определить подготовку к итоговому контролю (ОГЭ, ЕГЭ), то уровень сформированности умений использования приобретенных знаний и умений в практической деятельности и повседневной жизни повысится.

В контрольно-измерительных материалах ЕГЭ содержится четыре задания, для выполнения которых требуется уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни. Наибольшую трудность для школьников представляет задача B11 (2015-2016 г.), анализ результатов ее выполнения показывает, что средний процент выполнения, например, в 2015 году составляет 44,2 [6].

В 2015-2016 годах в открытом банке заданий ЕГЭ по математике содержится 1907 задач типа В11, относящихся к 66 прототипам (в 2012-2014 годах – 2110 задач, 67 прототипов) [3]. Приняв за основу использование этих задач в школьном обучении, включив их в функциональный контекст, мы разделили задачи следующим образом: сводящиеся к исследованию линейных функций (4 прототипа, включать с 7 класса); сводящиеся к исследованию целых рациональных функций (14 прототипов, включать с 8 класса), дробно-рациональных функций (15 прототипов, включать с 9 класса); сводящиеся к исследованию иррациональных функций (10 прототипов, включать с 9 класса); сводящиеся к исследованию трансцендентных функций – показательных (3 прототипа, включать с 10 класса), логарифмических (4 прототипа, включать в 11 классе), тригонометрических (16 прототипов, включать с 10 класса) [4].

Задачи с практическим содержанием типа В11 имеют рад особенностей, их условие описывает физические или экономические процессы. Например.

Задача 1. Некоторая компания продает свою продукцию по цене 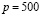руб. за единицу, переменные затраты на производство одной единицы продукции составляют 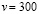руб., постоянные расходы предприятия f=700000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле

.

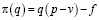Определите месячный объём производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет равна 300000 руб.

Задача 2. Находящийся в воде водолазный колокол, содержащий 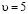молей воздуха при давлении 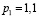атмосферы, медленно опускают на дно водоема. При этом происходит изотермическое сжатие воздуха. Работа, совершаемая водой при сжатии воздуха, определяется выражением

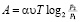(Дж),

где 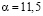– постоянная, а 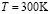– температура воздуха, 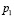(атм) – начальное давление, а 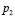(атм) – конечное давление воздуха в колоколе. До какого наибольшего давления 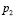можно сжать воздух в колоколе, если при сжатии воздуха cовершаетcя работа не более чем 34500 Дж? Ответ приведите в атмосферах.

Задача 3. Скорость колеблющегося на пружине груза меняется по закону

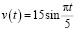(см/с),

где t – время в секундах. Какую долю времени из первых двух секунд скорость движения превышала 7,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.

Решение задач выбранного класса группируется вокруг таких видов математической деятельности, как структурирование ситуации таким образом, чтобы ее можно было моделировать; перевод реальной ситуации в математическую структуру; интерпретация математической модели с учетом реальной ситуации; работа с математической моделью; оценка правильности модели; рассуждения, анализ, критика модели и полученных результатов; запись, характеризующую модель и полученные результаты (включая ограничения полученных результатов); контроль процесса моделирования.

Представления о структуре математического моделирования, его компонентах, специфике отдельных его этапов создают базу для развития общих навыков применения математики к решению практических задач, обеспечивают практическую направленность преподавания математики (Л.Д. Кудрявцев, Б.В. Гнеденко, Г. Фройденталь). Изучив подходы А.Я. Блоха, С.И. Шварцбурда, В.В. Фирсова, Н.Я. Виленкина, В.А. Стукалова, А.Н. Тихонова и других ученых к понятию «метод математического моделирования» [1], заключаем, что решение задач типа В11 невозможно без применения внешне-математического моделирования. На основе анализа этапов математического моделирования, выделенных В. В. Фирсовым, мы адаптировали и уточнили содержание основных компонентов метода следующим образом. Компоненты метода математического моделирования: формализация (проанализировать условие задачи, подставить все известные значения величин в заданную формулу, выявить условие для составления уравнения или неравенства, составить уравнение или неравенство); решение задачи внутри построенной математической модели (определить тип полученного уравнения или неравенства и решить его, осуществить отбор полученных решений с учетом заданных ограничений); интерпретация (перевести полученные решения на язык предметной области, заданной по условию задачи, получить искомую информацию об исследуемом объекте, процессе, явлении и записать ответ на поставленный вопрос).

Рассмотрим решение задачи 3 с использованием указанного алгоритма.

1) Составим неравенство

;

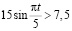2) Преобразуем:

;

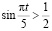3) Решим:

;

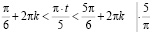4) Получим:

.

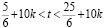5) При :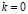

.

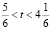По условию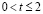

Составим систему и решим ее

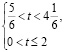
Доля времени из первых двух секунд, когда скорость превышала 7,6 см/с, составляет:

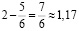с.

Ответ: 1,17.

Реализация компонентов метода математического моделирования в решении рассматриваемых задач осложняется особенностями этих задач. Например, в решении задачи 3 на этапе интерпретации требуется произвести отбор корней тригонометрического неравенства, руководствуясь тремя позициями: физическая суть рассматриваемого процесса ограничивает значение аргумента тригонометрической функции; требование задачи – определить долю времени из первых двух секунд и требование округлить полученный результат. Поэтому, обучение методу математического моделирования в целом предполагает отработку его отдельных компонентов. В частности, для успешной реализации этапа внутримодельного решения задач типа В11, сводящихся к решению тригонометрических неравенств, нами проанализированы прототипы задач открытого банка ЕГЭ, выявлены типы моделей (тригонометрических неравенств), объединены в дидактически целесообразные совокупности и организовано обучение их решению разными способами. Для успешной реализации этапа интерпретации при решении задач типа В11, сводящихся к решению тригонометрических неравенств, нами разработана целая система обучения учащихся проведению отбора корней [5]. Определено содержание понятия отбора корней тригонометрического уравнения и неравенства, выявлены и систематизированы виды и способы проведения отбора, найдены эффективные интерактивные средства обучения учащихся проведению отбора корней, а также разработаны и другие компоненты методической системы обучения.

На заключительном этапе обучения методу математического моделирования важно организовать применение метода в целом и в комбинации с другими методами.

Систематическое решение задач рассматриваемого типа в рамках функциональной линии школьного курса математики, начиная с 7 класса, позволяет организовать деятельность, включающую критическое мышление, анализ, размышления, обобщение и интерпретацию информации, полученной в результате исследования. Такая деятельность является сердцевиной высокого уровня математической грамотности.