В настоящее время наблюдается рост использования достижений фундаментальных наук в медицине. Медицинские объекты исследования иногда представляют собой сложную динамическую систему. Например, меняется со временем состояние пациентов, эпидемиологические показатели регионов, здоровье населения и множество других факторов. При исследовании таких систем в медицине используют различные подходы, в том числе и математические методы [1-3].
В данной работе предлагается использовать математический метод проекции градиентов [4,5] для выявления влияния степени выраженности симптомов на результат диагностирования, что соответствует изменению состояния пациента наблюдаемое в определенный промежуток времени. Для упрощения возьмем, что симптомокомплекс не меняется, а меняется степень выраженности того или иного симптома. Случай, когда меняется и симптомокомплекс и степень выраженности симптомов относится к весьма сложным системам.
Рассмотрим несколько случаев с различной степенью выраженности симптома пациента, при данном симптомокомплексе. Диагнозы ставим на основе разработанной математической модели диагностирования с применением метода проекции градиентов. Итак, у пациента наблюдается плохой сон, одышка, учащенное сердцебиение, боль в области сердца, потливость, потеря в весе. Пусть состояние пациента задано множеством:
X={0.4/X4, 0.2/X5, 0.5/X6, 0.2/X7, 0.6/X8, 0.1/X9}.
Значения (0.4; 0.2; 0.5; 0.2; 0.6; 0.1;) означают степень выраженности симптомов для данного пациента, которую представим в виде вектора 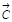 :
:
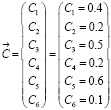 .
.
Введем понятие полезности для данного нозологического класса, взятые из известной диагностической таблицы, в виде матрицы А:

Таким образом, имеем: 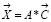
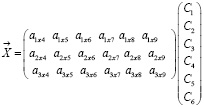
Рассмотрим, как будут меняться результаты диагностики с изменением степени выраженности симптома: потеря веса (0.1, 0.3, 0.5, 0.7, 0.9).
0.4/X4, 0.2/X5, 0.5/X6, 0.2/X7, 0.6/X8, 0.1/X9
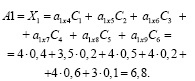
Аналогично:
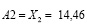 и
и 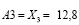 .
.
Отсюда множество: μ (Aio)~Ao
(μ(A1o))=max (6,8; 14.46; 12.8;).
Поскольку: A(*)=μ~ (A2o)=14.46 то, оптимальной альтернативой является заболевание A2. Отсюда диагноз: наблюдается заболевание диффузный токсический зоб для заданного состояния системы и наблюдаемого у пациента симптомокомплекса.
0.4/X4, 0.2/X5, 0.5/X6, 0.2/X7, 0.6/X8, 0.3/X9
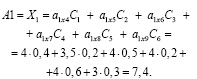
Аналогично:
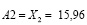 и
и 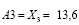
Отсюда множество:
μ(Aio)~Ao (μ(A1o))=max (7.4; 15.96; 13.6).
Итак A(*)=μ~ (A2o)=15.96, следовательно оптимальной альтернативой является заболевание A2. Диагноз: наблюдается заболевание диффузный токсический зоб для заданного состояния системы и наблюдаемого у пациента симптомокомплекса.
0.4/X4, 0.2/X5, 0.5/X6, 0.2/X7, 0.6/X8, 0.5/X9
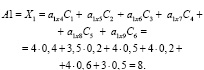
Аналогично:
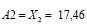 и
и 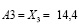
Отсюда множество:
μ(Aio)~Ao (μ(A1o))=max (8; 17.46; 14.4;).
Поскольку A(*)=m~ (A2o)=17.46 то, оптимальной альтернативой является заболевание A2. Ставится диагноз: заболевание диффузный токсический зоб для заданного состояния системы.
0.4/X4, 0.2/X5, 0.5/X6, 0.2/X7, 0.6/X8, 0.7/X9
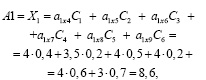
Аналогично:
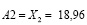 и
и 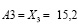 .
.
Итак, множество:
μ(Aio)~Ao (μ(A1o))=max (8.6; 18.96; 15.2).
Следовательно, поскольку:
A(*)=μ~ (A2o)=18.96,
то оптимальной альтернативой является заболевание A2. Ставится диагноз: наблюдается заболевание диффузный токсический зоб для заданного состояния системы и симптомокомплекса.
0.4/X4, 0.2/X5, 0.5/X6, 0.2/X7, 0.6/X8, 0.9/X9
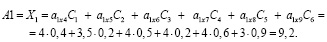
Аналогично:
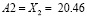 и
и 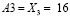 .
.
Получаем множество:
μ(Aio)~Ao (μ(A1o))=max (9.2; 20.46; 16).
Отсюда
A(*)=μ~ (A2o)=20.46,
значит, оптимальной альтернативой является заболевание A2. Следовательно, для заданного состояния системы и симптомокомплекса наблюдается заболевание диффузный токсический зоб. Результаты внесены в таблицу.
Результаты диагностики для различной степени выраженности симптома
|
№ |
Состояния |
контрольная группа (А1) |
диффузный токсический зоб (А2) |
вегетативная сосудистая дистония (А3) |
|
1 |
0.4/X4, 0.2/X5, 0.5/X6, 0.2/X7, 0.6/X8, 0.1/X9 |
6.8 |
14.46 |
12.8 |
|
2 |
0.4/X4, 0.2/X5, 0.5/X6, 0.2/X7, 0.6/X8, 0.3/X9 |
7.4 |
15.96 |
13.6 |
|
3 |
0.4/X4, 0.2/X5, 0.5/X6, 0.2/X7, 0.6/X8, 0.5/X9 |
8 |
17.46 |
14.4 |
|
4 |
0.4/X4, 0.2/X5, 0.5/X6, 0.2/X7, 0.6/X8, 0.7/X9 |
8.6 |
18.96 |
15.2 |
|
5 |
0.4/X4, 0.2/X5, 0.5/X6, 0.2/X7, 0.6/X8, 0.9/X9 |
9.2 |
20.46 |
16 |
В целом, диагноз не изменился, однако с увеличением степени выраженности симптома (потеря веса), вероятность заболевания токсический зоб значительно увеличивается по сравнению с заболеванием диффузный токсический зоб. Отсюда можно сделать вывод: симптом в большей степени относится к заболеванию токсический зоб.
Влияние изменения состояния системы (степени выраженности симптомов) на результат диагностики, как показано в данной работе, очевиден. Следует отметить, что известный байевский метод диагностирования не позволяет сделать аналогичный вывод.
Изменения состояния пациента можно рассматривать как динамический ряд и в дальнейшем, следует его усовершенствовать. Не исключается возможность использования данного метода для прогнозирования течения заболевания, что является актуальной проблемой, поскольку медицина постоянно сталкивается с влиянием внешних и внутренних факторов (действие радиации, лекарственных препаратов, ухудшения или улучшение здоровья пациента и др.). В таких условиях меняется степень выраженности симптома. Модель диагностирования методом проекции градиентов можно использовать, в целях обучения, в медицинских вузах. Применение новых методов диагностирования, каковым является представленная математическая модель, основывающаяся на применении базы данных, взятых из практического здравоохранения, дает возможность повысить объективность при принятии решений. При соответствующей технической реализации, с помощью электронно-вычислительной техники, может быть использована модель для мониторинга в медицине.

