Конвективные движения, возникающие при изотермической взаимной диффузии, когда на величину плотности влияет только одна постоянная термодинамическая сила ∇c описываются аналогично обычной тепловой конвекции, при этом диффузия выполняет роль теплопроводности. Если существенны градиенты более чем одного диффундирующего свойства, т.е. наличие двух сил ∇c и ∇T, то могут возникнуть качественно новые эффекты. Например, во многих рассматриваемых экспериментально системах неустойчивость может формироваться даже тогда, когда внизу смесь более плотная, т.е. при отрицательном направлении плотности. При этом присутствие перекрестных эффектов может осложнить явления, возникающие при изотермической взаимной диффузии. В этом случае возникновение термо-концентрационной конвекции обусловлено неоднородностью, как температуры, так и концентрации. Явление, приводящее к потере устойчивости в таких системах, получило название «двойной диффузии». Изотермическая диффузия в тройных смесях также характеризуется наличием двух независимых градиентов концентрации.
Существующие экспериментальные данные, как по исследованию смешения, как в бинарных, так и в трехкомпонентных газовых смесях, показали, что конвективные потоки, возникающие при определенных условиях, налагаясь на молекулярный перенос, приводят к потере устойчивости механического равновесия системы, т.е. к диффузионной неустойчивости. Сравнительный анализ, приводимых в литературе данных, по физическому смыслу взаимосвязан с проблемами потери устойчивости механического равновесия в случае тепловой конвекции.
Изучение наиболее общих особенностей в определении границы перехода из одного режима в другой возможно на основе методов линейной теории устойчивости. Однако возможности указанных методов ограничены. При изучении нестационарных процессов эти методы не позволяют точно определить критические условия перехода «диффузия – конвекция». Также затруднительно на основе теории устойчивости описать динамику конвективных течений. Такие вопросы могут быть решены с помощью методов математического моделирования, которые должны соответствовать конкретной задаче многокомпонентного смешения.
Таким образом, на данный момент актуальным остается вопрос об определении границы устойчивости для бинарных и многокомпонентных газовых смесей с учетом нестационарных условий.
Задачи исследования. Разработать математическую модель для моделирования сложного массопереноса в бинарных и трехкомпонентных газовых смесях при различных давлениях и температурах.
Объектом исследования является процесс неизотермического смешения бинарных газовых смесей и изотермического смешения трехкомпонентных газовых смесей.
Предметом исследования является неустойчивость механического равновесия в неизотермических бинарных и изотермических трехкомпонентных газовых смесях.
Методы исследования. Используются аналитические методы исследования многокомпонентного массопереноса, основанные на решении системы уравнений Навье-Стокса, диффузии и состояния среды в приближении малых возмущений, a также схема расщепления по физическим параметрам с использованием схемы продольно-поперечной прогонки.
Диффузионная неустойчивость
Наиболее интенсивно изучаемой в последнее время особенностью диффузионного смешения является диффузионная неустойчивость в условиях устойчивой стратификации плотности. Эту особенность называют также аномальной гравитационной конвекцией. Проводя исследования по изучению диффузионного термоэффекта в трехкомпонентных газовых смесях в трубке Лошмидта Миллер и Мейсон обнаружили, что изменение температуры по обе стороны от границы раздела газов для некоторых систем в течение нескольких десятков секунд имело колебательный характер, хотя предполагалось ее монотонное нарастание. Также были замечены нерегулярные колебания концентраций компонентов при диффузии тройных смесей [1]. В этой публикации было отмечено, что длительность колебательного режима при давлениях, близких к атмосферному, и комнатной температуре не превышает нескольких десятков секунд. Таким образом, представленные в [1] исследования, подтвердили экспериментальные результаты, описанные в [2–3]. Дальнейшие исследования диффузионной неустойчивости позволили измерять парциальные расходы компонентов через диффузионный капилляр и наблюдать осцилляции концентраций в течение длительного времени [4–5].
При анализе экспериментальных исследований по диффузии, было показано, что возникновение диффузионной неустойчивости в трехкомпонентных газовых смесях связано с выполнением ряда необходимых условий [6–7]:
1) бинарная смесь газов (1 + 2) расположена вверху, чистый газ (3) – внизу, ρ2 > ρ3 > ρ1; ρ(1+2) < ρ3; D13 > D23;
2) бинарная смесь газов (1 + 2) расположена внизу, чистый газ (3) – вверху, ρ2 > ρ3 > ρ1; ρ(1+2) > ρ3; D13 > D23;
3) бинарная смесь газов (1 + 2) расположена вверху, бинарная смесь (3 + 2) – внизу, ρ2 > ρ3 > ρ1; ρ(3+2) > ρ(1+2); D12 > D32;
4) бинарная смесь газов (1 + 2) и чистый газ (3) могут быть расположены либо вверху, либо внизу, ρ2 > ρ3 > ρ1; ρ(1+2) = ρ3; D13 > D23, в этом варианте неустойчивый процесс возможен при любой ориентации смесей, но только для разных параметров, в частности, давления.
Необходимые условия для возникновения конвекции при диффузионном смешении должны быть дополнены достаточными условиями:
1. Смесь газов должна состоять из компонентов, коэффициенты диффузии которых в чистый газ, отличаются в несколько раз (например, DHe-Ar больше 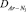 примерно в три раза).
примерно в три раза).
2. Неустойчивость возникает в определенных интервалах концентраций компонентов.
3. Влияние давления существенно.
4. Диаметр диффузионного канала должен быть не менее определенного размера. Играет роль даже длина диффузионного канала, и под каким углом к вертикали он расположен.
5. На возникновение неустойчивости оказывает влияние температура.
6. В некоторых трехкомпонентных смесях газов неустойчивость появляется независимо от исходной ориентации компонентов в диффузионном аппарате.
7. С уменьшением вязкости диффундирующей смеси возникновение неустойчивого (нестабильного) процесса более вероятно.
Результаты, перечисленных выше экспериментальных исследований по изучению диффузионной неустойчивости проводились с газовыми системами, в которых парциальные плотности и КВД компонентов существенно отличались.
Явление диффузионной неустойчивости, в природе приводит к удивительным процессам и явлениям. Возникновение мощных конвективных потоков в атмосфере, когда наблюдается отчетливая граница между теплыми и холодными воздушными слоями различной влажности. При нагреве, за счет солнечного облучения льда образуются не вертикальные каналы, заполненные однородной жидкой средой, a наклонные, заполненные жидкостью различной плотности. В океане также наблюдаются слои с резко выраженными границами солености и температуры, что приводит к сложному конвективному движению внутри жидкости. При вулканической активности на морском дне из вытекающей лавы образуются твердые осаждения, неоднородные по высоте, что можно объяснить влиянием двух термодинамических сил, вызванных различием температур вытекающей из жерла вулкана и окружающей жидкости, их неоднородности по плотности. В небесных телах можно отметить перераспределение потенциальной энергии между вращательным и поступательным движением жидкости или газа. При наличии подогрева снизу, вызванного термоядерными процессами в звездах можно наблюдать конвективный перенос гелия и водорода в короне солнца.
Экспериментальное изучение двойной диффузии проводилось в основном на жидких растворах. В соответствующих опытах и при их теоретическом анализе было показано, что особенности диффузионной неустойчивости при двойной диффузии обусловлены наличием двух термодинамических сил и их независимым вкладом в поле плотности массы. На основе общей линейной теории конвективной устойчивости жидкости получены критические числа Рэлея, характерные критическим движениям. Теоретическое описание наблюдаемого явления получило экспериментальное подтверждение для магнито – и электрически проводящих жидкостей, что нашло широкое применение в промышленности.
Численное моделирование концентрационной задачи смешения трехкомпонентной газовой смеси
Рассмотрим численное моделирование влияния давления на возникновения механического равновесия в трехкомпонентной смеси 0,5312Ar + 0,4688He – N2 на основе решения системы уравнений (1), состоящей из уравнения Навье-Стокса, уравнения неразрывности, уравнении для концентрации в цилиндрическом канале размерами L1 и L2 при различных значениях давления. Основными параметрами регулирования в трехкомпонентной смеси является давление. Исследуется процесс, когда тяжелый газ Ar и легкий газ He, находиться в верхней части указанного канала, a средний N2 – в нижней.
Экспериментальные результаты, приведенные на рис. 1 в виде зависимости безразмерного параметра α от давления, свидетельствуют о том что, при p* = 1,5 МПа наблюдается существенное расхождение между экспериментальными и вычисленными в предположении диффузии концентрациями компонентов [8]. Безразмерный критерий α для компонента i определяется отношением измеренной концентрации к ее теоретическому значению для устойчивой диффузии, вычисленной по уравнениям Стефана – Максвелла.
Рис. 1. Зависимость параметра α от давления:  – точки – экспериментальные результаты;
– точки – экспериментальные результаты;  – вычисленные результаты
– вычисленные результаты
Согласно системе уравнений (1) зададим начальное и граничное условия.
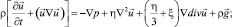
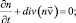
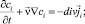
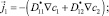
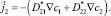 (1)
(1)
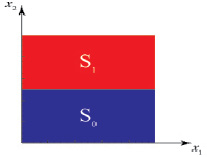
Рис. 2. Начальные условия для трехкомпонентного смеся 0,5312Ar + 0,4688He – N2
Начальные условия: для компонентов скорости –
ui(x1, x2, 0) = 0, (2)
для кoнцeнтpaции:
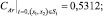 (3)
(3)
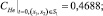 (4)
(4)
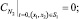 (5)
(5)
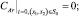 (6)
(6)
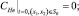 (7)
(7)
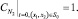 (8)
(8)
Начальные условия для рассматриваемой системы приведены на рис. 2.
Для решения задачи движения газа в цилиндрической области воспользуемся схема расщепления по физическим параметрам [8–9]. На первом этапе перенос количества движения осуществляется только за счет конвекции и диффузии. Промежуточное поле скорости находится методом дробных шагов, при использовании метода прогонки.
Профили концентрации трехкомпонентной газовой смеси при различных давлениях и времени смешения
Расчёты проводились на равномерной прямоугольной сетке размером 64×64. Давление выбиралось в диапазоне p ≈ 0,2...3,0 МПа при Т = 298,0 К. Шаг по времени принимался равным 0,005 секунд. В расчетах нестабильность механического равновесия была зарегистрирована при р = 1,7 МПа.
На рис. 3 изображена динамика изменения концентрации компонентов в последовательные моменты времени при р = 1,5 МПа. На всех рисунках профиль концентрации компонентов плоский, что свидетельствует о диффузионном процессе.
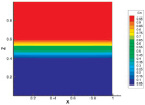
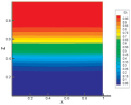
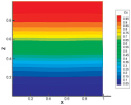
а б c
Рис. 3. Динамика изменения концентрации по времени для системы 0,5312Ar + 0,4688He – N2 при р = 1,5 МПа: а – t = 0,25; б – t = 1; c – t = 2
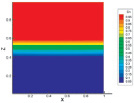
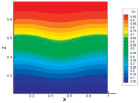
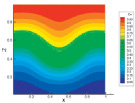
а б c
Рис. 4. Динамика изменения концентрации по времени для системы 0,5312Ar + 0,4688He – N2 при р = 2,0 МПа: а – t = 0,25; b – t = 1; c – t = 2
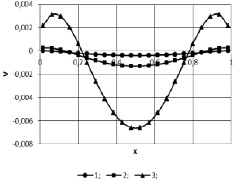
Рис. 5. Профиль скорости V(х) в сечении y = 0,5 в момент времени t = 2: 1 – р = 0,5 МПа; 2 – р = 1,5 МПа; 3 – р = 2,0 МПа
На рис. 4 при р = 2,0 МПа в система наблюдается срыв диффузионного процесса. Как видно, амплитуда колебаний концентрации увеличилась, что свидетельствует о нарушении условия устойчивости механического равновесия.
На рис. 5 приведен профиль скорости в сечении у = 0,5, который показывает изменение профиля вертикальной скорости при увеличении давления. Профиль скорости при давлении 2,0 МПа, что свидетельствует о возникновение конвективных течений [10].
Таким образом, проведенные исследования показали, что возникновение неустойчивости механического равновесия в тройной газовой смеси происходит при определенном значении критического давления p*. При p < p* в системе происходит диффузионный процесс.

