Принцип Ле-Шателье – Самуэльсона для открытой модели Леонтьева описывает как изменяется выпуск экономической системы при увеличении конечного спроса на один из продуктов системы, a уровень выпуска некоторой группы продуктов остается неизменным, при условии, что экономическая система является продуктивной. Классическая теорема, описывающая данный принцип, была установлена в предположении, что матрица прямых затрат является положительной матрицей [1], что с экономической точки зрения является очень жестким ограничением. Положительность матрицы прямых затрат означает, что каждая отрасль использует в производстве продукты всех отраслей. Очевидно, что это предположение далеко от действительности. Представляет интерес выяснить, сохраняется ли принцип Ле-Шателье – Самуэльсона для продуктивных экономических систем с неотрицательными матрицами. В данной статье показывается, что принцип Ле-Шателье – Самуэльсона остается верным и для более широкого класса экономических систем, a именно для систем с неразложимой матрицей прямых затрат, и приводится аналог этого утверждения для систем с произвольной неотрицательной матрицей прямых затрат.
Рассмотрим открытую модель Леонтьева, которая описывает экономическую систему, состоящую из некоторого числа отраслей и производящую некоторые набор продуктов, [2]. Обозначим число отраслей через n. В модели Леонтьева предполагается, что каждая отрасль выпускает единственный продукт, и каждый продукт выпускается единственной отраслью. Такие отрасли называются чистыми. Значит, рассматриваемая экономическая система состоит из n чистых отраслей и производит n продуктов, используя при этом для производства только продукты собственной системы. Экономическая система является открытой в том смысле, что существует конечный спрос потребителей. Основной целью функционирования системы является удовлетворение конечного спроса, т.е. производства такого набора продуктов, которого было бы достаточно и на производственное потребление внутри системы, и на конечный спрос потребителей. Последнее утверждение описывается следующим балансовым соотношением:
валовый выпуск = производственное потребление + конечный спрос. (1)
Введем следующие обозначения. Пусть xj – объем выпуска j-го продукта в j-й отрасли, cj – спрос потребителей на j-й продукт. Тогда вектор x = (x1, …, xn) – это вектор валового выпуска экономической системы, вектор c = (c1, …, cn) – вектор конечного потребления. Обозначим через aij – нормы производственного потребления на единицу выпускаемой продукции, т.е. количество i-го продукта, необходимого для производства единицы j-го продукта. В классической модели Леонтьева эти величины являются постоянными и не зависят от объема производства и времени, т.е. классическая модель Леонтьева является статической. Неотрицательные числа aij (i, j = 1, …, n) называются коэффициентами прямых затрат. Неотрицательная матрица A = (aij), составленная из этих элементов, называется матрицей прямых затрат. Матрица прямых затрат описывает технологию производства экономической системы. Тогда баланс затрат и выпуска экономической системы выражается уравнением:
x = Ax + c. (2)
Важным свойством экономической системы, описываемой моделью Леонтьева, является продуктивность. Экономическая система называется продуктивной, если она способна удовлетворить любой конечный спрос. В этом случае система может произвести некоторый неотрицательный набор продуктов x, который позволит удовлетворить заданный конечный спрос c. Экономическое свойство продуктивности математически означает, что система (2) имеет неотрицательное решение x ≥ 0 для любого неотрицательного вектора c ≥ 0. Легко видеть, что продуктивность экономической системы с матрицей прямых затрат A, эквивалентна существованию и неотрицательности матрицы (E – A)–1. А последнее имеет место тогда и только тогда, когда имеет место неравенство ρ(A) < 1, где ρ(A) – спектральный радиус матрицы A, [1].
Принцип Ле-Шателье – Самуэльсона описывает, как реагирует выпуск экономической системы на увеличение конечного спроса на какой-то продукт при фиксированном валовом выпуске некоторой группы продуктов. Пусть увеличивается спрос на некоторый продукт j, a уровень выпуска продуктов группы U должен оставаться неизменным, U – это множество индексов таких продуктов. Без ограничения общности можно считать, что U – это группа первых индексов. Тогда разобьем вектора x, c и матрицу A на три компоненты: первая соответствует продуктам из группы U, вторая – это одномерная часть j, третья отвечает оставшимся координатам W = {1, …, n}\({j} ∪ U): т.е. x = (u, v, w), c = (f, g, h), A = (Aij), i, j = 1, 2, 3. Тогда основное балансовое уравнение модели Леонтьева (2) можно переписать в виде системы трех уравнений:
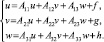(3)
Рассмотрим и сравним три решения системы (3):
● первоначальное решение системы x(c) = (u, v, w) – валовый выпуск системы, отвечающий первоначальному спросу c = (f, g, h),
● решение x(c′) = (u′, v′, w′), соответствующее конечному спросу с увеличенным спросом на продукт j, a именно c′ = (f, g′, h), g′ > g,
● решение x(c″) = (u, v″, w″), получаемое при увеличении спроса на j-й продукт и фиксированном выпуске продуктов группы U, соответствующее конечному спросу c″ = (f′, g′, h), g′ > g, компонента f при этом также меняется.
Известная теорема Ле-Шателье – Самуэльсона утверждает, что если матрица A положительна, то справедливы неравенства v″ < v и w″ < w, [1]. Оказывается, что утверждение этой теоремы верно и для неразложимых матриц. Напомним, что неотрицательная матрица A называется неразложимой, если ее нельзя путем перестановок строк и столбцов привести к виду:
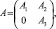
где A1, A2, A3 – ненулевые неотрицательные матрицы. В противном случае матрица называется разложимой [1].
Теорема 1. Пусть экономическая система, описываемая уравнением (2), продуктивна, и матрица прямых затрат A неразложима. Тогда увеличение выпуска любого продукта, вызванное увеличением конечного спроса на j-й продукт, в том случае, когда поддерживается постоянным выпуск продуктов группы U, оказывается меньшим, чем в случае, когда выпуск продуктов группы U не фиксируется.
Представляет интерес выяснить, что происходит в общем случае, т.е. для экономических систем с произвольной неотрицательной матрицей прямых затрат. Рассмотрим теперь случай, когда матрица прямых затрат A разложима.
Введем следующие обозначения. Пусть U – некоторая группа продуктов. Обозначим через PU(j) – множество всех продуктов из группы U, которые непосредственно (прямо) используются в j-й отрасли для производства j-го продукта, включая сам продукт j, т.е.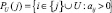 
. Обозначим через LU(j) – множество всех продуктов из группы U, которые косвенно используются в j-й отрасли для производства j-го продукта, включая сам продукт j, т.е. LU(j) – это множество индексов 
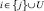, для каждого из которых можно указать цепочку 
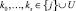такую, что k0 = i, ks = j и 
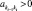при t = 1,…,s. Если J – это некоторое множество продуктов, то LU(J) – множество всех продуктов из группы U, которые косвенно используются для производства продуктов группы J. Теперь можно сформулировать аналог принципа Ле-Шателье – Самуэльсона для произвольных продуктивных экономических систем, без требования неразложимости матрицы прямых затрат.
Теорема 2. Пусть экономическая система, описываемая уравнением (2), является продуктивной. Тогда увеличение выпуска продукта i, вызванное увеличением конечного спроса на j-й продукт, в том случае, когда поддерживается постоянным выпуск продуктов группы U оказывается меньшим, чем в случае, когда выпуск продуктов группы U не фиксируется, если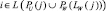 
.
Подробное доказательство этих утверждений приведено в совместной работе автора с П.П. Забрейко [2].
Таким образом, приведенные утверждения показывают, что принцип Ле-Шателье – Самуэльсона остается справедливым и для экономических систем с неразложимой матрицей прямых затрат. А также приводится аналог этого принципа и для более широкого класса продуктивных экономических систем. Следует отметить, что концепция модели Леонтьева и рассмотренный принцип Ле-Шателье – Самуэльсона может быть использован при принятии управленческих решений на макроуровне [4], и в целом при планировании и управлении экономическими системами [5].