Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Иванов В.В. 1

---

1 Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова АО «ОКТБ «ОРИОН»

Обсуждается возможное «гиперпространственное» представление структурных состояний объема [(r r r), (n n n), (f f f)3D conf, (f f f)*size, ((r r r)f + (n n n)f)site] композиционного материала для анализа величины эффективного размерного параметра. Представление включает символьные описания структурных состояний кристаллической (r r r) и наноразмерной (n n n) компонент, вероятных квазифрактальных конфигураций межфазных границ (f f f)3D conf, квазифрактальных size-распределений (f f f)*size и site-распределений ((r r r)f + (n n n)f)site элементов в объеме композита. Предполагается, что некоторые из проанализированных вариантов комплексных состояний могут быть результатом реализации определенного фазово-разупорядоченного состояния композиционных материалов и использованы при оценке величины синергического эффекта проявления антифрикционных свойств компонентами композита при трении и износе.

Статья в формате PDF

0 KB

структурные состояния

композиционные материалы

кристаллическая и наноразмерная компоненты

квазифрактальные конфигурации межфазных границ

site-распределения фаз

size-распределения

фазово-разупорядоченное состояние

1. Дерлугян П.Д., Иванов В.В., Иванова И.В. и др. Фрактальные структуры 2D пространства как возможные аппроксиманты конфигураций межфазных границ и распределения фаз на поверхности антифрикционных композиционных покрытий // Соврем. наукоемкие технологии. – 2013.- №.9. – С.86–88.

2. Иванов В.В. Фрактальные структуры как возможные абстракции сайз-распределения фаз и конфигурации межфазных границ на поверхности антифрикционных композиционных покрытий // Междунар. журнал прикладных и фундаментальных исследований. – 2013. – №10(3). – С.493–494.

3. Иванов В.В. Формирование фрактальных структур на основе итерационной последовательности и канторова множества точек с заданными характеристиками в 1D-пространстве // Успехи современного естествознания. – 2013. – № 8. – С. 136–137.

4. Иванов В.В. Возможные структурные состояния детерминистических модулярных структур с фрактальной компонентой в 3D пространстве // Успехи современного естествознания. – 2014. – № 4. – С. 105–108.

5. Иванов В.В. Размерные характеристики возможных состояний многокомпонентных структур, включающих фрактальную и наноразмерную компоненту // Успехи соврем. естествознания. – 2014. – №.7. – С.121–123.

6. Иванов В.В. Возможные состояния модулярных структур кристаллических, наноразмерных и фрактальных объектов на поверхности антифрикционных композиционных покрытий // Соврем. наукоемкие технологии, 2015. – № 8. – С.24–27.

7. Иванов В.В. Возможные состояния распределения модулярных структур кристаллических, наноразмерных и фрактальных объектов в объеме антифрикционных композиционных материалов // Соврем. наукоемкие технологии. – 2015. – № 5. – С.16–19.

8. Иванов В.В., Демьян В.В., Таланов В.М. Эволюционная модель формирования и анализ детерминистических фрактальных решеток // Успехи современного естествознания. – 2012. – № 4. – С. 230–232.

9. Иванов В.В., Таланов В.М. Разбиение и структурирование пространства, описание процесса формирования модульного кристалла // Успехи соврем. естествознания. – 2012. – №8. – С.75–77.

10. Иванов В.В., Таланов В.М. Разбиение структурированного 3D пространства на модулярные ячейки и моделирование невырожденных модулярных структур // Успехи соврем. естествознания. – 2012. – №10. – С.78–80.

11. Ivanov V.V. Possible states of the modular structures with nano-dimensional component into compositional coatings with anti-frictional properties // Eastern European Scientific Journal. – 2016. – N.1 – pp. 192–195.

12. Ivanov V.V. “Concentration waves” model for the tribologic system CM1/LL,о/CM2 // International journal of experimental education. – 2014. – № 4. – Part 2. – p.58–59.

13. Ivanov V.V. “Concentration waves” model for the tribologic system CM1/о/CM2 // International journal of experimental education. – 2014. – № 4. – Part 2. – p.59–60.

14. Ivanov V.V. Analysis of synergic effect in compositional coatings with taking into consideration the solid component of the counter-body and the liquid lubricant // European Journal of Natural History. – 2015. – № 3. – С.36–37.

15. Ivanov V. V., Derlugian P.D., Ivanova I.V., et al. Fractal structures as a possible abstractions of the site and size-distributions of phases and a possible approximants of the inter-phase borders configurations onto surface of the composites // Eastern European Scientific Journal. – 2016. – N.2 – pp. 203–206.

16. Ivanov V. V., Derlugian P.D., Ivanova I.V., et al. Ultradispersoids as the modificators for some compositional coatings // Eastern European Scientific Journal. – 2016. – N. 2 – pp. 207–210.

17. Ivanov V.V., Ivanova I.V. Structural states of the surface of compositional coatings with nano-dimensional and fractal components // Eastern European Scientific Journal. – 2016. – N.1 – pp. 195–198.

18. Shcherbakov I. N., Ivanov V.V. Analysis of synergic effect in compositional Ni-P-coatings // European Journal of Natural History. – 2015. – № 3. – С.48.

19. Shcherbakov I.N., Ivanov V.V. Multilayered composite solid lubricating coating // Eastern European Scientific Journal. – 2016, – N.2 – pp. 199–202.

В 3D пространстве, структурированном с помощью разбиения его на модулярные ячейки, возможно формирование невырожденных модулярных структур [9, 10]. В ячейках такого пространства реализуются структурные состояния в общем случае с кристаллической, наноразмерной и фрактальной компонентами [1–4, 6, 7, 15–17]. Образы сечений подобных структур рассматривали как возможные аппроксиманты вероятных сайз-распределений фаз и квазифрактальных конфигураций межфазных границ на поверхности композитов [1, 2, 15, 16]. Определены размерные характеристики возможных многокомпонентных структурных состояний систем [5].

В [6, 7] для описания комплексного структурного состояния объема композита предложено учитывать состояния классов (r r r), (n n n) и некоторые фрактальные компоненты класса (f f f). Однако, при этом не учитывали возможное влияние состояний в гиперобъеме материала на комплексное структурное состояние композита, в частности, на условный размерный параметр поверхности, что является целью данной работы. Для достижения этой цели необходимо решить следующие задачи:

1) описание объемных структурных состояний, указанных в 15-мерном («гиперпространственном») представлении и определение размерного параметра <D>,

2) определение влияния дополнительных по отношению к объему возможных компонент гиперобъёмных структурных состояний на размерный параметр <D>.

Проанализируем некоторые особенности «гиперпространственного» представления структурных состояний композитов и методику определения объемного размерного параметра с учетом возможного гиперобъемного состояния этого же материала.

«Гиперпространственное» представление объемных структурных состояний

В общем случае методика «гиперпространственного» представления возможных структурных состояний (15-мерной в объеме материала [(r r r), (n n n), (f f f)3D conf, (f f f)*size, ((r r r)f + (n n n)f)site]) включает в себя следующие процедуры:

– описание структурных состояний из кристаллической (r r r) и наноразмерной (n n n) компонент композита,

– описание вероятных квазифрактальных конфигураций межфазных границ (f f f)3Dconf, которые являются 3D оболочками системы элементов детерминистических модулярных структур с соответствующими фрактальными состояниями,

– описание вероятных квазифрактальных 3D распределений элементов по позициям детерминистических модулярных структур (описания site-распределений (f f f)site = (f f f)*),

– описание вероятных квазифрактальных 3D распределений элементов r и n по размерам (описания size-распределений в объеме композита (r r r)f, size и (n n n)f, size).

Приведем пример выбора необходимых для анализа объемных структурных состояний некоторого кристаллического наноразмерного квазифрактального объекта в виде 5х10–матрицы:

.

Приведем подробные описания указанных в матрице 3D состояний.

1. Класс кристаллический, подкласс P состояния (r r r):

(r r r) – 3D кристалл из упорядоченных в объеме и слоях цепочек асимметричных модулей,

(r r rn) – 3D кристалл из упорядоченных цепочек нанофрагментов и слоев асимметричных модулей,

(r r rf) – 3D кристалл из упорядоченных цепочек локальных фракталов и слоев асимметричных модулей,

(r rn rn) – 3D кристалл из упорядоченных в слое цепочек нанофрагментов и цепочек асимметричных модулей,

(r rn rf) – 3D кристалл из упорядоченных цепочек локальных фракталов, нанофрагментов и асимметричных модулей,

(r rf rf) – 3D кристалл из упорядоченных в слое цепочек локальных фракталов и цепочек асимметричных модулей,

(rn rn rn) – 3D кристалл из упорядоченных в объеме и слоях цепочек нанофрагментов,

(rn rn rf) – 3D кристалл из упорядоченных в слое цепочек нанофрагментов и цепочек локальных фракталов,

(rn rf rf) – 3D кристалл из упорядоченных в слое цепочек локальных фракталов и цепочек нанофрагментов,

(rf rf rf) – 3D кристалл из упорядоченных в объеме и слоях цепочек локальных фракталов.

2. Класс наноразмерный, подкласс N состояния (n n n):

(n n n) – 3D нанообъект из из упорядоченных в объеме и слоях цепочек наночастиц,

(n n nr) – 3D нанообъект из упорядоченных цепочек нанофрагментов и слоев наночастиц,

(n n nf) – 3D нанообъект из упорядоченных цепочек нанофракталов и слоев наночастиц,

(n nr nr) – 3D нанообъект из упорядоченных в слое цепочек нанофрагментов и цепочек наночастиц,

(n nr nf) – 3D нанообъект из упорядоченных цепочек нанофрагментов, нанофракталов и наночастиц,

(n nf nf) – 3D нанообъект из упорядоченных в слое цепочек нанофракталов и цепочек наночастиц,

(nr nr nr) – 3D нанообъект из упорядоченных в объеме и слоях цепочек нанофрагментов,

(nr nr nf) – 3D нанообъект из упорядоченных в слое цепочек нанофрагментов и цепочек нанофракталов,

(nr nf nf) – 3D нанообъект из цепочек нанофрагментов структуры и упорядоченных в слое цепочек нанофракталов,

(nf nf nf) – 3D нанообъект из упорядоченных в объеме и слоях цепочек нанофракталов.

3. Класс гибридный фрактальный, подкласс F состояния (f f f):

(f f f) – 3D фрактальный объект из упорядоченных в объеме и слоях цепочек асимметричных фракталов,

(f f fr) – 3D фрактальный объект из упорядоченных в слое цепочек асимметричных фракталов и цепочек фрактальных фрагментов,

(f f fn) – 3D фрактальный объект из упорядоченных в слое цепочек асимметричных фракталов и цепочек наноструктурированных фракталов,

(f fr fr) – 3D фрактальный объект из упорядоченных в слое цепочек фрактальных фрагментов и цепочек асимметричных фракталов,

(f fr fn) – 3D фрактальный объект из упорядоченных в объеме цепочек фрактальных фрагментов, наноструктурированных фракталов и асимметричных фракталов,

(f fn fn) – 3D фрактальный объект из упорядоченных в слое цепочек наноструктурированных фракталов и цепочек асимметричных фракталов,

(fn fr fr) – 3D фрактальный объект из упорядоченных в слое цепочек фрактальных фрагментов и цепочек наноструктурированных фракталов,

(fr fr fr) – 3D фрактальный объект из упорядоченных в объеме слоев из цепочек фрактальных фрагментов,

(fr fn fn) – 3D фрактальный объект из упорядоченных в слое цепочек наноструктурированных фракталов и цепочек фрактальных фрагментов,

(fn fn fn) – 3D фрактальный объект из упорядоченных в объеме слоев из цепочек наноструктурированных фракталов.

4. Класс сопряженный гибридному фрактальному, подкласс F* состояния (f f f)*:

(f f f) – 3D фрактальный объект из упорядоченных в объеме и слоях цепочек асимметричных фракталов,

(f f rf) – 3D фрактальный объект из упорядоченных в слоях цепочек асимметричных фракталов и цепочек локальных фракталов,

(f f nf) – 3D фрактальный объект из упорядоченных в слоях цепочек асимметричных фракталов и цепочек нанофракталов,

(f rf rf) – 3D фрактальный объект из упорядоченных в слое цепочек локальных фракталов и цепочек асимметричных фракталов,

(f rf nf) – 3D фрактальный объект из упорядоченных в объеме цепочек локальных фракталов, нанофракталов и асимметричных фракталов,

(f nf nf) – 3D фрактальный объект из упорядоченных в слое цепочек нанофракталов и цепочек асимметричных фракталов,

(nf rf rf) – 3D фрактальный объект из упорядоченных в слое цепочек локальных фракталов и цепочек нанофракталов,

(rf rf rf) – 3D фрактальный объект из упорядоченных в объеме цепочек локальных фракталов,

(rf nf nf) – 3D фрактальный объект из упорядоченных в слое цепочек нанофракталов и цепочек локальных фракталов,

(nf nf nf) – 3D фрактальный объект из упорядоченных в объеме цепочек нанофракталов.

5. Класс наноразмерный, подкласс N, только состояния (n n n)f:

(n n nf) – 3D нанообъект из слоев наночастиц и наночастиц, упорядоченных в цепочке по фрактальному закону,

(n nr nf) – 3D нанообъект из нанофрагментов структуры и наночастиц, упорядоченных в цепочке по фрактальному закону,

(n nf nf) – 3D нанообъект из наночастиц, упорядоченных в слоях по фрактальному закону,

(nr nr nf) – 3D нанообъект из упорядоченных в слоях цепочек нанофрагментов и наночастиц, упорядоченных в цепочке по фрактальному закону,

(nr nf nf) – 3D нанообъект из цепочек нанофрагментов структуры и наночастиц, упорядоченных в слоях по фрактальному закону.

6. Класс кристаллический, подкласс P, только состояния (r r r)f:

(r r rf) – 3D кристалл из слоев асимметричных модулей и модулей, упорядоченных в цепочке по фрактальному закону,

(r rn rf) – 3D кристалл из асимметричных модулей, нанофрагментов и асимметричных модулей, упорядоченных в цепочке по фрактальному закону,

(r rf rf) – 3D кристалл из асимметричных модулей, упорядоченных в слоях по фрактальному закону,

(rn rn rf) – 3D кристалл из упорядоченных в слоях цепочек нанофрагментов и асимметричных модулей, упорядоченных в цепочках по фрактальному закону,

(rn rf rf) – 3D кристалл из цепочек нанофрагментов и асимметричных модулей, упорядоченных в слоях по фрактальному закону.

Дополнительными по отношению к поверхности возможными компонентами объемных структурных состояний могут быть следующие 1D объекты:

.

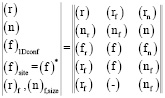Приведем подробные описания указанных в матрице состояний 1D объектов с указанием их класса.

1. Класс кристаллический, подкласс P состояния (r):

(r) – 1D кристалл из упорядоченных в цепочке асимметричных модулей,

(rn) – 1D кристалл из упорядоченных в цепочке нанофрагментов,

(rf) – 1D кристалл из упорядоченных в цепочке локальных фракталов.

2. Класс наноразмерный, подкласс N состояния (n):

(n) – 1D нанообъект из упорядоченных в цепочке наночастиц,

(nr) – 1D нанообъект из упорядоченных в цепочке нанофрагментов структуры,

(nf) – 1D нанообъект из упорядоченных в цепочке нанофракталов.

3. Класс фрактальный, подкласс F состояния (f):

(f) – 1D фрактальный объект из упорядоченных в цепочке асимметричных фракталов,

(fr) – 1D фрактальный объект из упорядоченных в цепочке фрактальных фрагментов,

(fn) – 1D фрактальный объект из упорядоченных в цепочке наноструктурированных фракталов.

4. Класс сопряженный фрактальному, подкласс F* состояния (f)*:

(f) – 1D фрактальный объект из упорядоченных в цепочке асимметричных фракталов,

(rf) – 1D фрактальный объект из упорядоченных в цепочке локальных фракталов,

(nf) – 1D фрактальный объект из упорядоченных в цепочке нанофракталов.

5. Класс наноразмерный, подкласс N, только состояния (n)f:

(nf) – 1D нанообъект из наночастиц, упорядоченных в цепочке по фрактальному закону.

6. Класс кристаллический, подкласс P, только состояния (r)f:

(rf) – 1D кристалл из асимметричных модулей, упорядоченных в цепочке по фрактальному закону.

Формальный учет этих дополнительных состояний для объема означает гиперпространственную поправку, т.е. учет влияния на размерный параметр <D> гиперобъемной характеристики структурного состояния материала:

Необходимые структурные состояния кристаллического (r r r r), наноразмерного (n n n n), гибридного фрактального (f f f f) и сопряженного с ним (f f f f)* класса могут быть перечислены в соответствии с методикой, аналогичной представленной в [6, 7].

Условный размерный параметр Di для каждого i-го структурного 4D состояния может быть рассчитан по формуле Di = 0,5(dr D(r) + df D(f) + dn D(n))i, где dr, df и dn – количества соответствующих компонент одного сорта. Значения для кристаллической компоненты D(r) = 1, для фрактальной компоненты совпадают с фрактальной размерностью: D(f) = DimRf = Dim (GenRf) < 1, для наноразмерной компоненты D(n) = (<n>/no) < 1, если средний размер нанообъекта <n> меньше, чем no = 100 нм [5].

Пример методики расчета размерного параметра <D>. Предположим, что для структурного 3D состояния объема некоторого композита

[(rn rf rn), (nn nf nn), (fr fn fn)3D conf, (rf nf nf)site, (rn rf rf)f,(nn nf nf)f size]

и связанного с ним 4D состояния в гиперобъеме

[(rn rf rn rf), (nn nf nn nf), (fr fn fn fr)4D conf, (rf nf nf nf)site, (rn rf rf rf)f,(nn nf nf nf)f size]

имеем:

– среднее значение параметра для 3D состояния

<D>3D = (1/12)(8 D(r) + 16 <D(n)> + +12 <D(f)>) = (2/3) + (4/3) <D(n)1> + +<D(f)2>,

– среднее значение параметра для 4D состояния

<D>4D = (1/12)(11 D(r) + 19<D(n)> + +18<D(f)>) = (11/12) + (19/12)<D(n)1> + +(3/2)<D(f)2>.

Тогда среднее значение параметра только для четвертых координат 4D состояния

<D>1D = (1/12)(3 D(r) + 3 <D(n)> + +6 <D(f)>) = (1/4) + 0,25 <D(n)2> + + (1/2) <D(f)3>,

а среднее значение параметра для объема с учетом гиперобъемной поправки

<Dобъема> = (2/3)(<D>3D + <D>1D).

Таким образом, в зависимости от возможного «продолжения» композиционного материала (кристаллическое, наноразмерное или квазифрактальное) в четвертом («гиперпространственном») измерении эффективное значение размерного параметра <Dобъема> может отличаться от формального значения <D>3D. Отметим, что результаты анализа возможных видов структурных состояний и оценка размерного параметра необходимы для учета его возможного влияния на некоторые аддитивные свойства соответствующего композиционного материала. В частности, отклонение значения параметра для анализируемого многофазного объекта от величины мерности пространства, в котором этот объект существует, может обусловить эффект синергизма свойств функциональных компонентов, например, твердой и смазочной компоненты трибологических свойств антифрикционных композиционных покрытий [12–14, 18, 19].

Выводы

Рассмотрено возможное «гиперпространственное» представление структурных состояний объема [(r r r), (n n n), (f f f)3D conf, (f f f)*size, ((r r r)f + (n n n)f)site] композиционного материала для анализа величины эффективного размерного параметра, определяющего отклонение аддитивных поверхностных свойств материалов от соответствующих его объемных свойств. Предполагается, что некоторые из проанализированных вариантов комплексных состояний могут быть результатом непрерывной реализации определенного фазово-разупорядоченного состояния композиционных материалов и использованы при оценке величины синергического эффекта проявления антифрикционных свойств компонентами композита при трении и износе.

Библиографическая ссылка