Рассматриваются вопросы численного моделирования взрывного воздействия на упругую полуплоскость с полостью. Поставленная задача решается с помощью численного моделирования уравнений нестационарной математической теории упругости.
Волны напряжений различной природы, распространяясь, в деформируемом теле взаимодействуют, друг с другом. При интерференции волн напряжений их интенсивности складываются. Они могут достигать значений, превосходящих предел прочности материала. В этом случае наступает разрушение материала. После трехкратного или четырехкратного прохождения и отражения волн напряжений в теле процесс распространения возмущений становится установившимся, напряжения и деформации усредняются, тело находится в колебательном движении.
Некоторые вопросы в области моделирования нестационарных динамических задач с помощью применяемого метода, алгоритма и комплекса программ рассмотрены в следующих работах [1–10].
Постановка задачи с начальными и граничными условиями
Для решения задачи о моделировании упругих нестационарных волн напряжений в деформируемых областях сложной формы рассмотрим некоторое тело Г в прямоугольной декартовой системе координат XOY, которому в начальный момент времени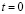 
сообщается механическое нестационарное импульсное воздействие.
Предположим, что тело Г изготовлено из однородного изотропного материала, подчиняющегося упругому закону Гука при малых упругих деформациях.
Точные уравнения двумерной (плоское напряженное состояние) динамической теории упругости имеют вид
, 
,
,
,
, 
,
, 
, 
,
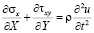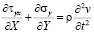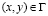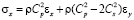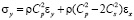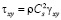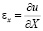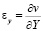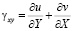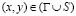, (1)
где 
, 
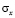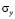и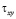 
– компоненты тензора упругих напряжени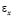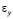й; 
, 
и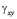 
– компоненты тензора упругих деформаций; u и v – составляющие вектора упругих перемещений вдоль осей OX и OY соответственно; 
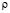– плотность материала; 
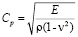– скорость продольной упругой волны; 
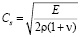– скорость поперечной упругой волны; 
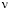– коэффициент Пуассона; E – модуль упругости; 
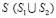– граничный контур тела Г.
Систему (1) в области, занимаемой телом Г, следует интегрировать при начальных и граничных условиях.
Разработка методики и алгоритма
Для решения двумерной плоской динамической задачи теории упругости с начальными и граничными условиями (1) используем метод конечных элементов в перемещениях.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Г, записываем приближенное значение уравнения движения в теории упругости
, 
,
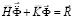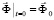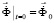, (2)
где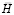 
– диагональная матрица инерции; 
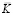– матрица жесткости; 
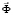– вектор узловых упругих перемещений; 
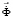– вектор узловых упругих скоростей перемещений; 
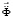– вектор узловых упругих ускорений; 
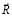– вектор внешних узловых упругих сил.
Соотношение (2) система линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями.
Таким образом, с помощью метода конечных элементов в перемещениях, линейную задачу с начальными и граничными условиями (1) привели к линейной задаче Коши (2).
Для интегрирования уравнения (2) конечноэлементным вариантом метода Галеркина приведем его к следующему виду
, 
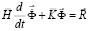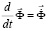. (3)
Интегрируя по временной координате соотношение (3) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
,
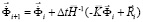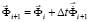, (4)
где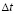 
– шаг по временной координате.
Основные соотношения метода конечных элементов в перемещениях получены с помощью принципа возможных перемещений и конечноэлементного варианта метода Галеркина.
Общая теория численных уравнений математической физики требует для этого наложение определенных условий на отношение шагов по временной координате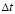 
и по пространственным координатам, а именно
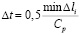
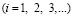, (5)
где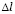 
– длина стороны конечного элемента.
Для исследуемой области, состоящей из материалов с разными физическими свойствами, выбирается минимальный шаг по временной координате (5).
В работах [1, 4, 6, 9–10] приведена информация о физической достоверности и математической точности моделирования нестационарных волн напряжений в деформируемых телах с помощью рассматриваемого численного метода, алгоритма и комплекса программ.
Численное моделирование нестационарных волн напряжений
Расчеты проводились при следующих единицах измерения: килограмм-сила (кгс); сантиметр (см); секунда (с). Для перехода в другие единицы измерения были приняты следующие допущения:
1 кгс/см2 * 0,1 МПа; 1 кгс с2/см4 * 109 кг/м3.
Рассмотрим задачу о воздействии сосредоточенной взрывной волны на свободной поверхности упругой полуплоскости с полостью (соотношение ширины к высоте один к четырем) (рис. 1). В точке F перпендикулярно свободной поверхности ABEFG приложено сосредоточенное нормальное напряжение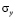 
(рис. 1), которое при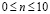 
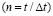изменяется линейно от 0 до P, а при 
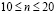от P до 0 (
, 
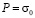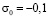МПа (–1 кгс/см2)). Граничные условия для контура GHIA при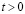 
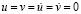. Отраженные волны от контура GHIA не доходят до исследуемых точек при 
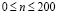. Контур ABCDEFG свободен от нагрузок, кроме точки F, где приложено сосредоточенное упругое нормальное напряжение 
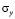. Расчеты проведены при следующих исходных данных: 
; 
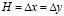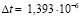с; E = 3,15*10 4 МПа (3,15*10 5 кгс/см2); n= 0,2; r= 0,255*104 кг/м3 (0,255*10-5 кгс•с2/см4); Cp= 3587 м/с; Cs = 2269 м/с. Решается система уравнений из 59048 неизвестных.
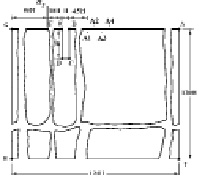
Рис. 1. Постановка задачи о воздействии сосредоточенной взрывной волны на свободной поверхности упругой полуплоскости с полостью (соотношение ширины к высоте один к четырем)
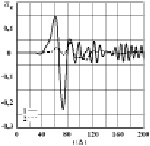
Рис. 2. Изменение упругого контурного напряжения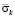 
во времени 
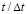в точке A1: 1 – в задаче без полости; 2 – в задаче с полостью (соотношение ширины к высоте один к четырем)
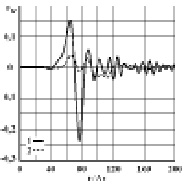
Рис. 3. Изменение упругого контурного напряжения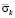 
во времени 
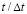в точке A2: 1 – в задаче без полости; 2 – в задаче с полостью (соотношение ширины к высоте один к четырем)
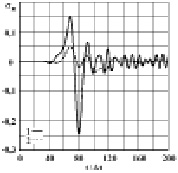
Рис. 4. Изменение упругого контурного напряжения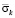 
во времени 
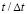в точке A3: 1 – в задаче без полости; 2 – в задаче с полостью (соотношение ширины к высоте один к четырем)
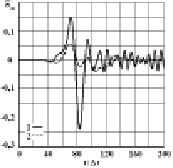
Рис. 5. Изменение упругого контурного напряжения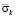 
во времени 
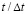в точке A4: 1 – в задаче без полости; 2 – в задаче с полостью (соотношение ширины к высоте один к четырем)
Результаты расчетов для контурного напряжения 
(
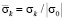) во времени n получены в точках A1–A4 (рис. 1), находящихся на свободной поверхности упругой полуплоскости.
На рис. 2–5 приведены контурные напряжения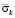 
во времени n, которые получены в точках A1–A4 .
Выводы
Для оценки несущей способности и прогноза безопасности уникальных сооружений при взрывных воздействиях применяется численное моделирование. На основе метода конечных элементов в перемещениях разработаны методика, алгоритм и комплекс программ для решения линейных двумерных плоских задач, которые позволяют решать сложные задачи при взрывных воздействиях на сооружения. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений. Матрица упругости выражена через скорость продольных волн, скорость поперечных волн и плотность.
Исследуемая область разбивается по пространственным переменным на треугольные конечные элементы с тремя узловыми точками с линейной аппроксимацией упругих перемещений и на прямоугольные конечные элементы с четырьмя узловыми точками с билинейной аппроксимацией упругих перемещений. По временной переменной исследуемая область разбивается на линейные конечные элементы с двумя узловыми точками с линейной аппроксимацией упругих перемещений. За основные неизвестные приняты два перемещения и две скорости перемещений в узле конечного элемента.
Задачи решаются методом сквозного счета, без выделения разрывов. Применяется кусочно-линейная аппроксимация для уменьшения влияния разрывов на точность результатов численного решения, полученных с помощью метода конечных элементов в перемещениях.
Линейная динамическая задача с начальными и граничными условиями в виде дифференциальных уравнений в частных производных, для решения задач при взрывных воздействиях, с помощью метода конечных элементов в перемещениях приведена к системе линейных обыкновенных дифференциальных уравнений с начальными условиями, которая решается по явной двухслойной схеме.
На основании проведенных исследований можно сделать вывод о физической достоверности результатов численного решения полученных, с помощью метода конечных элементов в перемещениях, при решении задач о распространении взрывных волн в деформируемых телах.
Решена задача о воздействии сосредоточенной взрывной волны на свободной поверхности упругой полуплоскости с полостью (соотношение ширины к высоте один к четырем). Решается система уравнений из 59048 неизвестных. Рассматриваются точки на свободной поверхности упругой полуплоскости.
Полученные результаты показывают уменьшение напряжений при применении полости с соотношением ширины к высоте один к четырем.
Полученные результаты можно оценить как первое приближение к решению сложной комплексной задачи, о применении полостей для увеличения безопасности уникальных объектов по несущей способности (прочности) при взрывных воздействиях, с помощью численного моделирования волновых уравнений теории упругости.
Библиографическая ссылка
Мусаев В.К. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ НЕСТАЦИОНАРНЫХ ВОЛН НАПРЯЖЕНИЙ В УПРУГОЙ ПОЛУПЛОСКОСТИ С ПОЛОСТЬЮ (СООТНОШЕНИЕ ШИРИНЫ К ВЫСОТЕ ОДИН К ЧЕТЫРЕМ) ПРИ СОСРЕДОТОЧЕННОМ ВЗРЫВНОМ ВОЗДЕЙСТВИИ // Международный журнал экспериментального образования. – 2016. – № 11-2. – С. 192-196;URL: https://expeducation.ru/ru/article/view?id=10856 (дата обращения: 23.04.2024).