Индустриальный характер мостостроения предопределяет применение как сборных элементов мостовых конструкций, так и комплектов инвентарных элементов вспомогательных сооружений. Использование временных опор из инвентарных конструкций при строительстве мостов получило широкое распространение ещё в СССР [3, 4, 11,33 и др.]. Необходимо отметить, что использование инвентарных конструкций широко практиковалось и за рубежом [33, 36, 42]. До конца семидесятых годов прошлого века наиболее эффективно использовались УИКМ (универсальные инвентарные конструкции для мостостроения) с многоболтовыми соединениями элементов в узлах.
К числу новых типов относятся конструкции с соединением на высокопрочных болтах типа МИК-С (мостовые инвентарные конструкции стоечного типа), МИК-П (мостовые инвентарные конструкции пакетного типа), ИПРС (инвентарные подмости ручной сборки) и СВСиУ (специальные временные сооружения и устройства для возведения городских мостовых сооружений).
Условия применения и принципы проектирования вспомогательных сооружений из инвентарных конструкций определяют ряд особенностей работы этих сооружений. К этим особенностям относятся податливость фундаментов стационарных опор, взаимодействие надстроек и плашкоутов плавучих опор, влияние на напряженное состояние надстроек усилий от жесткости узлов, а также перераспределение усилий в системах от податливости узлов и соединений.
В практике проектных организаций отмеченные особенности при выполнении расчетов вспомогательных сооружений, как правило, не учитываются. Это затрудняет проектирование равнопрочных конструкций и приводит как к наличию излишних запасов в одних элементах сооружения, так и к недостаточной надежности других.
Поэтому можно считать, что исследования, направленные на изучение действительной работы вспомогательных сооружений, продолжают является актуальными. Их проведение соответствует задачам технического прогресса в мостостроении.
Наиболее сложным вопросом расчета вспомогательных опор является определение усилий в элементах. Вспомогательные опоры представляют собой внутренне и внешне статически неопределимые решетчатые системы (в случае стационарных опор) или же сочетание таких систем с изгибаемыми балками или пластинками, представляющими плашкоуты плавучих опор. Существующая практика расчета вспомогательных опор основана на ряде предпосылок и допущений.
Например, при расчете надстройки на действие вертикальных сил полагается [27], что разность узловой нагрузки и опорной реакции (P1 – R1) по условию равновесия отсеченной части распределяется между раскосами поровну. Если количество раскосов, попадающих в разрез 1 – 1, равно n, то усилие в каждом из них определяется по формуле
.
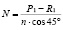Распределение опорных реакций в стойках нижней панели от действия моментов, вызванных горизонтальными и эксцентрично приложенными нагрузками, принимается по методу внецентренного сжатия:
,
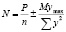где P – центрально приложенная вертикальная нагрузка; M – момент в плоскости низа опоры; n – число стоек; ymax – расстояние от оси опоры до крайней стойки.
Усилия в раскосах от горизонтальной нагрузки определяются исходя из условия, что поперечная сила распределяется между раскосами поровну.
В случае плавучих опор учитывается совместная работа решетчатой надстройки с плашкоутом, причем последний рассматривается, обычно, в качестве изгибаемой балки при узких или в качестве пластинки при относительно широких плашкоутах. В качестве нагрузки принимается гидростатическое давление. Расчет пластинки ведется по схеме балочного ростверка на податливых опорах с учетом упругих характеристик [48].
Определение усилий с учетом податливости стыков плашкоута в системах, у которых деформации распределительной конструкции и плашкоута связаны, производится путем введения в уравнение деформаций дополнительных перемещений по направлению каждого неизвестного. Податливость стыков плашкоута по методике СКБ Главмостостроя учитывается дополнительным прогибом плашкоута при возможном неупругом взаимном повороте двух понтонов в каждом стыке. Это смещение принимается равным 10 мм [32].
При расчете решетчатых надстроек могут быть использованы многочисленные работы, посвященные металлическим решетчатым каркасным конструкциям.
Использование ЭВМ привело к качественному скачку в техническом уровне расчетов каркасных конструкций и позволило перейти от расчетов отдельных плоских систем к расчету сооружения в целом. Рассмотрение всего сооружения как единой системы позволяет правильнее оценить его поведение под нагрузкой и получить более экономичное проектное решение.
Разработанные в ЦНИИПСК программы позволяют рассчитывать сложные многократно статически-неопределимые стержневые системы методом перемещений.
На базе матричного аппарата проведены многочисленные исследования по реализации на ЭВМ алгоритмов, основанных на классическом методе сил, методе перемещений, смешанном методе, а также на их модификациях. Анализ существующих программ расчета пространственных стержневых систем с указанием их возможностей выполнен в работе [5].
Одним из важных моментов, определяющих работу решетчатых каркасных конструкций, является учет работы сопряжений элементов, а также взаимодействия каркасной системы с фундаментами и основаниями. Заслуживает внимания работа [28] по учету совместной работы оснований фундаментов и поперечных рам промышленных зданий со стальным каркасом. Показано, что деформации оснований существенным образом сказывается на напряженном состоянии поперечных рам.
Основные закономерности по распределению усилий между каркасом и фундаментом с учетом их совместной работы с просадочным основанием, а также влияние конструкций и жесткости узлов каркаса на допустимую разность осадок соседних колонн освещены в работе [47].
Как известно, в основу статического расчета рамных систем вкладывается неизменяемость углов в каждом узловом соединении стоек и ригелей. При расчете конструкций из стрежневых элементов на устойчивость в работах [39] учитывается жесткость узловых соединений, так как не учет последней при одноболтовом соединении приводит к тому, что критическая сила уменьшается против действительной примерно в два раза.
Оценка влияния работы сопряжений стальных ригелей с колонными на распределение усилий в рамах дана в работе [41]. Автор предложил новую расчетную схему рам с упругоподатливыми узлами, а также методику расчета таких рам методом сил и методом деформаций. Расчет рам по методу сил сводится к составлению и решению канонических уравнений, в которых коэффициенты при неизвестных учитывают работу узлов, имеющих дополнительные упругие стержни с заданными коэффициентами податливости.
Упругая податливость узловых соединений в работе каркасов промышленных зданий эквивалентна уменьшению жесткостей ригелей.
В работе [29] упругую податливость узловых соединений при расчете стальных каркасов на деформативность учитывается путем введения приведенной жесткости ригеля, определяемой по формуле
,
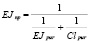где С – коэффициент жесткости узлового соединения, определяемый из прямой зависимости между величиною изгибающего момента на ригеле и углом поворота. В частности, указывается, что учет деформативности узловых соединений приводит к перераспределению напряженного состояния рамных стальных каркасов, а также к увеличению горизонтальных смещений на величину 20 % при расчете на ветровую нагрузку.
Существенное влияние деформативности фланцевых соединений на распределение усилий и деформаций в элементах рамы выявлено при проведении экспериментально-теоретических исследований, результаты которых приводятся в работах [6, 12, 34, 35]. Авторы установили зависимость деформации сопряжений и предельных усилий от основных геометрических размеров растянутых узлов, а также связь между деформациями сопряжений и распределением моментов в поперечной раме.
Необходимость учета деформативности сопряжений связана с тем, что законструированные жесткие узлы рамы в действительности деформативны, а шарнирные даже при минимальном конструктивном креплении способны воспринимать значительные моменты.
Экспериментально-теоретические исследования [40], проводившиеся в ЦНИИСКе им. Кучеренко на опорах ЛЭП с болтовыми соединениями показали, что податливость в болтовых соединениях статически неопределимых стержневых конструкций приводит к остаточным прогибам в системе, увеличению ее деформативности и к резкому перераспределению внутренних усилий. Податливость болтовых соединений при разнице диаметров болта и отверстия 3мм приводит к увеличению общих деформаций структурной конструкции на 40 % и изменению усилий в элементах до 20 %. В некоторых случаях усилия в элементах меняют знак. Степень влияния податливости болтового соединения каждого раскоса учитывается уменьшением площади его поперечного сечения путем введения в расчет фиктивной площади, определяемой по формуле:
,
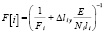где Ni – действующее усилие в элементе от внешней нагрузки; li – длина i-го элемента; Е – модуль упругости; Δlну – заданная (неупругая) податливость болтового соединения.
Для вычисления фиктивной площади вводится заданная податливость болтового соединения. При решении задачи с учетом податливости болтовых соединений авторы [25,40] считают, что деформативность пропорциональна усилию, т.е. деформации развиваются по линейному закону. В работах приводится только две стадии работы соединения, а именно: упругая деформация; СДВИГ – неупругая деформация, вызванная податливостью болтового соединения.
Применительно к мостовым конструкциям с клепаными соединениями вопросу смещения в соединениях и его влияния на перераспределение усилий в элементах статически неопределимых систем посвящены работы [28, 38, 43]. В работах [22 – 24] этот вопрос рассмотрен применительно к мостовым конструкциям с болтосрезными соединениями на высокопрочных болтах.
Повышенная деформативность соединений на высокопрочных болтах нашла отражение и в нормах проектирования этих соединений в США, основанных на данных многочисленных экспериментальных исследований, в том числе [49,50]. Указано, что из-за значительных смещений не допускается применение соединений данного типа при действии на конструкцию знакопеременных усилий.
Учет смещений в болтовых и клепаных соединениях металлических конструкций основывается на современном представлении о действительной работе данного соединения.
Общее решение задачи о напряженно-деформированном состоянии заклепочных и болтовых соединений при наличии сил трения дано в [43–46]. Решение дано при линейной зависимости между смещением и нагрузкой. Результаты теоретических [43] и экспериментальных [45,46] исследований показали, что между усилиями и деформациями в заклепочных соединениях существует нелинейная зависимость. Кроме того, в работе [43] указывается на наличие связи между деформациями сдвига и толщиной листов стягиваемых пакетов. Согласно [43], податливость прикреплений в заклепочных соединениях мостовых конструкций учитывается посредством изменения площади поперечного сечения элемента на коэффициент К, определяемый по формуле:
,
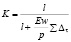где l – длина элемента; w – площадь поперечного сечения элемента; Р – усилие в элементе; Δτ – деформация заклепочного соединения.
В семидесятых годах для соединения элементов стальных конструкций во многих странах мира нашли применение высокопрочные болты.
Исследованиям действительной работы соединений с несущими болтами посвящено много работ. Следует отметить работу [7], в которой предложен вероятностный подход к расчету нормативных усилий натяжения высокопрочных болтов. Предложенная методика позволяет более правильно отразить в нормах проектирования несущую способность высокопрочных болтов во фрикционных соединениях мостовых конструкций.
В работе [8] приводится диаграмма деформативности одноболтового соединения, характеризующаяся тремя стадиями: упругая работа; сдвиг на разность диаметров болта и отверстия; работа соединения на смятие. Третья стадия имеет нелинейную связь между деформацией и усилием и выражается эмпирической зависимостью:
S(Δ) = (C1δ+C2δ2) ? + (C3δ+C4δ2) Δ2,
где:δ – приведенная толщина соединяемых фасонок в односрезном соединении; Сi – эмпирические параметры, дифференцированные по прочности материала соединяемых элементов.
При расчете статически неопределимых мостовых конструкций деформативность элементов с заклепочными и на высокопрочных болтах соединениями, согласно [26], учитывается посредством введения в расчет эквивалентных жесткостей элементов (EF)э, при которых упругое удлинение элементов равно увеличению расстояния между центрами узлов в конструкции. Как показали исследования влияния деформативности соединений в разрезных и неразрезных пролетных строениях увеличение усилий происходит с ростом деформативности узлов.
В работах [1, 2] приводится методика учета податливости стыков на несущих высокопрочных болтах при расчете балочных пролетных строений. Авторы в своих исследованиях приходят к выводу о нелинейной зависимости между углом раскрытия упругого шарнира и изгибающим моментом.
Вышеизложенные обзор научно-исследовательских работ в области решетчатых каркасных конструкциях свидетельствует о существенном влиянии деформативности болтовых соединений на перераспределении внутренних усилий в элементах статически неопределимых систем и на деформации системы в целом.
Столь значительное влияние смещений в соединениях вынуждает весьма внимательно подходить к проектированию и расчету инвентарных надстроек вспомогательных опор, элементы которых соединяются на болтах нормальной точности.
Вопрос влияния смещений в болтовых соединениях на работу вспомогательных стационарных и плавучих опор, представляющий большой интерес применительно к мостостроению, ранее рассматривался в работах автора [9,10,14–17] и был продолжен в работах [18–21]. Здесь смещения Δi в болтовых соединениях решетчатых надстроек стационарных опор учитываются посредством замены модулей упругости Е на модули линейной деформации Еэ элементов, определяемых через модули деформации болтовых соединений в начале Ес,1i и в конце Ес,2i i-го элемента.
Модуль деформации болтового соединения Есi при усилии Ni в i-м элементе запишется как:
,
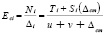где Ti – сила трения в соединении i-го элемента;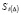 
– эмпирическая зависимость при работе соединения на смятие [8]; u – сдвиг соединения на разность номинальных диаметров болта и отверстия; v – допускаемые отклонения от номинальных диаметров болта и отверстия; Δcm – неупругая деформация смятия.
Изменение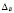 
расстояний между центрами узлов i-го элемента определяется как сумма упругой деформации 
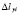и смещений в прикреплениях 
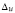и 
.
и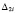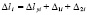ли
.
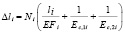Отсюда находим модель линейной деформации i-го элемента
.
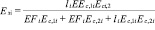Допуская, что величины смещений в соединениях в начале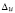 
и конце 
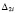i-го элемента одинаковы, модуль деформации элемента будет определять по формуле
.
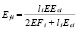Расчет ведется методом итераций с поэтапным уточнением усилий в элементах. Итерационный процесс можно выполнять также уточняя напряжения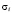 
в i-м элементе. В этом случае формула для определения модуля деформации будет иметь вид
.
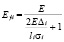В первом приближении значения Eэi определяются по напряжениям в конструкции с несмещающимися узлами.
Сдвиги в болтовых соединениях понтонов учитываются посредством введения упругих шарниров с коэффициентами жесткости Ki. Значения коэффициентов жесткости определяются по формуле:
,
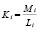где Mi – момент в i-м шарнире; Li – угол раскрытия i-го шарнира.
С учетом вышеприведенных результатов научно-исследовательских работ определены задачи дальнейших исследований по выявлению напряженно-деформируемого состояния стационарных и плавучих вспомогательных опор для строительства мостов с учетом смещений в болтовых соединениях, деформаций фундаментов и взаимодействия, при совместной работе, надстроек с плашкоутами плавучих опор.
С учетом результатов исследований предложен метод расчёта вспомогательных стационарных и плавучих опор с учетом смещений в болтовых соединениях надстроек и плашкоутов. Основу расчета составляет замена модулей упругости материала на модули деформаций элементов решетчатых конструкций, а также введение упругих шарниров в местах болтовых соединений плашкоутов плавучих опор. Предложенная методика расчета плавучих опор распространяется на случаи как узких, так и широких плашкоутов. В результате численного анализа установлено, что наибольшее влияние смещения в соединениях оказывают на элементы решетки.
Библиографическая ссылка
Должиков В.Н. ВЛИЯНИЕ ПОДАТЛИВОСТИ БОЛТОВЫХ СОЕДИНЕНИЙ НА РАБОТУ ВСПОМОГАТЕЛЬНЫХ ОПОР ДЛЯ СТРОИТЕЛЬСТВА МОСТОВ. ОБЗОР // Международный журнал экспериментального образования. – 2016. – № 11-2. – С. 243-248;URL: https://expeducation.ru/ru/article/view?id=10871 (дата обращения: 19.04.2024).