В Новосибирском государственном техническом университете (НГТУ) на кафедре Аэрогидродинамики (АГД) в аэродинамической трубе дозвуковых скоростей Т-503 широко проводятся экспериментальные исследования в области дозвуковой аэродинамики, в частности, изучаются вопросы возникновения и развития нестационарных отрывных процессов в воздушном потоке.
Исследования нестационарных отрывных течений имеют важное фундаментальное и прикладное значение, так как позволяют выявить причины возникновения аэроупругих колебаний элементов различных механических конструкций, которые нередко могут приводить к разрушению промышленных сооружений (мостов, зданий и т.п.).
Для обеспечения эффективной работы аэродинамической трубы силами сотрудников кафедры АГД НГТУ и специалистов Института теоретической и прикладной механики (ИТПМ) СО РАН в настоящее время за счет средств РФФИ создается система управления и сбора экспериментальных данных представляемой аэродинамической установки [1].
Важной задачей при проведении экспериментальных исследований является обеспечение постоянства скорости потока воздуха в аэродинамической трубе [2].
Данная работа посвящена описанию методики и алгоритмов, обеспечивающих решение представленной задачи [3].
Автоматическое регулирование и поддержание скорости потока в аэродинамической трубе.
Регулирование скорости потока и поддержание ее в заданных пределах в аэродинамической трубе Т-503 построено по классическому принципу ПИД-регулятора. Типы и свойства таких регуляторов описаны в [4].
Поток воздуха в аэродинамической трубе обеспечивается вентилятором с электрическим приводом мощностью до 250 кВт. Электрический привод управляется постоянным током от регулируемого выпрямителя. Управляющее напряжение на входе выпрямителя имеет диапазон 0…5 вольт. При подаче на управляющий вход указанного напряжения, выходное напряжение выпрямителя меняется от 0 до максимального значения в 400 вольт, что обеспечивает обороты двигателя, создающие скорость потока за вентилятором в диапазоне 5…60 м/с.
Значение скорости потока вычисляется по разности полного и статического давлений, измеренных с помощью датчика давления.
Таким образом, имеем классическую схему автоматизированной системы управления (АСУ), состоящую из исполнительного механизма (двигателя), регулятора (ПЭВМ и выпрямителя ) и цепи обратной связи (датчика давления). Применительно к нашему случаю, воспользуемся описанием и методикой настройки регулятора, изложенной в [5].
Прибавка управляющего воздействия в цифровом регуляторе вычисляется по формуле:
,
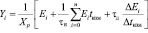где Xp – полоса пропорциональности; Ei – рассогласование или разность между уставкой Tуст и текущим значением измеренной величины Ti; tд – дифференциальная постоянная;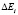 
– разность между двумя соседними рассогласованиями Ei и Ei-1; Δtизм – время между двумя соседними измерениями Ti и Ti-1; τи – интегральная постоянная; 
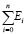– накопленная в i-й момент времени сумма рассогласований (интегральная сумма).
Выходное напряжение ЦАП, суммируя воздействия, вычисляется по формуле:
.
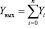Из-за отсутствия точных параметров привода (масса, моменты, характеристики рабочего колеса и т.д.) параметры ПИД-регулятора целесообразно подбирать опытным путем.
Есть очень важный момент при разработке ПИД-регулятора: воздействие должно быть строго периодичным, т. е. производиться через равные промежутки времени.
Аналогично, рассогласование и воздействие должны вычисляться также периодически. Для успешной работы алгоритма важно выбрать период опроса датчика и выработки величины воздействия. Из опытных пусков необходимо оценить постоянную времени привода (τп). Период опроса датчика разумно взять в диапазоне от τп/5 до τп/10. Постоянная времени оценивается при подаче на управляющий вход ступеньки, примерно половинного диапазона и записи величины скорости набегающего потока (по датчику давления) в реальном времени. По графику и определяется постоянная времени.
Далее, опытным путем, последовательно подбираются величины Хр, τи, τд, начиная с минимальных значений. При подборе снимаются диаграммы и оценивается необходимость изменения параметра в ту или иную сторону. На управляющий вход выпрямителя подается ступенька и отслеживается процесс установления нового режима. Пользуясь методикой, предложенной в [5], производится коррекция коэффициентов. В дальнейшем, эти коэффициенты используются в управляющей программе ПИД-регулятора.. В процессе подбора коэффициентов, вполне возможно, необходимость применения всего набора коэффициентов (τи, τд) может и не потребоваться.
Заключение. Таким образом, в данной работе представлено описание алгоритмов и методов, с помощью которых обеспечивается управление и поддержание постоянства скорости потока в рабочей части аэродинамической трубы.
В настоящее время эти алгоритмы используются в опытном варианте системы управления представляемой аэродинамической трубы.
Данная работа выполнялась при финансовой поддержке грантов РФФИ № 14–07–00421 и 12–07–00548.
Авторы выражают искреннюю благодарность старшему лаборанту кафедры Аэрогидродинамики НГТУ Слободскому И.В. за помощь в выполнении работы.
Библиографическая ссылка
Башуров В.В., Гилев В.М., Саленко С.Д., Шпак С.И. АВТОМАТИЧЕСКОЕ РЕГУЛИРОВАНИЕ И ПОДДЕРЖАНИЕ СКОРОСТИ ПОТОКА В АЭРОДИНАМИЧЕСКОЙ ТРУБЕ // Международный журнал экспериментального образования. – 2016. – № 11-2. – С. 263-264;URL: https://expeducation.ru/ru/article/view?id=10885 (дата обращения: 22.12.2024).