Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Глущенко А.Г. 1 Глущенко Е.П. 1 Устинова Е.С. 2

---

1 ФГБОУ ВО «Поволжский государственный университет телекоммуникаций и информатики»

2 ФГБОУ ВО «Поволжский государственный университет сервиса»

Рассмотрены особенности интерференции волн, формируемых точечными когерентными источниками в движущихся однородных, изотропных средах. Показано, что движение среды существенно меняет интерференционную картину, формирует асимметрию интерференционной картины в направлении движения среды, что необходимо учитывать при расчете распределения направления излучения системы излучателей. Если скорость движения среды растет, то увеличивается сдвиг интерференционной картины. Получены соотношения для аналитического расчета амплитуды и фазы результирующих колебаний с учетом движения среды. Соотношения, полученные в работе, могут быть использованы для расчета распределения интенсивности и фазы результирующего колебания в любой точке пространства при любом пространственном расположении источников и при произвольном направлении и скорости движения среды. В работе приведены результаты расчета изменения интерференционной картины четырех источников излучения при увеличении скорости движения среды.

Статья в формате PDF

0 KB

интерференция

движение среды

1. Гринченко В.Т., Вовк И.В., Мацыпура В.Т. Основы акустики. – Киiв: Наукова думка, 2007. – 640 с.

2. Осташев В.Е. Распространение звука в движущихся средах.– М.: Наука, 1992. – 208 с.

3. Шкундин С.З., Румянцева В.А. Повышение точности измерения скорости воздушного потока акустическим анемометром // Измерительная техника – 2001. – №1. – C. 54–57. 

4. Глущенко А.Г., Глущенко Е.П., Устинова Е.С. Невзаимные волновые процессы // European research. – 2015. – № 10 (11).– C. 9.

5. Глущенко А.Г., Глущенко Е.П. Методика расчета пространственного распределения интенсивности волнового процесса, формируемого точечными источниками// Вестник науки и образования. – 2016. – №11(23). – C. 6–9.

Излучение разнесенных в пространстве когерентных источников сопровождается формированием интерференционной картины стационарного перераспределения интенсивности для волновых процессов любой физической природы. Расчет пространственного распределения интенсивности является классической задачей излучения акустических и электромагнитных источников и проводится в аналитическом виде обычно для двух источников в изотропных средах [1–3], и численно для более сложных конфигураций. Движение среды может существенно влиять на волновые процессы, что наиболее наглядно проявляется для акустических волн [3], поскольку скорость движения среды может быть сопоставима со скоростью распространения волн в этих средах [4–5]. Методика аналитического расчета интерференционной картины от произвольного числа источников была рассмотрена в работе [4].

Основные соотношения. Рассмотрим здесь влияние движения среды на интерференционную картину, создаваемую когерентными источниками волн 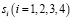(рис. 1) в акустической среде, характеризуемой скоростью распространения волн 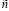. Среда движется в общем случае со скоростью u под углом к оси 0y.

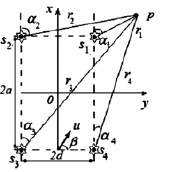
Рис. 1. Сложение волн от четырех источников в подвижной среде

В соответствии с принципом суперпозиции суммарное давление поля в любой точке пространства P определяется суммой давлений, создаваемых каждым источником:

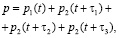
где 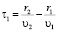, , 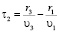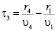– это время задержки волн, проходящих пути 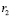от второго, 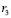третьего и 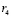четвертого источников по сравнению с расстоянием, проходимом волной, распространяющейся по пути 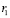от первого источника излучения. Скорости распространения для всех четырех волн от источников в направлении точки наблюдения P в общем случае различаются и определяются направлением скорости движения среды u:

, , , .

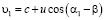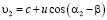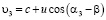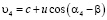Различаются, следовательно, и волновые числа всех четырех волн:

.

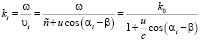Углы 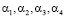направлений распространения каждой из волн от источников в точку наблюдения P, определяются соотношениями (рис. 1):

,

,

,

,

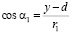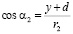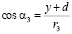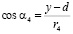где расстояния от источников до точки наблюдения:

,

.

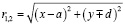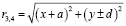При наложении когерентных волн в точке P возникает результирующая волна с той же частотой и амплитудой волны определяемой соотношением:

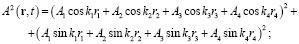
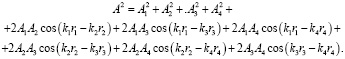
Фаза результирующего колебания определяется в виде:

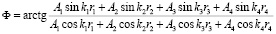
Интенсивность волнового процесса в точке P может быть представлена в виде:

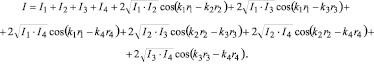
Максимальная интенсивность

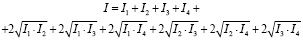
будет наблюдаться в тех точках, для которых одновременно выполняются соотношения 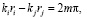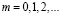. При равной интенсивности всех источников 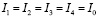имеем соотношение:

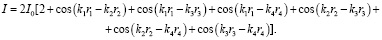
Отметим, что полученные соотношения могут быть использованы для расчета распределения интенсивности и фазы результирующего колебания в любой точке пространства при любом пространственном расположении источников. На рис. 2 показано влияние скорости движения среды (при 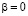) на распределение интенсивности интерференционной картины, создаваемой источниками, расположенными в вершинах прямоугольника (рис. 1).

Рис. 2. Пространственная зависимость распределения интенсивности от относительной скорости движения среды

Выводы

Движение среды формирует асимметрию интерференционной картины отдельных источников (различимых на картине распределения интенсивности до скорости движения среды 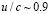) в направлении движения среды. С ростом скорости движения среды растет «снос» интерференционной картины. Таким образом, движение среды существенно меняет интерференционную картину, что необходимо учитывать при расчете диаграммы направленности системы излучателей.

Библиографическая ссылка