Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Файлы
• Литература

Когай Г.Д. 1 Тен Т.Л. 1 Абилкаир А.Н. 1

---

1 Карагандинский экономический университет Казпотребсоюза

Статья в формате PDF

0 KB

1. Ковалев В.В. Анализ финансового состояния и прогнозирование банкротства. – СПб.: Аудит Ажур, 1994. – 163 с.

2. Ч ерныш Е.А. Прогнозирование и планирование в условиях рынка: Учеб. пособие / Е.А. Ч ерныш, Н.П. Молчанова, А.А. Новикова, Т.А. Салтанова. – М.: ПРИОР, 1999. – 176 с.

3. Piech K . K nowledge and innovation processes in C entral and E ast E uropean economies, W arsav, 2007, p.34.

4. C ruz, I nes; S capens, R obert W .; Major, Maria (2011): The localisation of a global management control system. I n Accounting, O rganizations and S ociety 36 (7), pp. 412–427.

Несомненная важность и недостаточная изученность многоаспектных проблем анализа и многофакторных методов прогнозирования финансового состояния, необходимость формирования прогнозно-аналитической системы, позволяющей получать реальную и потенциальную оценку эффективности деятельности коммерческих организаций, и установление ее составных компонентов, определяют актуальность данных исследований.

Прогнозирование финансовой устойчивости коммерческого предприятия представляет собой совокупность аналитических процедур, применяемых для диагностики финансовой устойчивости хозяйствующего субъекта в перспективе при помощи разработанных методик анализа и прогнозирования финансовой устойчивости на основе действующих методов и приемов экономического анализа и прогнозирования.

При изучении закономерностей экономических явлений большое значение имеет выявление связей между взаимосвязанными, развивающимися явлениями во времени, проведение анализа динамики. С этой же целью строятся модели множества факторов, взаимосвязанных временным рядом.

Факторный анализ – это методика комплексного и системного изучения и измерения факторного воздействия на величину показателей, влияющих на результат [1].

Многофакторная модель – это модель, построенная по нескольким временным рядам, значении коих относятся к одинаковым временным отрезкам или же датам. Моделирование связных линий динамики основано на применении уравнений регрессии. Похожие модели отражают образовавшиеся меж исследуемыми показателями связи с необходимой степенью точности и дают возможность расценить уровень воздействия отдельных моментов на действенный симптом, а еще эффективность воздействия всех факторных признаков.

Основная часть. Для разработки модели оптимизации финансовой устойчивости в работе воспользуемся методом корреляционно-регрессионного анализа. Корреляция представляет собой возможную зависимость меж показателями, которые не находятся в функциональной зависимости. Этот метод применяется для определения тесноты взаимосвязи меж показателей финансовой устойчивости [2].

Введем такие обозначения: х1 – коэффициент автономии; х2 – коэффициент финансового риска; х3 – коэффициент долга; х4 – коэффициент финансовой устойчивости; х5 – коэффициент маневренности; х6 – коэффициент обеспеченности собственными средствами оборота.

Составляем экономическую модель множественной регрессии в таком виде:

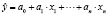
определим оценки а0, а1, …, аn параметров по методу наименьших квадратов (МНК).

Коэффициенты аi – иллюстрируют, на сколько измениться результативный показатель при смене факторного на единицу [3].

Нужные исходные данные берутся из табл. 1 и рассчитываются параметры уравнения регрессии.

Таблица 1

Параметры уравнения регрессии

* Таблица составлена автором на основе расчета.

Составляем экономическую модель по данным табл. 1 и получаем систему многофакторных моделей формирующих показатель коэффициента финансовой устойчивости:

.

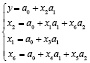Таким образом, решается задача максимизации показателя y при указанных ограничениях.

Оценки а0, а1, а2 рассчитываются по МНК:

Уравнение регрессии с оценками параметров выглядят так:

.

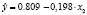Совместный коэффициент многочисленой корреляции ry характеризует тесноту связи результативного y и факторных х1, х2, …, хm признаков и в определяется по формуле:

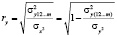, (1)

где 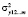– факторная дисперсия; 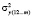– остаточная дисперсия; 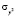– дисперсия результативного признака:

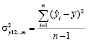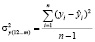; ; (2)

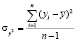, (3)

где 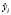– расчетное значение результативного признака; 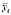– среднее значение результативного признака.

Приведенную форму записи индексов можно трактовать таким образом:

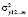– дисперсия 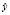, полученная с учетом факторов х1, х2, … , хm ; 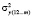– дисперсия y, полученная с учетом факторов х1, …, хm;

Чем плотнее фактические значения yi располагаются в сравнении с линией регрессии, тем меньше остаточная дисперсия и больше факторная дисперсия и больше величина ry.

Так, коэффициент множественной корреляции охарактеризовывает качество подбора уравнения регрессии, как и величина остаточной дисперсии.

Квадрат величины ry – коэффициент множественной детерминации, характеризует долю воздействия выбранных признаков на результативный фактор:

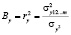(4)

По данным сквозного примера имеем:

; ;

; ; .

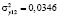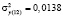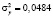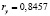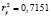В соответствии с таблицей Чеддока, взаимосвязь результативных признаков считается высокой (0,71). Регрессия у на х1 на 71 % объясняет изменение показателя: Коэффициент долга.

Значение коэффициентов находится в пределах 0 ry 1 .

В отсутствие взаимосвязи меж результативными и факторными признаками факторная дисперсия приравнивается нулю, коэффициент множественной корреляции приравнивается нулю и линия регрессии совпадает с прямой 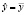. При функциональной взаимосвязи факторная дисперсия совпадает с общей дисперсией, а коэффициент корреляции приравнивается 1.

Оценка значимости коэффициента детерминации определяется с использованием критерия Фишера. По данным расчетов критерий Фишера имеет следующий вид:

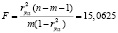. (5)

По таблице F-распределения находим для степеней свободы f1= m = 2 и f2= n – m – 1 = =7 – 2 – 1 = 4, a = 5 %, Fкр = 5,32, и значение коэффициента детерминации и значение коэффициента множественной корреляции считаются значимыми (F>Fкр).

Для оценки вклада во множественный коэффициент корреляции каждого из факторов используют частные коэффициенты корреляции.

Частный коэффициент корреляции – показатель, характеризующий тесноту взаимосвязи меж признаками при элиминации всех остальных. В общем случае формула для нахождения частного коэффициента корреляции между факторами у и х при элиминации влияния факторов х1, …, хm-1 имеет вид

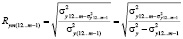, (6)

где 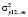– факторная дисперсия регрессии у на х1, х2, … , хm; 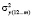– факторная дисперсия у, полученная с учетом факторов х1, …, хm-1; 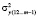– остаточная дисперсия регрессии у, полученная с учетом факторов х1, х2, …, х; 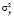– дисперсия результативного фактора.

Величина частного коэффициента корреляции находится в пределах от 0 до 1, а знак определяется знаком соответствующих параметров регрессии.

Принимая вместо s2 его оценку S2:

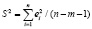, (7)

где n – число наблюдений; m – число объясняющих переменных.

Тогда

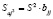, (8)

где bjj – диагональные элементы матрицы оценки параметров уравнения регрессии.

Квадратическая ошибка 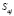равна:

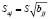. (9)

Учитывая, что

,

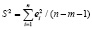имеем:

S = 0,4625;

Sa0 = 0,0998;

Sa1 = 0,0511.

Расчетный критерий ti равен

; .

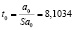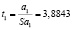Для доверительной вероятности р=0,95 и числа степеней свободы k=8 по таблице Стьюдента находим tкр = 2,57. По этому критерию в уравнении регрессии значимыми являются все параметры: а0, а1, а2 [4].

t0 = 8,1034>tкр = 2,57;

t1 = 3,8834>tкр = 2,57.

Для остальных финансовых показателей экономической модели разработан ряд многофакторных моделей и получены расчетные характеристики этих уравнений.

Таблица 2

Прогнозные значения коэффициента финансовой устойчивости на период 2013–2016 гг.

* Таблица составлена автором на основе расчета.

Таблица 3

Прогнозные значения коэффициента долга на период 2013–2016 гг.

* Таблица составлена автором на основе расчета.

Таблица 4

Прогнозные значения коэффициента финансового риска (коэф. задолженности, соотношения заемных и собственных средств, рычага)на период 2013–2016 гг.

* Таблица составлена автором на основе расчета.

Таблица 5

Прогнозные значения коэффициента обеспеченности оборотного капитала собственными источниками финансирования на период 2013–2016 гг.

* Таблица составлена автором на основе расчета.

Уравнение Y = 0.809 – 0.198 X2 свидетельствует о снижении коэффициента финансовой устойчивости на 0,198 единиц ( далее – ед.) в случае повышения X2 – коэффициента долга на 1,0 ед. Уравнение X2 = 1.760 – 2.154 X1 + 5.584 X6 также свидетельствует о том, что коэффициент долга меняет свое значение на 1,0 ед под воздействием изменения параметров коэффициента финансового риска на 2,154 ед. и коэффициента обеспеченности оборотного капитала собственными источниками финансирования на 5,584 ед.

В случае снижения коэффициента автономии на 1,0 ед., в соответствии с уравнением X1 = 0.556 – 0.204 X3 происходит снижение коэффициента финансового риска на 0,204 ед.

Уравнение X6 = – 0.270 – 0.637 X4 + 2.323 X5 показывает зависимость коэффициента обеспеченности оборотного капитала собственными источниками финансирования от коэффициента маневренности собственных средств на 0,637 ед. и коэффициента устойчивости структуры мобильных средств на 2,323 ед.

Выводы

Так, прогнозные значения, полученные по системе многофакторных регрессионных уравнений, могут служить основой для индикации планирования финансовой стратегии развития организации на последующие годы. Отклонения вполне допустимые, если учитывать структуру исходных статистических рядов.

При стремлении максимизировать значение коэффициента финансовой устойчивости, полученные прогнозные сведения свидетельствуют, что у организации коэффициент финансового риска и долга должен быть приближен или равняться нулю. Коэффициент маневренности при этом имеет направленность к снижению, что говорит о не гибком применении собственных источников. Данные решения вполне реализуемы и применимы на практике, в случае привлечения заемных средств для нормальной функциональности организации.

Библиографическая ссылка