Федеральные государственные образовательные стандарты основного общего образования (ФГОС ОО) ориентируют не только на предметные, но и на метапредметные и личностные результаты, тем самым они задают принципиально новую форму описания образовательных достижений школьников.
Предметные результаты образовательной деятельности обучающихся включают освоенные обучающимися в ходе изучения учебного предмета умения, специфические для данной предметной области; виды деятельности по получению нового знания в рамках учебного предмета; его преобразованию и применению в учебных, учебно-проектных и социально-проектных ситуациях; формирование научного типа мышления, научных представлений о ключевых теориях, типах и видах отношений; владение научной терминологией, ключевыми понятиями, методами и приемами [14].
Метапредметные результаты обучающихся включают освоенные обучающимися межпредметных понятий и универсальных учебных действий (УУД), способность их в учебной, познавательной и социальной практике, самостоятельность, планирование и осуществление учебной деятельности и организации учебного сотрудничества с педагогами и сверстниками, построение индивидуальной образовательной траектории [14].
Другими словами метапредметные результаты это освоенные обучающимися на базе одного, нескольких или всех учебных предметов способы деятельности, применимые как в рамках образовательного процесса, так и при решении проблем в реальных жизненных ситуациях.
Личностные результаты образовательной деятельности включают готовность и способность обучающихся к саморазвитию и личностному самоопределению; сформированность их мотивации к обучению и целенаправленной образовательной деятельности; системы значимых социальных и межличностных отношений, ценностно-смысловых установок, отражающих личностные и гражданские позиции в деятельности; социальные компетенции, правосознание; способность ставить цели и строить жизненные планы; способность к осознанию российской идентичности в поликультурном социуме [14].
Метапредметные результаты, согласно ФГОС ОО, включают УУД и межпредметные понятия. УУД в свою очередь включают четыре группы действий: личностные, познавательные, регулятивные и коммуникативные.
В группе познавательных УУД выделяют логические, общеучебные, знако-символические и моделирование.
Формирование указанных компонентов базируется на логических операциях: анализ, синтез, сравнение, выделение свойств понятия, определение понятия, подведение под понятие, обоснование, классификация, обобщение и др.
Эти логические операции, как показывает практика, целесообразно, в первую очередь, формировать в учебном предмете «Математика», который предоставляет для этого широкие возможности: устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и делать выводы; самостоятельно выбирать основания и критерии для классификации и т. д.
Математика, как никакой другой предмет, позволяет формировать у учащихся умения подмечать закономерности, умение пользоваться контрпримерами, умение выводить следствия из заданных условий, умение приводить доказательные рассуждения, делать выводы; знакомить учащихся с понятиями простых и сложных высказываний и значениями их истинности; знакомить с понятием отрицания высказываний и с понятием противоречивых высказываний и т.д.
В наших работах [3, 4] ведется обстоятельный разговор о содержании и методических особенностях такой работы, в этой же статье мы остановимся лишь на основных аспектах такой работы при чем сделаем акцент на работе в 5–6 классах.
1. Ознакомление учащихся с простыми и сложными высказываниями и значениями их истинности
Любое математическое предложение является либо элементарным, не расчленяющимся на части, каждая из которых, в свою очередь, есть предложение, либо сложным, построенным из элементарных. Так, например, предложение «а больше b» – элементарное, а предложение «а больше или равно b» – составное, состоящее из двух элементарных: «а больше b», «а равно b», которые соединены логическим союзом «или».
Логической структурой сложного предложения называется совокупность и порядок логических связок («не», «и», «или», «если..., то», «тогда и только тогда», «для всякого», «существует» и т.д.), с помощью которых это предложение образовано из элементарных.
Одна из задач формирования у учащихся умения доказывать теоремы, состоит в обучении их умению раскрывать логическую структуру математических предложений и устанавливать истинностные значения этих предложений.
Раскрыть логическую структуру сложного предложения, значит показать, из каких элементарных предложений сконструировано данное сложное предложение и как оно составлено из них с помощью логических связок.
Напомним, что означают некоторые логические связки (логические операции) в математической речи.
Определение 1. Отрицанием высказывания А называется высказывание, обозначаемое 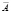 (или А), которое истинно тогда и только тогда, когда А ложно.
(или А), которое истинно тогда и только тогда, когда А ложно.
Запись 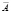 (или А) читается «не А».
(или А) читается «не А».
Определение 2. Конъюнкцией высказываний А и В называется высказывание, обозначаемое А - В (или А & В), которое истинно тогда и только тогда, когда А и В истинны.
Запись А - В (или А & В) читается «А и В».
Замечание. В математике для записи конъюнкции «в столбик» используется фигурная скобка:
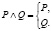
Например, при решении неравенства
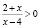 ,
,
мы должны записать такие конъюнкции 2 + х > 0 и х – 4 > 0; 2 + х < 0 и х – 4 < 0. Это может быть записано так:
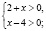
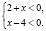
Определение 3. Дизъюнкцией высказываний А и В называется высказывание, обозначаемое А - В, которое ложно тогда и только тогда, когда истинно хотя бы одно из высказываний А, В.
Запись А - В читается «А или В».
Замечание. В математике для записи дизъюнкции «в столбик» используется квадратная скобка:
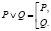
Например, при решении неравенства х2 ≥16, его решение представляет собой дизъюнкцию двух высказываний: х ≤ –4 или х ≥4. Эта дизъюнкция может быть записана так:
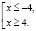
Определение 4. Импликацией высказываний А и В называется высказывание, обозначаемое А > В, которое ложно тогда и только тогда, когда А – истинно, В – ложно.
Запись А > В читается «если А то В» или «А влечет В».
Определение 5. Эквиваленцией высказываний А и В называется высказывание, обозначаемое А - В, которое истинно тогда и только тогда, когда высказывания А и В имеют одинаковые истинностные значения.
Запись А - В читается «А эквивалентно В» или «А тогда и только тогда, когда В», или «для того чтобы А, необходимо и достаточно, чтобы В».
Для разбора различных логических структур учащимся можно предложить такие сложные предложения:
а) если число целое и положительное, то оно натуральное;
б) если четырехугольник – ромб, и все его углы прямые, то четырехугольник – квадрат;
в) прямые на плоскости могут либо пересекаться, либо не пересекаться;
Для определения истинностных значений можно предложить школьникам такие высказывания (заметим, что сложность этого задания может быть по желанию учителя понижена):
а) Если 12 делится на 6, то 12 делится на 3.
б) Если 11 делится на 6, то 11 делится на 3.
в) Если 15 делится на 6, то 15 делится на 3.
Операцию расчленения сложных высказываний на простые можно отработать с учащимися на таких предложениях:
а) Если летом мы поедем в Омск и у нас будет достаточно времени, то мы посетим драматический театр.
б) Если летом будет дождливая погода, то ни накупаться нам не удастся, ни загореть нам не удастся.
в) Если мы скоро окончим работу и будет хорошая погода, то мы пойдем на прогулку или поедем на пляж.
2. Ознакомление школьников с понятием отрицания высказываний и с понятием противоречивых высказываний
Ознакомить учащихся на интуитивном уровне с понятием отрицания высказываний и с понятием противоречивых высказываний, это значит помочь им усвоить в дальнейшем метод доказательства от противного, который широко применяется в школьных учебниках геометрии.
Уже на уровне 5–6 классов учащимся можно предлагать задания, при выполнении которых школьники строят свои рассуждения методом от противного. Так, например, можно поступить при выполнении такого задания: «Число р не делится на 2. Докажите, что число р не длится на 4». Рассуждения могут быть такие: «Если бы число р делилось на 4, то тогда существовало бы такое число х, что р = 4х. Отсюда р = 2(2х), то есть число р делилось бы на 2, но это противоречит условию. Следовательно, р не делится на 4».
Приведем примеры, посредством которых можно формировать у учащихся умения строить отрицания высказываний и обнаруживать противоречивые высказывания.
1) Выяснить, могут ли быть одновременно верными и неверными следующие высказывания:
а) а больше b; а меньше b;
б) а больше b; произведение чисел а и b равно 0;
в) 2 +3 = 5; 2 + 3 1 5;
2) Существуют ли два таких числа а и b, для которых выполняются два таких свойства:
а) 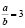 ; аb = 0;
; аb = 0;
б) 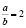 ; аb = 2;
; аb = 2;
3) Найдите такие два натуральных числа m и n, для которых выполняются три свойства: mn = 0; m меньше n на 2; m + n = 2.
4) Укажите, какие из высказываний, в предложенных ниже парах, являются отрицанием друг друга:
а) 5 > 0 и 5 ≤ 0;
б) 3 + 7 = 10 и 3 + 7 < 10;
в) а ^ b и а || b;
5) Составьте отрицания следующих высказываний:
а) весь наш класс присутствовал на вечере самодеятельности;
б) некоторые школьники по контрольной работе получили пять;
в) ни один из сомножителей произведения аbс не равен 0;
6) Среди следующих утверждений найдите пары высказываний, являющихся отрицанием друг друга:
а) все ученики нашего класса решили задачу;
б) некоторые ученики нашего класса не решили задачу;
в) некоторые ученики нашего класса решили задачу;
7) Отрицаниями каких предложений являются высказывания:
а) в каждом городе есть район, в каждой школе которого найдется класс, ни один ученик которого не занимается спортом;
б) найдется книга, содержащая страницу, в каждой строке которой встречается хотя бы одна буква «а».
3. Обучение учащихся умению пользоваться контрпримерами
Учить школьников приводить примеры, иллюстрирующие или доказывающие высказывания, либо контрпримеры, опровергающие предложения, значит учить их творческому подходу к изучению математики. Такая работа исключает шаблонность в действиях учащихся и позволяет преодолеть формализм в знаниях.
В школьной практике чаще всего предлагаются задания, в которых учащимся следует доказать то или иное утверждение и это приводит к тому, что они становятся беспомощными, испытывают робость перед заданиями типа: «Проведите доказательство или опровержение какого-либо утверждения».
Учителю следует показать школьникам уже V-VI классов, что примеры доказывают частноутвердительные и частноотрицательные предложения, а контрпримеры опровергают предложения общего характера.
В математике наиболее употребительны следующие четыре логических формулы:
1) 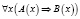 ; 3)
; 3) 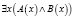 ;
;
2) 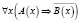 ; 4)
; 4) 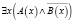 .
.
Суждения 1) и 2) опровергаются контрпримерами, а суждения 3) и 4) – доказываются примерами.
Мы, следуя Н.А. Курдюмовой [7], будем трактовать понятия «пример» и «контрпример» следующим образом: если для некоторой логической формулы F, имеющей предметную область D, в этой области D существует такое распределение значений параметров, входящих в формулу F, при котором F принимает значение «истинно» («ложно»), то такое распределение называется выполняющим (опровергающим) распределением для F в D, или примером (контрпримером).
Контрпримеры чаще всего применяются тогда, когда надо убедить учащихся в том, что они ошибаются. Чтобы убедиться в ложности некоторого общего высказывания, достаточно привести один контрпример.
Вообще следует заметить, что школьники часто считают, что из суждения «Всякое К есть Р» следует «Все Р суть К», вместо частно-утвердительного «Некоторые Р суть К».
Учащимся на уровне V-VI классов может быть предложено задание: Приведите контрпримеры, доказывающие ложность следующих высказываний:
а) любое число, оканчивающееся единицей, делится на 3;
б) любая фигура, имеющая три угла, является треугольником;
в) любые три отрезка могут быть сторонами треугольника;
Формировать у учащихся умение приводить примеры помогут такие задачи:
а) подберите такие значения х и у, для которых верно равенство 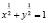 ; как вы думаете, сколько можно подобрать таких пар значений х и у?;
; как вы думаете, сколько можно подобрать таких пар значений х и у?;
б) укажите значения l, чтобы вектор 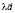 был бы противоположно направлен вектору
был бы противоположно направлен вектору 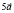 ;
;
в) график функции у = ах2 + bх + с пересекает прямую у = 2 в двух точках, а прямую у = 1 – в одной точке; приведите примеры возможных значений а, b, с.
4. Формирование у учащихся умения выводить следствия из заданных условий
А.А. Столяр [13] в обучении учащихся доказательствам выделяет два основных уровня:
а) первый уровень (5–8 классы) – используемые в доказательствах правила вывода остаются невыясненными, они применяются в неявном виде, основное внимание уделяется выяснению того, «что следует» и «из чего следует», но не «как это следует»;
б) второй уровень (9–11 классы) – понятие доказательства может быть несколько уточнено, если учащимся разъясняются простейшие правила вывода и им становится доступным анализ доказательства, выявление его логической структуры, используемых в нем правил вывода, то есть уделяется внимание и тому «как это следует».
В данной работе мы остановимся на первом уровне. Приведем примеры, на которых возможно формировать у учащихся умение выводить следствия из заданных условий.
1) Известно, что АВ – отрезок. Сделайте из этого выводы.
Ответ: АВ – часть прямой; точки А и В – концы отрезка; все другие точки отрезка лежат между точками А и В.
2) Известно, что ВС – биссектриса угла АВD. Сделайте из этого выводы.
3) Что можно сказать о наибольшем общем делителе нескольких чисел, если каждое из данных чисел умножить на одно и то же число?
Ответ: наибольший делитель этих чисел умножится на то же самое число.
4) Если некоторое число является общим делителем данных чисел, то чем оно является по отношению к их наибольшему общему делителю?
Ответ: всякий общий делитель данных чисел есть делитель их наибольшего делителя.
5. Формирование у учащихся умения проводить доказательные рассуждения, делать выводы
Умения проводить доказательные рассуждения входят в число основных интеллектуальных умений. Ведущая роль в формировании этих умений принадлежит геометрии, однако, как показал анализ школьной практики, успех в этой работе в значительной степени предопределен готовностью учащихся уже в начале курса выполнять различные виды деятельности, связанные с проведением доказательных рассуждений. Готовить школьников к проведению доказательных рассуждений следует уже в курсе математики V-VI классов, но эту работу следует проводить и в VII-IX классах.
Следуя А.Н. Капиносову [6], мы под рассуждениями (проведением рассуждений) понимаем мыслительную деятельность, направленную на решение определенных задач, состоящую из актуализации некоторых ранее известных субъекту суждений и выполняемых на их основе переходов от одних суждений к другим. Под доказательными рассуждениями понимаются такие, в которых основаниями перехода от одних суждений к другим являются теоретические предложения (аксиомы, теоремы, определения некоторой математической теории).
В методической литературе выделяют четыре уровня проведения доказательных рассуждений:
– простого воспроизведения (предъявленная задача распознается субъектом как ранее решенная и рассуждение представляет воспроизведение известного);
– обобщенного воспроизведения (рассуждение проводится на основе выделения общего в условии и требовании предъявленной задачи и ранее решенной или на основе распознавания задачи как принадлежащей к типу задач с известной схемой рассуждения);
– логического поиска (решение задачи отыскивается на основе выполнения действий выведения следствий и отыскания достаточных условий);
– логико-эвристический (выполнение действий выведения следствий или отыскания достаточных условий связано с применением различного рода эвристик).
Первые два уровня являются репродуктивными, а последние два – продуктивные. На уровне V-VI классов учащихся надо учить проводить доказательные рассуждения на первых трех уровнях, четвертый уровень относится к более поздним ступеням обучения. Обучать учащихся умениям доказательно рассуждать в V-VI классах надо в основном на числовом материале, ибо он занимает в этом курсе значительный удельный вес и он логически относительно прост. В свое время А.И. Маркушевич отмечал: «Логическая структура арифметических и алгебраических вопросов и задач, как правило, является простой, отчетливой, поэтому их следует в значительно большей мере, чем это делалось до сих пор, привлекать в целях математического воспитания» [8, с.40].
Приведем примеры некоторых заданий, на которых может строиться работа по формированию у учащихся умения проводить доказательные рассуждения, но прежде на двух задачах покажем, как должен строиться ответ школьников.
Задание 1. Число а – отрицательно. Положительным или отрицательным числом будет (–8 + а)? Ответ обосновать.
Ответ: Число (–8 + а) – отрицательно, так как сумма отрицательных чисел – число отрицательное.
Задание 2. Может ли значение выражения 2аb – а – 3b быть отрицательным при отрицательных значениях а и b? Ответ обосновать.
Ответ: Нет, ни при каких отрицательных значениях а и b значение указанного выражения не может быть отрицательным, так как при любых отрицательных значениях а и b каждое слагаемое выражения (2аb; –а; –3b) есть число положительное, а сумма положительных чисел всегда есть число положительное.
Как показал анализ школьной практики, умения доказательно рассуждать не приобретаются учащимися спонтанно, их нужно целенаправленно формировать и развивать посредством специально подобранных задач. М.Е. Драбкина и И.Л. Никольская отмечают: «Если ограничиться только разбором образцов доказательств в классе и решением обычных (предлагаемых учебником) задач на доказательство, то только у отдельных, лучших учащихся стихийно вырабатываются соответствующие приемы мыслительной деятельности, но они не достаточно осознаются ими как общие приемы. Большинство же учащихся беспомощны, когда им приходится самим решать задачи на доказательство» [5, с.6].
На пропедевтическом уровне школьников следует учить строить не только индуктивные, но и дедуктивные рассуждения, они-то и будут в последствии положены в основу доказательства теорем. Рассмотрим два примера дедуктивных рассуждений.
Пример 1. Докажите, что числа а = –135 и b = –207 не обращают в нуль выражение
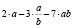 .
.
Индуктивное рассуждение основывалось бы на непосредственной подстановке указанных значений а и b в выражение (значение выражения будет отлично от нуля).
Дедуктивное обоснование того, что а = –135 и b = –207 не обращают в нуль заданное выражение, будет строиться следующим образом.
При подстановке в заданное выражение любых отрицательных значений а и b, каждое слагаемое этого выражения (2а; 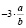 ; –7аb) будет отрицательным числом, которые в сумме не могут дать нуль. Так как числа а = –135 и b = –207 отрицательны, то и они не обращают в нуль заданное выражение.
; –7аb) будет отрицательным числом, которые в сумме не могут дать нуль. Так как числа а = –135 и b = –207 отрицательны, то и они не обращают в нуль заданное выражение.
6. Формирование у учащихся умения подмечать закономерности
Формировать у школьников умения подмечать закономерности можно на основе наблюдений, вычислений, преобразований и сопоставлений.
Д. Пойа, обращаясь к преподавателям математики, призывал: «Результат творческой работы математика – доказательное рассуждение, доказательство, но доказательство открывают с помощью правдоподобных рассуждений, с помощью догадки. ... Преподаватель должен показать, что догадки в области математики могут быть разумными, серьезными, ответственными. ... Давайте учить догадываться!».
Не будем подробно освещать этот вопрос, а ограничимся лишь примерами, на которых можно учить учащихся подмечать закономерности.
1. Продолжите числовые ряды:
а) 18, 20, 24, 32 ?
Ответ: 48
б) 212, 179, 146, 113 ?
Ответ: 80
2. Вставьте пропущенное число.
9 4 1
6 6 2
1 9 ?
Ответ: 4
3. Вставьте пропущенное число.
2 6 ? 9
54 18 81 27
Ответ: 3
4. Сравните ряды чисел:
а) 6, 10, 14, 18;
б) 5, 9, 18, 17;
в) 3, 5, 7, 9;
г) 7, 11, 15, 19;
Найдите среди них лишний ряд (ряд, не похожий на остальные ряды). Чем отличается лишний ряд от остальных?
Ответ: Ряд б) лишний.
В работе [12] выделены уровни освоения логическими УУД. Эти уровни позволяют не только проверить, как учащиеся владеют УУД, но и показывать, как они продвигаются этих универсальных учебных действий.
В основу выделенных уровней освоения логических УУД положены, выделенные в психологии, уровни сформированности способностей в зависимости от степени проявления в той или иной деятельности: репродуктивный, реконструктивный, творческий.
В этой же работе определены типы заданий по математике для каждого уровня.
Заметим, что овладеть интеллектуальными умениями, в частности, логическими приемами мышления, через воспроизводящую активность нельзя (репродуктивно-подражательная активность – самая элементарная). Это возможно сделать лишь в случае поисковой активности, при которой ученик сам включен в действия анализа, сравнения, сопоставления, классификации и т. д.
Ж.Т. Билялова, Б.Т. Абыканова, С.Б. Нугуманова отмечают: «Знания не возникают помимо познавательной деятельности субъекта и не существуют безотносительно к ней. Поэтому мы рассматриваем познавательную активность учащихся как основное условие его интеллектуального развития в целом и развития логического мышления в частности. Только в результате активного погружения самого ученика в дидактический процесс формируется интеллектуально – развитие личности» [1, с. 164].
Для диагностики сформированности логических УУД можно использовать методику А.Р. Лурия, Л.С. Цветковой.
Библиографическая ссылка
Далингер В.А. ЛОГИЧЕСКИЕ УНИВЕРСАЛЬНЫЕ УЧЕБНЫЕ ДЕЙСТВИЯ И ИХ ФОРМИРОВАНИЕ У УЧАЩИХСЯ 5–6 КЛАССОВ ПРИ ОБУЧЕНИИ МАТЕМАТИКЕ // Международный журнал экспериментального образования. 2017. № 1. С. 109-114;URL: https://expeducation.ru/ru/article/view?id=11073 (дата обращения: 15.01.2026).

