Обучение математике играет важную роль в системе средне-специальной подготовки. Математические методы в алгебре, геометрии и математическом анализе в силу своей универсальности могут быть применимы в целом на уровне научной методологии, демонстрируя связь теоретических материалов и практики. Внедрение новых стандартов в системе образования обеспечило изменение содержания программ по математике для различных сфер профессиональной подготовки и с позиции компетентностного подхода.
Во все времена обучение математике сильно влияло на формирование стиля мышления обучаемого, что является актуальным и для данного времени. Поэтому переход к новым стандартам образования, разработанным на основе компетентностного подхода, повышение эффективности обучения математике является востребованной задачей. Таким образом, компетентностный подход является основой подготовки выпускников к будущей профессиональной деятельности [2].
В обучении математике, ровно как и любой другой учебной дисциплине, для получения результатов, необходимо менять отношение к обучению, подвергнуть пересмотру содержание обучения с позиции обеспечения компетентностного подхода, осуществить внедрение инновационных технологий обучения (использование деловых игр, изменение ролей учителя и обучающихся и т.п.), использовать систему формативного оценивания, систематически повышать квалификацию учителей.
Считаем, что посредством повышения квалификации, у учителя должны формироваться следующие умения:
• Различать компетентностный и знаниевый подход к обучению, определять их особенности.
• Знать суть основных (общих) и специальных компетенций.
• Определять задачи для обучающего (учителя, преподавателя) в формировании общих и специальных компетенций у обучающихся (учеников, студентов).
• Использовать стандарты, основную образовательную программу, в планировании результатов обучения по предмету.
• Определять роль учителя в личностно-ориентированном обучении.
• Составлять дифференцированные задания в обучении.
• Планировать результаты обучения посредством использования целевых приемов личностно ориентированного обучения.
• Определять структуру и содержание уроков исходя из компетентностных задач.
Важной особенностью нового стандарта средне-специального и высшего образования является его ориентированность на формирование компетенций [1].
Под компетентностным подходом к обучению понимается обучение, целью которого является направленность на такие приоритетные векторы образования, как самоопределение, самоактуализация, социализация и индивидуальное развитие.
Обучение, которое ставит в центр формирование компетенций выпускника, таких как умение выполнять практические задачи, готовность к деятельности в профессиональной сфере, владение различными способами осуществления профессиональной деятельности и др., называется компетентностным подходом к обучению.
Вопросам внедрения и использования компетентностного подхода в Кыргызской Республике посвящены работы таких ученых, как И.Б. Бекбоева, К.М. Т?р?гелдиева, Ж.У. Байсалова, М.А. Алтыбаевой, Ш. Алиева, Э.М. Мамбетакунова, К. Турдубаевой, Д. Бабаева, С. Рысбаева, Т.М. Сияева, К.Д. Добаев и др.
Знаниевый и компетентностный подход в обучении подразумевают различные подходы в организации процесса обучения, достижения целей и обеспечения результатов. Использование этих различий требует от преподававтеля не только понимания методов и приемов, но и конретных навыков и умений.
Приводим различия между знаниевым и компетентностным подходами в обучениии (табл. 1).
Компетентностный подход выдвигает на передний план не информированность обучающегося, а способности освоения приемов решения практических и профессиональных задач.
В мировой образовательной практике компетентность выступает ключевым понятием, так как:
• объединяет в себя интеллектуальные и навыковые компоненты образования;
• компетенность стала основой развития идеологии обучения, нацеленной на результат;
• универсальные компетенции имеют интегративную природу, так как вбирают в себя ряд знаний, имеющих отношение к культурной и общепрофессиональной (информационной, правовой и т.п.) деятельности [6].
Таблица 1
|
Знаниевый подход |
Компетентностный подход |
|
Цель обучения |
|
|
Трансляция суммы, составляющих содержание образования, абстрактных ЗУН |
Ориентация на выработку результативных деятельностных приемов (методов), приоритет практики |
|
Формула результативности обучения |
|
|
(«Знаю, что …») |
(«Знаю, как …») |
|
Характер процесса обучения |
|
|
репродуктивный |
продуктивный |
|
Превалирующие компоненты процесса |
|
|
контроль |
Практика и самостоятельная работа |
|
Характер контрольных процессов |
|
|
Статистические методы оценки результатов обучения |
Комплексная оценка результатов обучения |
В государственном образовательном стандарте высшего образования Кыргызской Республики указаны следующие учебные компетенции:
– каждый фрагмент урока работает на конкретный ожидаемый результат;
– результат проводимого урока связан с долгосрочными результатами обучения, а также компетентностями, формирумыми на любом этапе урока и во внеурочное время.
Основная задача преподавателя – определение при планировании урока необходимых средств и учебных технологий в формировании компетенций, обозначенных в карте компетенций по дисциплине.
Общие требования к условиям выполнения основной образовательной программы (ООП):
• Оценка качества подготовки студентов и выпускников должна включать ежедневную (текущую), промежуточную проверку и итоговую государственную аттестацию. Проверка личных достижений студентов относительно поэтапных и конечных требований и норм (аттестация) по нормам ООП проводится посредством Базы утвержденных в нем учебных средств проверки: типовые задания, контрольные работы, тесты и другие формы проверки, нацеленные на оценку степени знаний, умений и освоенных компетенций. Базу учебных средств разрабатывает и утверждает вуз (суз) (Государственный образовательный стандарт высшего профессионального образования КР).
• Достижения учебных целей (формирование компетенций) заложенных в ООП можно проверить через фонд оценочных средств (ФОС). Оценочные средства (ОС) – фонд контрольных заданий, а также форм проверки качества освоения студентами учебных материалов, их характеристика и пояснения к использованию – являются неотъемлемой частью ООП вузов и сузов.
• Фонд оценочных средств является комплектом контрольно-методических, измерительных материалов, составленных для осуществления аттестации студентов на разных стадиях обучения, а также установления соответсвия результатов обучения требованиям государственного образовательного стандарта.
Фонд оценочных средств составляется для решения следующих образовательных задач:
• контроль и управление процессом обучения с участием всех участников процесса;
• проверка достижений целей ООП через ФОС и элементов обратной связи;
• обеспечение качества знаний, отвечающих международным стандартам образования, признание квалификаций присваиваемых в КР отечественными и зарубежными работодателями.
Требования к структуре ФОС. В ФОС должны быть включены в учебно-методическом комплексе дисциплины;
– Список формируемых компетенций при процессе освоения ООП (с указанием этапов формирования).
– Указание показателей и критериев оценки формирования компетенций на различных его этапах.
– Типовые контрольные задания для оценки деятельностных практик, ЗУНов и другие материалы хараткеризующие формирование компетенций по итогам освоения ООП.
– Методические материалы, определяющие процедуры оценки деятельностных практик, ЗУНы, характеризующие этапы формирования компетенций [4].
Здесь важно ставить достижимые, реальные цели уроков. Помимо этого, цели урока должны быть взаимосвязаны с последующими учебными материалами, а также с последующей профессиональной деятельностью студентов.
Проблема целенаправленного формирования профессиональных математических компетенций у студентов экономических сузов не может быть решена в рамках традиционных систем математической подготовки. Основным аргументом такого вывода является обострение противоречий между возрастающими требованиями к качеству образования и сокращением учебного времени. Нужны новые подходы, требующие серьезных изменений методической системы. Проблема целенаправленного формирования профессиональных математических компетенций у студентов экономических вузов не может быть решена в рамках традиционных систем математической подготовки. На практических занятиях по математике целесообразно акцентироваться на ситуационных заданиях, а разработка учебного материала должна предпологать выработку практических навыков решения математических задач.
Фундаметальная основа математической подготовки выпускника выступает основой его дальнейшей профессиоанальной жизни, так как фундаментальные знания позволят осваивать новые технологии, новые принципы и техники организации производства [3].
Навыки математического моделирования можно рассматривать как способность использовать знания на практике, значит, их можно рассматривать и как собственно формирование математических компетенций. Математическое моделирование прикладных заданий по специальности позволяют определять связь теоретических знаний студентов и их потребностей, расширять возможности использования теоретических знаний в профессиональной деятельности. Приводим некоторые примеры для экономических специальностей:
Задача. В Росинбанке установлены следующие процентные ставки:
1) 4 % от суммы вклада с ежемесячной выплатой дохода;
2) 8 % от суммы вклада при условии его хранения в течение трёх месяцев (депозит на три месяца);
3) 14,5 % от суммы вклада при условии его хранения в течение шести месяцев (депозит на полгода);
4) 18 % годовых при условии хранения вклада в течение года.
При каком условии хранения процентные деньги окажутся наибольшими, если вкладчик не будет их изымать в течение года?
Задача. Функция спроса на некоторый товар имеет вид
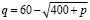 ,
,
где q – количество товара (тыс.шт.); p – цена единицы товара (сом).
Требуется найти:
1) область определения и множество значений этой функции;
2) функцию цены в виде 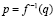 ;
;
3) объем спроса при ценах на товар: p1=500; p2=1200;
4) цену за единицу товара, если q1=20; q2=30, и выручку продавцов в каждом из этих случаев, а также построить график функции спроса
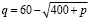 .
.
Задания прикладного характера формируют у студента необходимые для специалиста среднего звена стиль мышления, также навыки оценки полученных результатов, прогнозирования ожидаемых результатов, анализа различных ситуаций, проверки полученных результатов, оценки степени их результативности.
Таким образом, цели обучения должны определяться с тем, чтобы формировать профессиональные компетенции, а обучающие и развивающие задачи – должны быть направлены на формирование общих компетенций.
Цели обучения математике при профессиональной подготовке – получение студентом знаний, соответсвующих программе и стандартам, выработка способностей, направленных на решение типовых задач в профессиональной деятельности при помощи математических методов.
Основная цель компетентностного обучения также состоит в вышеперечисленном. Сближение содержания математической дисциплины к характеру будущей профессии посредством решения заданий и упражнений, связанных с потенциальными типовыми ситуациями и задачами производства, а также анализ таких ситуаций будет способствовать усилению мотивации студентов при обучении.
В табл. 2 приведены критерии и показатели формируемых экономико-математических компетенций у выпускников.
Таблица 2
|
Критерии |
Показатели (индикаторы) |
|
Положительная мотивация к осуществлению экономико-математической деятельности |
– Наличие заинтересованности в области экономики и математики. – Потребность в освоении компетенций в области экономики и математики |
|
Освоение теоретических и практических знаний по математике и экономике |
– Завершенный характер теоретических знаний и практических умений по математике и экономике. – Осознанность и системность знаний по математике |
|
Освоение умений по проектированию реальных фрагментов на основе методов математического моделирования |
Умение распознавать проблемы, способность переносить и применять знания в новых ситуациях |
Указанные структурные компоненты составляют одну систему и находятся во взаимной тесной связи [5].
Таким образом, мы видим, что степень компетентности будущих специалистов во многом зависит от качества математической подготовки. Обучение математике, помимо задач по формированию конкретных знаний и умений, должно быть направлено на совершенствование общих компетенций будущего специалиста.
Библиографическая ссылка
Торогелдиева К.М., Алиева Ч.М. КОМПЕТЕНТНОСТНЫЙ ПОДХОД В ОБУЧЕНИИ МАТЕМАТИКЕ КАК ОСНОВА ПРОФЕССИОНАЛЬНОЙ ПОДГОТОВКИ СТУДЕНТОВ ЭКОНОМИЧЕСКИХ КОЛЛЕДЖЕЙ // Международный журнал экспериментального образования. 2017. № 6. С. 66-70;URL: https://expeducation.ru/ru/article/view?id=11694 (дата обращения: 02.03.2026).

