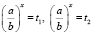В школьном курсе алгебры уравнения занимают важное место. Линия уравнений и неравенств основана на построении и изучении математических моделей, включает вырабатывание и совершенствование техники алгебраических преобразований для решения уравнений, неравенств и систем. В процессе изучения данной темы у учащихся формируются способности строить и исследовать математические модели при решении задач из смежных дисциплин. Значительное большинство задач о количественных отношениях и о пространственных формах окружающей действительности решается с помощью уравнений. Уравнения являются существенной частью математических средств, используемых в математическом моделировании. Установление междисциплинарных связей в образовательной практике ведет к качественному развитию общекультурных компетенций [1].
Согласно программе для классов с углубленным изучением математики в результате изучения данной дисциплины учащиеся должны научиться решать различные уравнения и использовать приобретенные знания, умения и навыки в практической деятельности. С целью овладения указанным видом учебной деятельности обучающийся в ходе освоения математики должен обладать определенными способностями (табл. 1).
Таблица 1
Способности, которыми должен обладать ученик в ходе освоения математики
|
понимать: |
- термины «уравнение», «система уравнений», «корень уравнения», «решение уравнения», «решение системы уравнений» в тексте задач, в речи учителя; - уравнения – это математическая модель решения различных задач из математики, смежных наук, практики |
|
знать: |
- определения различных видов уравнений; - теоремы о равносильности уравнений; - основные приемы решения уравнений; - общие методы решения уравнений |
|
уметь: |
- решать линейные, квадратные, рациональные, показательные, логарифмические, тригонометрические уравнения; - решать системы уравнений с двумя неизвестными; - решать уравнения с параметрами; - изображать на координатной плоскости решения уравнений, неравенств и систем с двумя неизвестными; - решать текстовые задачи с помощью составления уравнений [2] |
|
использовать приобретенные знания и умения в практической деятельности: |
- для построения и изучения простейших математических моделей |
Цель исследования состоит в разработке научно обоснованных методических рекомендаций по обучению учащихся естественнонаучного профиля решению уравнений.
Объект исследования: процесс обучения алгебре в классах естественнонаучного профиля.
Предмет исследования: методическая система обучения учащихся решению уравнений [3].
В соответствии с поставленной целью были определены задачи исследования:
1. Проанализировать научно-методическую литературу по теории уравнений с целью выявления теоретических аспектов формирования умений решать уравнения при обучении математике.
2. Изучив математическую литературу, выделить логико-математические основы решения уравнений.
3. Разработать общие рекомендации по методике обучения школьников решению уравнений.
Логико-математические основы решения уравнений
Теоретической основой решения уравнений является равносильность уравнений. В табл. 2 приведены основные определения и теоремы о равносильности.
Таблица 2
Определения и теоремы о равносильности
|
Определения |
1. Если множества корней уравнений f(x) = g(x) и p(x) = h(x) совпадают, то их называют равносильными. 2. Уравнение p(x) = h(x) называют следствием уравнения f(x) = g(x), если все корни уравнения f(x) = g(x) являются корнями уравнения p(x) = h(x) |
|
Теоремы |
Уравнение равносильное данному уравнению получится при следующих алгебраических преобразованиях: 1. Перенос любого члена уравнения из одной части уравнения в другую с противоположным знаком. 2. Умножение обеих частей уравнения f(x) = g(x) на одно и то же число, отличное от нуля. 3. Умножение обеих частей уравнения f(x) = g(x) на одно и то же выражение h(x), которое: 1) всюду в области определения уравнения f(x) = g(x) имеет смысл; 2) нигде в этой области не обращается в 0. 4. Возведение обеих частей уравнения f(x) = g(x) в одну и ту же нечётную степень. 5. Возведение обеих частей уравнения f(x) = g(x) в одну и ту же чётную степень, при условии, что обе части уравнения неотрицательны в области определения уравнения. 6. Переход от показательного уравнения 7. Переход от логарифмического уравнения |
Рассмотрим общие принципы решения уравнений. Существует три этапа решения уравнений. Первый этап – технический. На данном этапе осуществляется переход к новому уравнению f1(x) = g1(x) или дизъюнкции уравнений f1(x) = g1(x), f2(x) = g2(x),… fn(x) = gn(x).
Для решения уравнения f(x) = g(x) нужно решить все уравнения f1(x) = g1(x), f2(x) = g2(x),… fn(x) = gn(x) и взять объединение множеств их корней.
Второй этап – анализ решения. На этом этапе анализируются все проведённые преобразования на равносильность.
На третьем этапе осуществляется проверка. Если, анализируя преобразования на втором этапе, делается вывод, что получено уравнение-следствие, то проводится проверка всех найденных корней их подстановкой в уравнение f(x) = g(x). В результате мы и получаем множество всех корней уравнения [4].
Если какое-либо из уравнений fk(x) = gk(x) не решается непосредственно, то к нему применяется тот же прием.
Существуют четыре общих универсальных метода решения уравнений: функционально-графический метод, метод введения новой переменной, метод разложения на множители, метод решения однородных уравнений. Каждый из этих методов решения уравнения подходит для решения любого типа уравнений. В этом их сила и универсальность. В таблице приведены общие методы решения уравнений.
Общие методы решения уравнений
Метод разложения на множители
Суть метода: пусть нужно решить уравнение f(x) = 0 и пусть 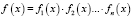 . Тогда уравнение f(x) = 0 можно заменить совокупностью более простых уравнений
. Тогда уравнение f(x) = 0 можно заменить совокупностью более простых уравнений
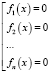 .
.
Находим корни уравнений этой совокупности, далее отобрав из них те, что принадлежат области определения уравнения f(x) = 0, получим корни уравнения f(x) = 0.
Приемы разложения: вынесение общего множителя за скобки; способ группировки; использование формул сокращенного умножения, разложение квадратного трехчлена
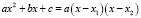 ,
,
где x1 и x2 – корни квадратного трехчлена. Иногда добавляется искусственный прием: представление одного из слагаемых в виде некоторой суммы и, в частности, прибавление и вычитание одного и того же выражения с целью последующей перегруппировки слагаемых; всевозможные комбинации вышеуказанных приемов.
Функционально-графический метод
Суть метода: необходимо построить графики функций y = f(x), y = g(x) и найти точки их пересечения. Корнями уравнения служат абсциссы этих точек. Данный метод позволяет определить число корней, угадать значение корня, найти приближенное, а иногда и точное значение корней.
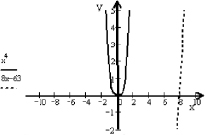
Решение уравнения графическим методом
Пример. Решим уравнение x4 – 8x + 63 = 0. Представим исходное уравнение в виде x4 = 8x – 63. Построим графики функций y = x4, y = 8x – 63.
Графики не пересекаются, а значит, исходное уравнение не имеет корней.
Ответ: нет корней.
В некоторых случаях построение графиков функций можно заменить ссылкой на какие-либо свойства функции (монотонность).
Метод введения новой переменной
Суть метода: если уравнение f(x) = 0 удалось преобразовать к виду f(g(x)) = 0, то надо ввести новую переменную y = g(x), решить уравнение f(y) = 0, далее необходимо решить совокупность уравнений
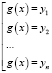 ,
,
где 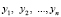 – корни уравнения f(y) = 0.
– корни уравнения f(y) = 0.
Приведем пример.
Решим уравнение
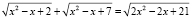 .
.
Положив y = x2 – x, получим
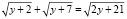 .
.
Далее имеем последовательно
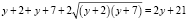 ,
,
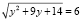 ,
, 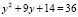 ,
,
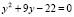 ,
, 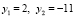 .
.
Проверка найденных значений подстановкой в исходное уравнение показывает, что y1 = 2 удовлетворяет этому уравнению, y2 = –11 – нет, это посторонний корень. Возвращаясь к переменной х, получаем уравнение x2 – x = 0, откуда находим x1 = 2, x2 = –1.
Ответ: 2; –1.
Метод решения однородных уравнений
Однородные уравнения – термин связан с понятием однородной функции.
Функция f(x; y) от двух аргументов х и у называется однородной функцией степени n, если f(kx; ky) = kn·f(x; y), где число n – степень однородной функции f(x; y).
Однородным уравнением одной переменной первого порядка называется уравнение вида
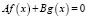 ,
,
где f(x) и g(x) – функции одного вида.
Однородным уравнением одной переменной второго порядка называется уравнение вида
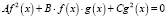 ,
,
где f(x) и g(x) – функции одного вида.
Метод решения рассмотрим на примере показательных уравнений (табл. 3).
Таблица 3
Методы решения однородных уравнений
|
Название |
Однородное уравнение первой степени |
Однородное уравнение второй степени |
|
Общий вид |
|
|
|
Суть метода решения |
1) разделить обе части уравнения на bx, где bx ≠ 0; 2) обозначить 3) решив линейное уравнение 4) проверить условие t > 0; 5) решить уравнение |
1) разделить обе части уравнения на b2x, где b2x ≠ 0; 2) обозначить 3) решив квадратное уравнение 4) проверить условие t > 0; 5) решить уравнения |
Пример. Решим уравнение
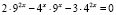 .
.
Решение:
1) 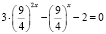 ;
;
2) обозначим 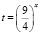 , t > 0;
, t > 0;
3) получим квадратное уравнение
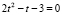 ,
, 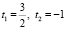 ;
;
4) t2, не удовлетворяет условию t > 0;
5) 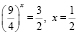 . Ответ:
. Ответ: 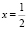 .
.
Общие рекомендации по методике обучения школьников решению уравнений
Обучение решению уравнений начинается с простейших их видов. Учебная программа создает условия для постепенного накопления как видов уравнений, так и «фонда» тождественных и равносильных преобразований, с помощью которых можно привести произвольное уравнение к простейшим.
На основе анализа теоретико-методических основ изучения уравнений в школьном курсе сформулируем этапы обучения школьников решению уравнений [5–6].
1. Вводится определение конкретного вида уравнений.
2. Решаются простейшие уравнения данного вида.
3. Анализируются действия, необходимые для их решения.
4. Выводится алгоритм решения простейших уравнений.
5. Решаются несложные уравнения данного вида, не являющиеся простейшими.
6. Анализируются действия, необходимые для их решения.
7. Применяются общие методы решения уравнений к данному виду уравнений.
8. Выводится алгоритм решения данного вида уравнений общими методами решения уравнений.
9. Формулируются частные методы решения уравнений, которые подходят только к данному виду уравнений.
10. Выводится алгоритм решения уравнений частными методами.
11. Анализируются полученные частные приемы, выделяются в их составе общие действия.
12. Формулируется обобщенный прием решения уравнений.
Выводы
Чтобы формировать умения решать уравнения, необходимо обучать способам решения уравнений. Каждый способ решения уравнений состоит из отдельных действий, следовательно нужно формировать умения у школьников выполнять действия, адекватные поиску способа решения и решению уравнения. На основе анализа теоретико-методических основ изучения уравнений в школьном курсе нами были сформулированы этапы обучения школьников решению уравнений.
Библиографическая ссылка
Григорян М.Э., Болдыревский П.Б., Залесский М.Л., Троицкий Р.В. ТЕОРИЯ И МЕТОДИКА ОБУЧЕНИЯ ШКОЛЬНИКОВ РЕШЕНИЮ УРАВНЕНИЙ // Международный журнал экспериментального образования. 2017. № 8. С. 28-33;URL: https://expeducation.ru/ru/article/view?id=11738 (дата обращения: 16.02.2026).


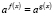 , где a > 0, a≠ 1 к уравнению f(x) = g(x).
, где a > 0, a≠ 1 к уравнению f(x) = g(x).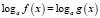 , где a > 0, a ≠ 1, к уравнению f(x) = g(x), если f(x) > 0 и g(x) > 0 [4]
, где a > 0, a ≠ 1, к уравнению f(x) = g(x), если f(x) > 0 и g(x) > 0 [4]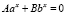 ;
;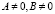
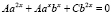 ;
;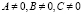
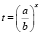 , t > 0;
, t > 0;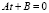 , получить корень t.
, получить корень t.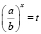
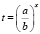 , t > 0;
, t > 0;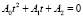 получить корни t1, t2;
получить корни t1, t2;