Методологической основой реализации требований Федерального государственного образовательного стандарта (далее – ФГОС [1]) общего образования к личностным, метапредметным и предметным результатам освоения курса математики является системно-деятельностный подход [2]. Его сущность состоит в том, что обучающийся должен стать активным субъектом образовательного процесса; целью системно-деятельностного подхода является развитие мотивации к обучению и формирование навыков самообразования; наконец, его результатом являются способности обучающегося чётко формулировать цели любой деятельности, самостоятельно осуществлять алгоритм действий, направленных на получение знаний и решение поставленных перед ними учебных задач (cм. [2], [3]) .
Само название данного подхода говорит о лежащих в его основе принципах системности и деятельности. Первый из них состоит в целостности, полноте, комплексности, связности получаемой школьником информации. Средствами его реализация являются: метод межпредметности, практической ориентированности получаемого знания; систематизация получаемой информации возможна путём составления схем, таблиц, построения графиков, диаграмм, использования математической символики.
Принцип деятельности состоит в создании условий, при которых учащиеся не просто получают готовую информацию, а сами, пользуясь разнообразными источниками, извлекают её и применяют затем на практике.
Согласно ФГОС, результаты применения системно-деятельностного подхода в обучении математике можно разделить на 3 группы: личностные, метапредметные и предметные. Соответственно, возникает вопрос о видах деятельности, обеспечивающих успешную реализацию системно-деятельностного подхода и достижение названных результатов в области обучения математике. Нам представляется, что такими видами являются:
– постановка задач, приводящих к новым для учащегося понятиям и фактам;
– проектирование способов, схем и алгоритмов их решения;
– применение методов и приёмов, направленных на активизацию познавательной деятельности учащихся в процессе решения поставленных задач;
– организация сотрудничества между учащимися и индивидуальной работы каждого из них (формирование коммуникативных умений);
– формулировка выводов, гипотез, обобщений и рефлексия деятельности: самостоятельная оценка учащимися результатов своей работы, подведение её итогов;
– межпредметная и практическая ориентированность знаний и умений, что достигается постановкой практических задач из реальной жизни, задач на стыке предметов.
Перечисленные виды деятельности могут быть объединены категорией «задачный подход».
Задачный подход есть специально организованное и систематически осуществляемое обучение в виде разрешения разнообразных учебных задач. Общая теория задачного подхода представлена в монографии [4]. Сформулируем те положения задачного подхода, которые представляются нам наиболее важными с точки зрения принципов системности и деятельности:
– введение новых понятий предваряется постановкой некоторой задачи;
– новое знание формируется в процессе решения задачи;
– результатом решения является «выход» в сферу применений нового знания как в самой предметной области «Математика», так и в смежных дисциплинах, а также в практической деятельности;
– решённая задача порождает серию новых задач (данный результат мы именуем «принципом снежного кома»), что способствует расширению и углублению сформированного знания, усилению мотивации математической деятельности, формированию способностей к обобщению и систематизации результатов.
Задачный подход является альтернативой традиционному знаниевому подходу, когда необходимый объём знаний передаётся в готовом виде, так что учащемуся остаётся лишь осознать и запомнить полученный объём информации; здесь «единицей обученности» выступает некоторая единица информации. В то же время результат задачного подхода измеряется в таких единицах обученности, как интеллектуальное умение, способность давать ответы на соответствующие вопросы, применять усвоенные способы деятельности в новых условиях.
Продемонстрируем, как реализуется вышеупомянутый «принцип снежного кома» на примере следующей задачи.
Сформулировать условия на коэффициенты p, q квадратного трёхчлена y = x2 + px + q, при которых оба его корня являются положительными действительными числами.
В процессе анализа задачи учащиеся формулируют условие существования действительных корней и, опираясь на теорему Виета, приходят к системе требований положительности произведения и, одновременно, суммы корней:
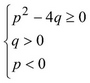
Далее следует развитие ситуации: возникает вопрос об условиях отрицательности корней, условиях, обеспечивающих наличие корней разных знаков. Наконец, формулируется обобщенная задача: при каких условиях на коэффициенты квадратного трёхчлена оба корня:
а) больше (не меньше) заданного действительного числа;
б) меньше (не больше) заданного действительного числа;
в) один из них больше (не меньше), а другой меньше (не больше) заданного действительного числа.
Решая первоначальную, а затем и обобщенную задачу о корнях квадратного трехчлена, учащийся овладевает методом оценки корней квадратного трёхчлена числовой оси с помощью анализа расположения соответствующей параболы на координатной плоскости, что отвечает целям формирования предметных результатов. В то же время здесь формируется умение рассматривать все возможные ситуации, задавать вопросы, усматривать аналогии, создавать обобщения, что находится в русле развития соответствующих общеучебных умений, а значит, способствует достижению определённых метапредметных результатов. Наконец, всестороннее изучение возникающих ситуаций и выработка общих подходов к их анализу способствует формированию целостного мировоззрения, системного мышления, что можно отнести к личностным результатам.
Рассмотрим теперь отдельные, эффективные, с нашей точки зрения, технологические приёмы обучения математике в рамках реализации задачного подхода.
Теоретические упражнения
Речь идёт о некоторых общих математических фактах (формулах, «мини-теоремах» и т.п.), которые устанавливают сами учащиеся. Соответствующая деятельность учащегося состоит в накоплении и анализе фактов, выдвижении гипотез, их подтверждении путём проведением соответствующего доказательства либо опровержении путём построения контрпримеров, решении стандартных задач в общем виде и др.
Так, например, сравнивая сумму квадратов сторон треугольника с квадратом третьей его стороны, учащийся приходит к следующей гипотезе: если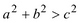 
, то угол, заключенный между сторонами a и b – острый, если 
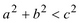– то угол тупой; если же 
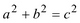, то этот угол прямой (утверждение, обратное теореме Пифагора). Затем следует поиск средства доказательства указанного факта и самостоятельное проведение учащимися соответствующего доказательства.
Приведём другие примеры теоретических упражнений:
1) докажите, что высота h, проведённая к гипотенузе c прямоугольного треугольника с катетами a и b, может быть найдена по формуле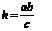 
;
2) вычислите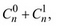 
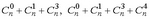
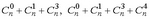. Какую закономерность вы обнаруживаете? Сформулируйте и докажите соответствующий результат в общем виде.
В результате решения данного упражнения учащийся должен «увидеть», а затем доказать соотношение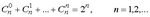 
, где 
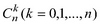– число сочетаний из n по k 
;
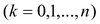3) докажите равносильность следующих формул вероятности суммы двух совместных независимых событий
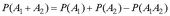
и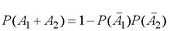 
.
Практико-ориентированной мы называем задачу, которая
1) имеет сюжет, отражающий некоторую практическую ситуацию;
2) допускает математическую формализацию (переформулирование в математических терминах);
3) решается (в формализованном виде) математическими средствами;
4) допускает интерпретацию полученного решения, дающую ответ на изначально поставленный вопрос.
Практико-ориентированная математическая подготовка направлена на использование математики в решении широкого круга проблем, возникающих в реальном мире за пределами образовательного процесса. Практико-ориентированные задачи призваны выполнять следующие важные функции:
– обеспечение познавательной мотивации учащихся;
– формирование системы межпредметных знаний и умений;
– приобретение опыта использования результатов теоретического исследования в практической деятельности.
Мы выделяем следующие классы прикладных и практико-ориентированных задач:
– задачи на визуализацию информации (например, чтение графиков или, наоборот, построение графика заданного процесса);
– задачи на нахождение долей, процентов;
– простейшие финансовые задачи и задачи на оптимизацию финансовой деятельности (наиболее выгодная схема вложения денег, оптимальная схема погашения кредита, выбор наиболее дешевого варианта получения услуги и т.п.);
– нахождение углов, длин отрезков на «квадратной решетке» и в системе координат, площадей нестандартных фигур, объемов нестандартных тел;
– задачи прикладной геометрии (например, нахождение расстояний до недоступных объектов на местности на основании некоторых «доступных» результатов измерений);
– задачи на проценты; задачи на смеси и сплавы;
– задачи на равномерное движение (встречное движение и движение в одном направлении; движение по реке, движение по окружности и др.);
– задачи на совместную работу;
– анализ закономерностей, заданных в форме последовательности (в частности, прогрессии);
– прикладные задачи (например, задачи физического содержания), требующие анализа аналитически заданной зависимости;
– задачи максимизации (минимизации);
– «численное прогнозирование» (задачи теории вероятностей);
– анализ эмпирических распределений (задачи математической статистики).
Решение задач каждого из указанных типов, помимо развития собственно предметных умений, способствует развитию общеучебных умений учащихся, поскольку соответствующая их деятельность приобретает исследовательский, прикладной и практико-ориентированный характер.
Каждая практическая или прикладная задача, решаемая средствами математики, сопровождается переводом ее условия на математический язык и последующим использованием понятий, фактов и методов математической науки. Указанный процесс является не чем иным, как процессом математического моделирования [5].
Модели, изучаемые в школьном курсе, подразделяются:
1) на детерминированные модели; здесь исследователь исходит из предположения отсутствия всяких случайных воздействий; поведение объекта или процесса можно точно определить. Используемый математический аппарат – алгебра, геометрия, математический анализ;
2) стохастические модели, которые описывают случайный характер процессов в исследуемых объектах и системах; используемый математический аппарат – теория вероятностей, математическая статистика, теория случайных процессов.
Задачный материал
Поясним на следующем примере, как происходит процесс исследования детерминированных моделей.
Двум проектным организациям поручается выполнить 43 разработки, при этом 23 финансируются из бюджетных средств, а 20 – из внебюджетных фондов; при этом первой организации предстоит разработать 21 проект. Каково должно быть распределение проектов, чтобы суммарный процент разработок, финансируемых из средств бюджета, в задании обеих организаций, оказался наибольшим.
1 шаг решения: формализация ситуации, описываемой условием задачи. Пусть первой организации поручено х «бюджетных» проектов (где 1 ≤ x ≤ 21), тогда второй – 23 – x) проектов. Доли «бюджетных» разработок тогда составили соответственно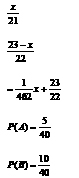 
и 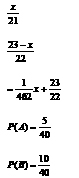. Значит, суммарная их доля равна
+ = .
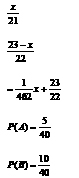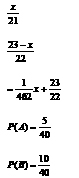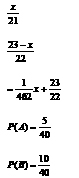Получена задача о нахождении наибольшего значения функции
y.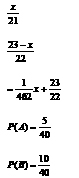
2 шаг: решение математической задачи. Имеем линейную функцию с положительным коэффициентом перед х. Значит, эта функция достигает своего наибольшего значения на правом конце промежутка [1; 21], то есть при x = 21.
3 шаг: интерпретация результата: первая организация полностью выполняет проекты, финансируемые из бюджета, тогда как вторая организация должна выполнить две «бюджетные» разработки и 20 внебюджетных.
Отметим, что решение подобных задач на оптимальный выбор требует комплексного применения математических знаний и умений (в данной задаче: нахождение долей, конструирование функции, исследование на наибольшее значение), что в конечном итоге способствует формированию системного мышления.
Продемонстрируем на примере стохастической модели, как решение задачи приводит к введению нового понятия (здесь – геометрической вероятности). Человек Рассеянный с улицы Бассейной в отцепленном вагоне проснулся ночью и обнаружил, что его часы остались дома. Что вероятнее: что сейчас часы показывают от половины первого до половины второго ночи или от двух до четырёх часов?
Естественным образом выстраивается следующая формализация модели: следует сравнить численные меры степени объективной возможности обоих событий, подобрав подходящий способ нахождения вероятности. В данном случае надо сравнить два отношения, а именно, сравнить отношения длин соответствующих дуг окружности циферблата (на которых должен находиться конец часовой стрелки), к длине части окружности, соответствующей времени сна.
Если принять время сна Человека Рассеянного, например, от 10 вечера до 6 утра (то есть сна в течение 8 часов), то это время соответствует дуге окружности циферблата длиною в 40 делений, пробегаемых часовой стрелкой. В первом случае (событие А: часы показывают от половины первого до половины второго ночи) дуга окружности, на которой находился бы конец часовой стрелки, составляет 5 делений, во втором (событие В: от двух до четырёх часов ночи) – 10 делений. 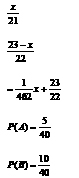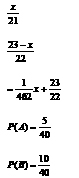Отношения и следует теперь принять за соответствующие вероятности.
Интерпретация модели: второе событие вероятнее (что, впрочем, было ясно изначально на основе интуитивных соображений, но теперь подтверждено математически).
На основе решения данной задачи выстраивается геометрический подход к понятию вероятности, то есть задачный подход способствует возникновению новой для учащегося геометрической модели понятия вероятности и побуждает к исследованию свойств этой модели.
Выводы
Подводя краткий итог сказанному, мы усматриваем выстраивание следующей схемы реализации требований ФГОС в области математического образования:
ФГОС 
системно-деятельностный подход 
задачный подход.
В рамках задачного подхода мы предлагаем такие технологические приёмы обучения математике, как решение теоретических упражнений и практико-ориентированных задач. Данные приёмы нацелены на достижение как предметных, так и метапредметных и личностных результатов, среди которых – формирование познавательной мотивации обучения, системы межпредметных знаний и умений, приобретение опыта использования результатов теоретического исследования в практической деятельности.
Библиографическая ссылка
Нахман А.Д. ЗАДАЧНЫЙ ПОДХОД КАК ТЕХНОЛОГИЧЕСКАЯ ОСНОВА ПРОЦЕССА ОБУЧЕНИЯ МАТЕМАТИКЕ // Международный журнал экспериментального образования. – 2018. – № 2. – С. 34-39;URL: https://expeducation.ru/ru/article/view?id=11793 (дата обращения: 19.04.2024).