Использование статистических приемов упорядочения, представления и принятия решений на основе массивов данных давно и глубоко вошло в практику педагогических исследований ([1–3] и др). Огромный арсенал приемов, накопленный в прошлом веке (и автоматизированный в программном обеспечении), позволяет обрабатывать одномерные и многомерные массивы количественных данных, выборки больших и малых объемов, сравнивать выборки разных объемов и оценивать сдвиги в связанных выборках, исследовать временные ряды, выделяя в них линейные и циклические компоненты и т.д. Кроме проблем, идеологически связанных с математическим моделированием (например, [4]), огромное значение для успеха статистического исследования имеют происхождение обрабатываемых эмпирических или имитированных данных и логика построения исследования. Очевидно, что преимуществом обладают такие данные, которые получены «естественным» путем наблюдения, а не под влиянием исследователя – экспериментатора, способного, пусть и непреднамеренно, исказить оценки в пользу имеющейся у него педагогической гипотезы.
Особенностью современного педагогического взаимодействия в техническом вузе является его «электронный след», что открывает богатые возможности для исследования закономерностей педагогической и учебной жизни путем наблюдения. Ещё совсем недавно основным документированным источником, характеризующим академическую успешность студента, были оценки, полученные в сессию. Отметим, что преподаватели, оценивающие студентов, находятся под давлением локальных нормативов, администрации и других существенных факторов, и сама оценка по дисциплине за семестр – достаточно сложный феномен. Можно было обратиться к текущим оценкам или отметкам, но сравнение успеваемости разных категорий студентов по этим результатам сильно затруднено различиями в номенклатуре текущих контрольных мероприятий. Обращение в исследовательских целях к самим работам представляется практически невыполнимым из-за существования разных версий каждой работы, проходящей сложный путь через рецензирование и исправление недочетов, графических и рукописных элементов. Альтернативой выступали результаты тестирования, опросов и других специально организованных обследований, но они требовали дополнительных усилий и в планировании, и в проведении, и в оценке валидности. Сейчас большое количество «даровых» данных (часто в удобной для преобразований цифровой форме), характеризующих педагогическое взаимодействие, накапливается естественным путем и может являться предметом научного изучения.
Составление формализованного электронного портфолио, в котором регламентирован состав элементов и их атрибуты, – достаточно широко распространенная процедура в российских университетах, она вводится по инициативе преподавателей или административных структур с целью фиксации разнообразных студенческих достижений для возможности в дальнейшем сравнивать их или презентовать при внешних проверках. С другой стороны, в доступной литературе ([5–7] и др.) имеются исследования, посвященные этому инструменту как средству повышения активности студентов, наряду с балльно-рейтинговой системой и тестированием ([8] и др.), в цифровизованном учебно-воспитательном процессе. Как массовый процесс, составление такого портфолио не зависит от предметной сути изучаемой дисциплины, но отражает способность студентов адекватно понимать инструкции и выдвигаемые общие требования, готовность им следовать, используя «обратную связь» по предоставленным каналам коммуникации. Несложные приемы фиксации времени представления портфолио на проверку и статистической обработки полученных данных позволили наглядно продемонстрировать и сравнить особенности выполнения этого несложного задания потоками студентов заочной формы обучения в первую сессию и опытных студентов очной формы обучения.
Понимание особенностей выполнения и предъявления одинаковых заданий студентами с разным учебным опытом помогает осознанному переносу и адаптации организационных и методических решений при организации аналогичных учебных курсов. Мы наблюдаем поступательную унификацию внешних требований к тематическому содержанию преподаваемых дисциплин, осложненную изменениями способов осуществления педагогического взаимодействия, и применяемые в преподавании «гибкие педагогические технологии» нуждаются в надежном фактическом фундаменте. В [9] предлагается немного подождать, когда в каждую аудиторию придут технологии обработки «больших данных» и некоторым чудесным образом предложат решения актуальных методических задач. Однако в данном исследовании мы стремимся получить такие факты в результате обобщения данных (наблюдений), полученных в живом учебном процессе.
Материалы и методы исследования
Каждая попытка представления формального портфолио на проверку через интерактивную электронную среду Blackboard Learn автоматически фиксируется по времени, что позволяет в результате педагогического взаимодействия накопить массивы данных и подвергнуть их потом обработке.
Для нашего исследования были взяты: данные потока студентов 2 курса специальности «Эксплуатация железных дорог» очной формы обучения (в дальнейшем будем называть их «опытные очники» – 133 чел.) за зимнюю сессию и аналогичные данные потока студентов 1 курса заочной формы обучения (далее – «неопытные заочники» – 65 чел.). Учитывалось время каждой попытки представления портфолио на проверку и количество попыток представления до достижения успеха каждым студентом.
В исследовании использовали построение дифференциальных и накопительных гистограмм; критерий «хи-квадрат» (Пирсона) для проверки соответствия эмпирической функции распределения гипотетическому закону, многофункциональный критерий φ* (Фишера) для сравнения долей проявления признаков в выборках.
Для расчетов использовали MS Excel 2007.
Результаты исследования и их обсуждение
Для наглядного представления распределения попыток сдачи задания по срокам мы построили гистограммы относительных частот количества попыток предъявления портфолио на проверку (в отношении к общему числу попыток в потоке), где каждый интервал – 3 календарных дня (рис. 1).
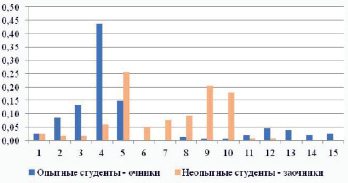
Рис. 1. Распределение попыток по сроку (от начала кампании)
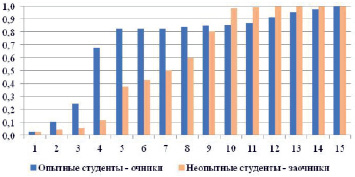
Рис. 2. Накопительная гистограмма распределения попыток по сроку
В обоих случаях за начало отсчета взят срок, когда появились регулярные ежедневные попытки предъявления задания студентами. На графиках видно, что динамика у процесса разная, но в обоих случаях видны две «волны». У очников это допуск на первый зачет и доработка в сессию. У заочников это последние дни перед сессией и дни промежуточной аттестации.
Дополнительно мы предлагаем рассмотреть накопительную гистограмму, иллюстрирующую эти распределения (рис. 2).
Как видим, к концу второй недели кампании (на пятом интервале) опытные студенты очной формы обучения уже сделали 80 % попыток предъявления задания на проверку и после этого поступление новых попыток резко ослабло. А студенты заочной формы обучения достигают такого показателя лишь к концу четвертой недели (на 9 интервале), однако общая протяженность кампании у них оказалась меньше.
Для иллюстрации количества попыток, сделанных каждым студентом, мы также построили гистограммы относительных частот (рис. 3).
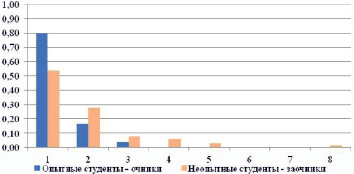
Рис. 3. Распределение студентов по количеству попыток до успеха
Таблица 1
|
Опытные очники |
Неопытные заочники |
||||
|
p = 0,8; k = 1; α = 0,05 |
p = 0,54; k = 2; α = 0,05 |
||||
|
наблюдаемые |
ожидаемые |
наблюдаемые |
ожидаемые |
||
|
1 |
106 |
106,4 |
1 |
35 |
35,100 |
|
2 |
22 |
21,28 |
2 |
18 |
16,146 |
|
>2 |
5 |
5,32 |
3 |
5 |
7,427 |
|
сумма |
133 |
>3 |
7 |
6,327 |
|
|
χ2набл |
0,045 |
сумма |
65 |
||
|
χ2кр |
3,8 |
χ2набл |
1,078 |
||
|
χ2кр |
6 |
||||
Вид гистограммы позволяет выдвинуть и проверить с помощью «хи-квадрата» критерия Пирсона статистическую гипотезу о геометрическом законе распределения обеих выборок, предполагающего одинаковую вероятность успеха (в каждой попытке) независимо от её номера [10]. В таком случае нулевая гипотеза: количество попыток сдачи задания подчиняется геометрическому закону распределения. Альтернативная гипотеза: количество попыток сдачи задания не подчиняется геометрическому закону распределения.
«Вероятности успеха в единичном испытании» для теоретических геометрических распределений были получены методом наибольшего соответствия. По формулам геометрического распределения нашли ожидаемые теоретические частоты. Затем с помощью критерия «хи-квадрат» убедились, что гипотеза о геометрическом распределении (с данными значениями вероятностей успеха) верна, как в обоих случаях наблюдаемое значение статистики «хи-квадрат» меньше критического (табл. 1).
Дополнительно обратим внимание на то, какая доля студентов выполняет задачу с первого раза. Свойство геометрического распределения состоит в том, что ожидаемая доля таких случаев численно совпадает со значением параметра р распределения, то есть 0,80 для первой выборки и 0,54 – для второй выборки (теоретические и эмпирические данные хорошо совпали). Применяя многофункциональный метод, известный как «угловое преобразование Фишера» (или φ* тест Фишера) [11], для данных объемов выборки, можно убедиться в статистически значимой разнице этих долей: статистика φ*, характеризующая различие выборок, показала значение φ*эмп = 3,72 и существенно превысила критическое значение φ*кр = 2,31.
Заключение
1. Общие черты процессов сдачи одинакового несложного задания у студентов очной и заочной форм обучения:
– по срокам сдачи в динамике процесса наблюдаются две «волны» возрастания интенсивности попыток предъявления задания;
– количество попыток сдачи задания подчиняется геометрическому закону распределения.
2. Особенности процессов сдачи задания у студентов с разным учебным опытом для наглядности представлены в табл. 2.
Таблица 2
|
Опытные очники |
Неопытные заочники |
|
Особенности по интенсивности и общей протяженности кампании |
|
|
Предъявляют на проверку портфолио в начале кампании с большой интенсивностью, а затем она значительно снижается |
Наибольшая интенсивность наблюдается в середине кампании, в первые и последние дни – практически нулевая |
|
Протяженность 45 дней |
Протяженность 36 дней |
|
Особенности по вероятности успеха и математическому ожиданию количества попыток M(X) = 1/p(X) |
|
|
p1 = 0,80 M(X1) = 1,25 |
p2 = 0,54 M(X2) = 1,85 |
Рассмотренные ситуации можно расценивать как некоторые полюсы, между которыми расположены промежуточные варианты. Например, предполагаемые неопытные очники объективно имеют преимущество перед заочниками в силу более интенсивного взаимодействия с представителями профессорско-преподавательского корпуса и деканата, даже подходя к первой сессии, они лучше понимают, что от них требуют, и предвидят, как будут проверяться результаты выполнения заданий. Заочники, пусть медленней, но проходят аналогичный путь адаптации к требованиям среды и со временем показывают сравнимую успешность в выполнении аналогичных элементарных заданий (как известно, профессиональный и социальный опыт даже дает им преимущество перед очниками в сложной деятельности с неясным исходом).
Дополнительно отметим, что сравнение успешности, различия или особенности выполнения сходных учебных задач разными категориями учащихся достаточно редко становятся самостоятельным предметом объективного статистического исследования. Мы (в основном) связываем этот факт с тем, что подходящие для обработки массивы данных, единство условий для наблюдений в сочетании с документальной фиксацией результатов возникают естественным образом, но теряются как побочный продукт педагогического взаимодействия. А специально организованные обследования требуют и особых организационных и методических усилий, и встречной административной поддержки.
Библиографическая ссылка
Гончарь П.С., Нематова Е.Д., Петухова Ю.С. ЭЛЕКТРОННОЕ ПОРТФОЛИО ДЛЯ СТУДЕНТОВ УНИВЕРСИТЕТА С РАЗНЫМ УЧЕБНЫМ ОПЫТОМ // Международный журнал экспериментального образования. 2021. № 1. С. 47-51;URL: https://expeducation.ru/ru/article/view?id=12012 (дата обращения: 01.01.2026).

