Инновационные процессы, происходящие в российской системе образования на всех ее уровнях и инициированные обновленными Федеральными государственными образовательными стандартами (ФГОС), в значительной степени затрагивают математическое образование. Так, согласно требованиям ФГОС основного общего образования [1], изучение предметной области «Математика и информатика» должно обеспечить развитие у обучающегося логического и математического мышления, овладение математическими рассуждениями, формирование представлений о математических моделях и умений применять математические знания при решении различных задач.
В этой связи сами задачные системы должны быть соответствующим образом модернизированы. Прежде всего, необходимо наличие именно системных свойств; это означает, что задания подобраны в соответствии с поставленной («глобальной» или «локальной») целью, и их взаимосвязь и взаимодействие приводит к намеченному результату ([2–4] и библиография в них).
В нашем понимании, конструируемые задачные системы приобретают признаки инновационности [5], если в них имеется соответствующая потребность, а сами они являются в определенной степени новыми, апробированными, могут быть внедрены (или уже внедрены) и «диффундированы» в образовательную практику [6].
Так, например, предлагаемые ниже задачи-трансформеры конструируются с целью способствования интеграции вероятностно-статистического модуля в общую систему математической подготовки (глобальная цель) и, в частности, направлены на реализацию методов математического анализа при моделировании стохастических ситуаций (локальная цель, [7]).
В настоящей работе мы демонстрируем и обсуждаем некоторые задания – представители предлагаемых нами инновационных задачных систем.
1. Вопросы теории и теоретические упражнения
Теоретические вопросы традиционно ориентированы на репродуктивный уровень освоения материала («сформулируйте определение, теорему» и т.п.), тогда как более высокие уровни требуют осмысления, сопоставления и противопоставления фактов, их геометрических интерпретаций и т.п. Здесь предпочтительнее формулировки типа «верно ли», «приведите пример» и др. Так, в области математического анализа вопросы могут быть, например, следующими.
1. Приведите пример функции,
а) имеющей одну точку разрыва первого рода;
б) имеющей две точки разрыва второго рода.
2. Можно ли привести пример функции,
а) непрерывной в данной точке, но не дифференцируемой в ней;
б) обладающей производной в некоторой точке, но имеющей в этой точке разрыв?
В случае утвердительного ответа приведите соответствующий пример.
3. Может ли касательная пересечь график функции в точке касания? Если ответ утвердительный, то приведите соответствующий пример.
4. Эквивалентны ли понятия максимума (минимума) функции и ее наибольшего (наименьшего) значения на данном отрезке? Если ответ отрицательный, то приведите соответствующий пример.
5. Может ли касательная, проведенная в точке минимума функции, иметь уравнение y = –0,1x? Обоснуйте ответ.
6. Всегда ли непрерывная на данном открытом интервале функция достигает своего наибольшего значения? А на отрезке непрерывности?
7. Верно ли утверждение: «Если общий член числового ряда на бесконечности имеет своим пределом число 0, то ряд сходится»? Обоснуйте свой ответ.
8. Может ли быть так, что некоторый степенной ряд сходится на промежутке [0; +∞) и расходится на (–∞; 0)? Ответ обоснуйте.
Освоению теоретических фактов в значительной мере способствуют «мини-теоремы» – теоретические упражнения, а также ключевые задачи, поставленные и решаемые в самом общем виде. Так, в ряде случаев традиционные доказательства теорем могут быть сведены к решению последовательности теоретических упражнений. Приведем примеры некоторых упражнений в области математического анализа и стохастики.
1. Пользуясь результатом
,
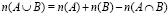вывести формулу для подсчета количества элементов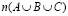 
в объединении трех множеств.
2. Каков наибольший из биномиальных коэффициентов в разложении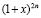 
?
3. Равны ли тождественно суммы
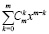и 
?
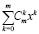4. На основании аксиом вероятности докажите, что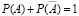 
, для всякой пары противоположных событий 
.
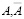5. Докажите, что выборочная средняя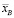 
принимает значения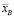 
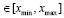, где xmax и xmin – соответственно наибольшее и наименьшее значения варианта xk .
6. Докажите, что производная функции двух переменных, вычисленная в данной точке в направлении градиента, равна модулю градиента.
7. С помощью замены переменных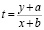 
найдите общее решение дифференциального уравнения вида
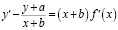
(a, b – любые постоянные величины, f – произвольная дифференцируемая на всей числовой оси функция).
2. Варьирование задач
Метод варьирования задачи состоит в получении задачной системы из некоторой «базовой» задачи путем варьирования её содержания и (или) формы. В результате получается набор заданий – «клонов», решения которых способствуют формированию упомянутых выше умений сопоставлять или противопоставлять математические понятия, методы и факты. Примером может служить задание на нахождение области определения функции вида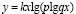 
, где k, p, q – заданные постоянные (базовое задание). А именно, требуется найти области определения функций
а)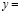 
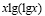
б)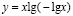 
в)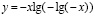
.
Приведем другие примеры заданий-клонов.
Найдите области определений функций
1. а)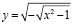 
б)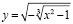 
в)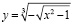 
.
2. а)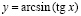 
б)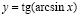 
в)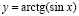 
.
Среди данных зависимостей переменной y от переменной x укажите зависимости функциональные:
1. а)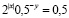 
б)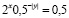 
в)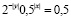 
2. а)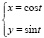 
б) 
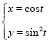в)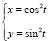 
Найдите множество всех значений функции:
а)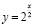 
б) 
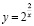в)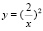 
Исследуйте данную функцию на непрерывность:
а)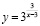 
б)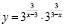 
в)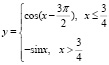 
г)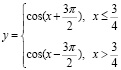 
3. Задания-кейсы
Кейсы представляют собой комплексные компетентностно-ориентированные учебные задания по моделированию различных жизненных ситуаций. Их решение требует оптимального сочетания теории и практического знания, а также умений, опирающихся на предыдущий опыт практической деятельности обучающихся. Так, например, кейс-задания представлены в составе контрольно-измерительных материалов итоговой аттестации по математике (ОГЭ) выпускников основной школы [8]. Нами разрабатываются системы стохастических кейсов ([7] и библиография в ней); приведем один из них.
В городе N имеется 10 финансовых компаний, среди которых 4 находятся на грани банкротства. Клиент выбирает для хранения и умножения средств случайным образом 2 компании. Составить ряд распределения числа Х выбранных компаний, имеющих высокий риск банкротства. Постройте многоугольник распределения. Найти математическое ожидание и среднеквадратическое отклонение случайной величины Х. С какой вероятностью можно утверждать, что хотя бы одна из выбранных компаний окажется на грани банкротства?
Решение данного кейса способствует формированию практико-ориентированных умений комплексного описания поведения случайной величины:
− умения численно прогнозировать степень возможности тех или иных значений случайной величины (вычислять вероятность извлечения выборки с заданной характеристикой объектов);
− строить ряд распределения дискретной случайной величины (ДСВ) и геометрически интерпретировать распределение;
− находить среднее значение случайной величины (математическое ожидание);
− находить числовые характеристики степени рассеяния ДСВ (дисперсию и среднеквадратическое отклонение).
4. Задачи-трансформеры и обратные стохастические задачи
Задачи-трансформеры представляют собой задания на моделирование ситуаций или процессов с целью их изучения одновременно в детерминистском и стохастическом направлении в зависимости от вопроса задачи.
Обсудим, например, следующее задание. Биржевыми аналитиками установлено, что стоимость акций компании в последний месяц года должна изменяться по закону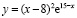 
, где х – календарная дата, x = 1, 2, …, 30 (предпраздничный день 31 декабря исключается из рассмотрения). Какого числа следует продать акции, чтобы получить максимальный доход? Какова вероятность, что в случайно выбранный день месяца стоимость акций находится на подъеме?
Очевидно, что для ответа на первый вопрос следует обратиться к детерминированной модели ситуации. Акции выгоднее всего продавать на максимуме роста, следовательно, производная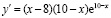 
в соответствующей точке должна изменить знак с плюса на минус. Очевидно, что такой точкой будет х = 10, то есть акции надо продать 10 декабря.
Второй вопрос предполагает наличие стохастической ситуации, поскольку выбор даты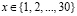 
случаен. При этом благоприятных исходов, то есть дней роста стоимости акций, всего три: 8, 9, 10 декабря. Искомая вероятность p = 3 / 30, или p = 0,1.
Решение обратных стохастических задач является эффективным технологическим приемом формирования целостности и системности знаний. Обратные задачи – важный компонент технологии укрупненных дидактических единиц (УДЕ), которая представляет собой интеграцию целого ряда конкретных подходов к обучению. Ключевой элемент технологии УДЕ – это упражнение: триада «исходная задача – ее обращение – обобщение».
С точки зрения моделирования стохастических ситуаций обратная задача представляет собою задание по нахождению некоторых входных параметров модели по ее известному выходу. Оператор модели при этом может быть полностью известен («прозрачный, белый ящик»), известен в самом общем виде, но не конкретизирован применительно к данному заданию («серый ящик»), либо полностью неизвестен («черный ящик»). Приведем пример.
Сколько раз надо бросить монету, чтобы с вероятностью р = 0,9544 утверждать, что относительная частота выпадения герба отклонилась от 0,5 не более, чем на 0,05?
«Прямая задача» состояла бы в оценке вероятности заданно малого отклонения относительной частоты m/n наступления данного случайного события от его вероятности p при заданном количестве проводимых опытов п с помощью интегральной функции Лапласа Ф(х):
;
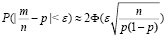в роли оператора модели выступает эта приближенная расчетная формула. В нашем случае «выход» модели известен (указанная оценка дана), а отысканию подлежит количество опытов п (служившее в прямой задаче входным параметром). Имеем
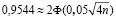
или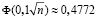 
.
Если воспользоваться таблицей значений интегральной функции Лапласа, то получим значение аргумента функции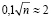 
, откуда 
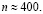Итак, монету надо бросить 400 раз.
Особого обсуждения заслуживают системы тестовых заданий, но этой теме автор надеется посвятить отдельную работу.
Заключение
Инновационные задачные системы вышеуказанных типов могут быть (как это представляется автору) в значительной степени востребованы в образовательной практике. Их решение стимулирует мотивацию к математической деятельности (таким стимулом является практическая ориентированность ряда задач), развивает исследовательские навыки (задачи-клоны), способствует становлению умений комплексного описания ситуаций и процессов (задания-кейсы, обратные стохастические задачи и задания-трансформеры) и в конечном счете способствует формированию у обучающихся целостности и системности знаний в области математики и ее приложений.
Библиографическая ссылка
Нахман А.Д. ИННОВАЦИОННЫЕ МАТЕМАТИЧЕСКИЕ ЗАДАЧНЫЕ СИСТЕМЫ // Международный журнал экспериментального образования. – 2022. – № 5. – С. 55-58;URL: https://expeducation.ru/ru/article/view?id=12097 (дата обращения: 21.11.2024).