Цикл графических дисциплин, которые изучаются при получении классического технического образования в России, начинается с изучения дисциплины «Начертательная геометрия». Начертательная геометрия закладывает основы графических знаний, изучает процесс проецирования – построения эпюра (изображения на двух перпендикулярных друг другу плоскостях) на абстрактных простых объектах, таких как точка, прямая, плоскость, поверхность. Дальнейшее графическое образование в техническом вузе студент получает при изучении инженерной и компьютерной графики.
Задачи графического образования заключаются в следующем:
− обучение процессу построения чертежа пространственного объекта (изделия: детали, сборочной единицы) в соответствии с правилами построения, регламентированными Единой системой конструкторской документации (ЕСКД);
− обучение процессу чтения чертежа – мысленному восприятию графической информации, которую содержат двухмерные изображения чертежа, и преобразованию ее в пространственный образ трехмерной детали;
− решение инженерных задач при помощи графических построений;
− развитие пространственного мышления, позволяющего преобразовывать двухмерные виды в объемный образ детали.
Цель исследования – решение задачи развития пространственного мышления в процессе изучения начертательной геометрии.
Материалы и методы исследования
Процесс пространственного мышления описан в ряде научных публикаций как особый вид умственной деятельности, обеспечивающий создание пространственных образов. Целью этого процесса является применение созданных образов в решении практических и теоретических задач [1].
Образ возникает тогда, когда работает воображение, способность человека представлять некий объект материального мира – реальный или сфантазированный.
Воображение можно определить как процесс преобразования представлений, отражающих реальную действительность, и создание на этой основе новых представлений. Различают также пространственное воображение, способность воссоздать образ в трехмерном пространстве [2].
Вообразить пространственно – это значит создать объемный трехмерный образ. Мыслить пространственно – это значит не только создать образ, а еще преобразовывать эту информацию, использовать ее для других действий в решении задач и поисках выхода при наличии проблемы.
Мышление – это рассуждение, поиск, преобразование, восприятие и изменение, формирование понятий, выработка собственных суждений [3].
Когда мы говорим о пространственном мышлении, которое формируется в процессе инженерной подготовки при изучении графических дисциплин, мы имеем в виду следующие процессы:
− процесс восприятия информации содержится в изображениях чертежа, задания – изучении заданных изображений, анализе информации и зарождении пространственных представлений;
− процесс преобразования этой информации в пространственный образ, полное представление о конструкции данного изделия, то есть осознание формы каждого элемента, понятие его величины и особенностей его строения, взаимосвязи между этими элементами, обусловлены размерами их взаимное расположение;
− процесс преобразования пространственного образа изделия в рабочий чертеж, содержащий двухмерные изображения изделия, его внутреннее устройство. Оптимизация изображений, создание такого документа, который содержит минимальное, но достаточное для производства и контроля изделия количество информации.
В инженерной деятельности процесс пространственного мышления реализуется в следующих случаях:
− при конструировании нового изделия, когда образ технического объекта, обладающего необходимыми свойствами и характеристиками, мысленно создается конструктором, воплощается в конкретную форму и выполняется в виде чертежного документа, содержащего изображения данного технического объекта;
− в технологической деятельности при изготовлении изделия, когда технолог по чертежу мысленно представляет форму и конструкцию изделия, разрабатывает технологический процесс его изготовления, включающий последовательно выполняемые операции: заготовительные, механической обработки, покрытия, термической обработки – в соответствии с требованиями конструкторской документации.
Пространственное воображение, создающее образ, присутствует на каждом из этих этапов, привносит в процесс эмоциональную составляющую, создает фантом, мысленную пространственную картину, позволяет рассмотреть этот пространственный образ разносторонне и включает процесс мышления, отбирающий необходимую для дальнейших действий информацию.
В данной публикации мы рассматриваем учебную деятельность при изучении графических дисциплин, в частности начертательной геометрии, и применение пространственного мышления при решении графических задач.
Например, рассмотрим задачи на определение натуральной величины плоского объекта общего положения, не параллельного и не перпендикулярного ни одной из плоскостей проекций.
На рисунке 1 изображен четырехугольник общего положения в двух проекциях, не параллельный и не перпендикулярный ни одной из плоскостей проекций.
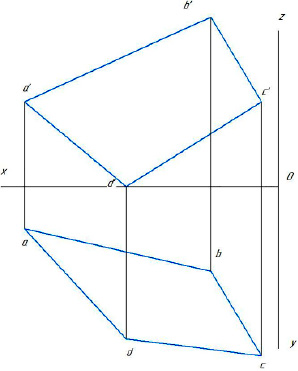
Рис. 1. Плоский четырехугольник общего положения
При ортогональном проецировании ни одна из проекций заданного плоского объекта не является его истинной формой, по которой можно определить размеры. Пространственное мышление преобразует информацию данного эпюра в следующий пространственный образ: угол d находится ниже всех остальных углов, но дальше от наблюдателя, чем угол c. Угол в выше всех углов и ближе к наблюдателю, чем угол а. Если представить комнату, в которой пол – это горизонтальная плоскость проекции, а стена, которая находится перед вами, – фронтальная плоскость проекции, то четырехугольник выглядит так: угол с – самый дальний от фронтальной стены, угол а находится ближе всех к фронтальной стене, по высоте эти углы расположены между углами d и b. Представим себе это расположение в конкретной комнате, и мы увидим четырехугольник, точнее, его пространственный образ, в своем воображении.
Чтобы при помощи методов начертательной геометрии построить его истинную величину, сначала развернем его так, чтобы он расположился перпендикулярно фронтальной стене, как это представлено на рисунке 2.
Для этого в плоскости четырехугольника проведена горизонталь, которая совпала с диагональю AC. Четырехугольник перемещен в новое положение, когда горизонталь (диагональ АС) расположена перпендикулярно фронтальной плоскости проекции, перемещение параллельно горизонтальной плоскости проекции, все углы четырехугольника остаются на той же высоте, но располагаются справа налево, уменьшая высоту. Самый высокий угол b расположен справа, самый низкий d – слева, углы a и c находятся на одной высоте и в одной точке фронтальной проекции. Таким способом фронтальная проекция четырехугольника преобразована в линию, и плоскость четырехугольника занимает фронтально-проецирующее положение.
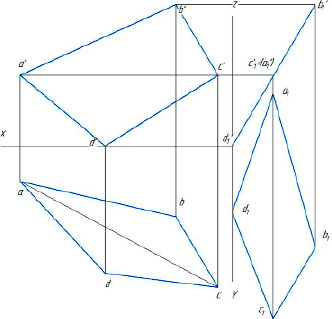
Рис. 2. Преобразование четырехугольника в проецирующую плоскость
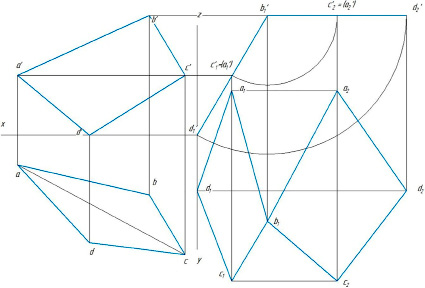
Рис. 3. Преобразование плоскости четырехугольника в горизонтальную плоскость уровня
Дальнейшим преобразованием чертежа при неизменных плоскостях проекций будет вращение четырехугольника относительно прямой линии, перпендикулярной фронтальной плоскости проекции, в новое расположение, параллельное горизонтальной плоскости проекции. Это преобразование изображено на рисунке 3. Задача решена, на горизонтальной плоскости проекции мы видим натуральную величину заданного четырехугольника.
Результаты исследования и их обсуждение
Как в этапах решения данной задачи присутствует пространственное мышление?
1. На начальном этапе необходимо создать образ заданного четырехугольника и мысленно определить его расположение относительно плоскостей проекций. Здесь нам помогает вышеприведенная аналогия с комнатой. Внесение реального объекта в решение задачи по начертательной геометрии позволяет материализовать образ плоскостей проекции и облегчает задачу создания образа четырехугольника. Выяснив факт общего расположения, не параллельного и не перпендикулярного ни одной из плоскостей проекций, и, следовательно, отсутствия в проекциях истинной величины плоской фигуры, переходим к следующему этапу преобразования чертежа.
2. Второй этап преобразования плоскости четырехугольника в проецирующую плоскость – это вспомогательное преобразование, мысленное перенесение заданного четырехугольника в новое положение при условии, что все точки перемещаются горизонтально и не меняют своей высоты. При этом ориентиром преобразования становится линия горизонталь, которая перемещается в новое положение, перпендикулярное фронтальной плоскости проекции, и при этом плоскость четырехугольника реформируется в плоскость, перпендикулярную фронтальной плоскости проекции.
3. Следующим этапом мы мысленно разворачиваем плоскость четырехугольника, перпендикулярную фронтальной плоскости проекции, в горизонтальное положение, параллельное горизонтальной плоскости проекции.
Введем в рассмотренную выше задачу материальный объект, взятый из жизненного опыта, например террасу на склоне горы в форме четырехугольника. Определить площадь террасы и ее форму – это актуальная задача землевладельца, которую можно решить при помощи методов начертательной геометрии. Здесь реализуется витагенно-ориентированный подход к решению задач [4], т.е. применение ситуаций жизненного опыта, активизирующих пространственное воображение иллюстрациями пространственных объектов из реального мира [5].
Первым этапом располагаем склон горы, на котором находится терраса, перпендикулярно плоскости проекции, т.е. наблюдатель становится перпендикулярно спуску горы, при этом видит проекцию террасы в виде прямой линии.
Вторым этапом склон вместе с террасой мысленно разворачиваем до горизонтального положения, в котором мы и видим истинную величину и форму террасы. Описывая построение с применением объектов материального мира, мы используем пространственное воображение для создания образов геометрических объектов и стимулируем пространственное мышление обучаемых [6].
Выводы
Таким образом, в результате рассмотрения процесса решения задачи по начертательной геометрии, анализа этапов ее решения с точки зрения применения пространственного мышления было установлено, что:
− на разных этапах решения задачи возникает необходимость преобразования плоских изображений эпюра (чертежа) в пространственные объекты при помощи пространственного воображения;
− решение рассмотренной задачи невозможно без использования пространственного мышления, способствующего преобразованию объектов, расположенных под углами к плоскостям проекций, и, таким образом, не выявляющих на проекциях их настоящую величину и форму, в положение частное: перпендикулярное либо параллельное плоскостям проекция;
− применение в процессе решения задачи объектов материального мира, условно образов жизненного опыта, реализующих витагенно-ориентированный подход к решению задачи, активизирует пространственное воображение обучаемых;
− замена абстрактных объектов реальными предметами материального мира стимулирует пространственное мышление и наполняет задание реальным содержанием, которое включает решение практико-ориентированных проблем.
Библиографическая ссылка
Туркина Л.В. ВИТАГЕННО-ОРИЕНТИРОВАННЫЙ ПОДХОД В РАЗВИТИИ ПРОСТРАНСТВЕННОГО МЫШЛЕНИЯ ПРИ ИЗУЧЕНИИ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ // Международный журнал экспериментального образования. 2023. № 3. С. 32-37;URL: https://expeducation.ru/ru/article/view?id=12148 (дата обращения: 12.02.2026).
DOI: https://doi.org/10.17513/mjeo.12148

