Введение
Известно, что в прошлом, когда геометрия была более развитой, чем алгебра, математические задачи решались с помощью геометрических методов. Однако в настоящее время многие люди не проявляют интереса к этой науке, возможно, потому что они не осознают её важность в повседневной жизни и не представляют, как она может быть полезна в их будущей профессиональной деятельности. Поэтому, чтобы сделать геометрию более понятной и увлекательной, можно использовать номограммы и современные компьютерные технологии [1]. На уроках геометрии ученики знакомятся с таблицей В. М. Брадиса, умение работать с которой открывает новые возможности. В приложении к таблице имеются два рисунка, которые помогают решать приведенные квадратные уравнения и уравнения вида
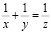– это номограммы [2, с.82-84].
Существует метод, который позволяет создавать специальные инструменты для каждой формулы. Эти инструменты освобождают обучающихся от сложных вычислений и сразу дают нужный результат. Такие инструменты называются номограммами, а наука, изучающая их построение, – номографией.
Графическая интерпретация функции, зависящей от множества параметров, называется номограммой (по-гречески «номос» означает закон). Используя базовые геометрические методы, например, применение линейной шкалы, возможно изучение зависимостей между величинами без необходимости в сложных расчетах. Например, можно находить корни квадратных уравнений без применения специальных формул.
Цель исследования изучить, как номограммы могут быть полезны в изучении курса геометрии, и создать их с помощью современных компьютерных технологий.
Материалы и методы исследования
В процессе написания статьи авторами был проведён глубокий анализ научно-методической литературы, посвящённой номограммам. Изучены их история возникновения, классификация и особенности применения в курсе геометрии и других прикладных дисциплинах. С помощью интерактивной геометрической системы «Живая геометрия» были построены различные номограммы, а также продемонстрировано их практическое использование.
Результаты исследования и их обсуждение
Изображения геометрических связей между параметрами, облегчающие расчеты, существуют уже давно. Эти конструкции включают в себя группы линий и градуировок, применяемых, например, в солнечных приборах времени и астрономических инструментах. Создание концепции графических изображений началось в девятнадцатом столетии. Французский специалист по строительству Л.К. Лаланн разработал концепцию создания линейных решетчатых номограмм в 1843 году. Основополагающие принципы номографического проектирования были разработаны М. д’Оканем в период между 1884 и 1891 годами. В России изучением номографических методов впервые занялся Н.М. Герсеванов в период между 1906 и 1908 годами. Н.А. Глаголев внес значительный вклад в развитие теоретических основ номографии и структурирование процесса графического представления инженерных вычислений. Хотя номография представляет собой сравнительно новое направление, установить точную дату её появления довольно сложно. Логарифмическая шкала Гунтера фактически уже представляла собой номограмму. Впервые полноценная номограмма в точном значении этого термина была представлена в книге Ж. Пуше «Линейная арифметика» в 1795 году для выполнения операции умножения.
Номограммы отличаются друг от друга методами отображения данных параметров (через точки или линии) и методами сопоставления изображений переменных. Наиболее часто встречаются такие типы номограмм, как транспарантные, сетчатые и составленные из выровненных точек.
1. Транспарантные номограммы
В самом элементарном варианте номограмма включает две поверхности: главную поверхность и прозрачный лист с картинками параметров. Часто транспарант создаётся из прозрачного материла. Примером транспарантной номограммы является логарифмическая линейка.
2. Сетчатые номограммы
Для создания сетчатых номограмм из прямых линий используются функциональные сетки, наиболее элементарными среди которых являются логарифмические и полулогарифмические. Помимо прямой линии, также используются и другие, известные как разрешающие показатели диаграммы: круги (по Годселю), произвольные кривые (по Швердту), ребра чертежных угольников (по Сиглеру) и т.д. Используя сетчатые диаграммы, возможно изучение связей между корнями квадратичного уравнения.
3. Номограммы из выровненных точек
Для уравнений с тремя неизвестными используются три шкалы, разработанные таким образом, чтобы три точки, соответствующие уравнению, располагались на одной линии – именно поэтому такой тип диаграммы имеет такое название. Номограммы из выровненных точек положили начало развитию номографии – области математики, которая сочетает теоретические основы и практические подходы к созданию номограмм.
Большинство номограмм можно создать с использованием программного обеспечения интерактивной геометрии: модуля «Живая геометрия», который является частью учебного комплекса «1С:Математика, 5-11 классы». Практический курс, созданный в рамках программы «Цифровизация образовательной системы».
«Живая геометрия» – это программное обеспечение для работы с геометрическими чертежами (цифровая математическая мастерская), предоставляющее возможность создавать корректируемые рисунки, а также выполнять все требуемые измерения. Программа позволяет не только находить закономерности в геометрических явлениях, но и формулировать и подтверждать доказанные теоремы. Она развивает логическое мышление, пространственное воображение, обеспечивая фундамент для проектной деятельности обучающихся [3, 4].
Рассмотрим некоторые примеры построения номограмм с помощью программы «Живая геометрия».
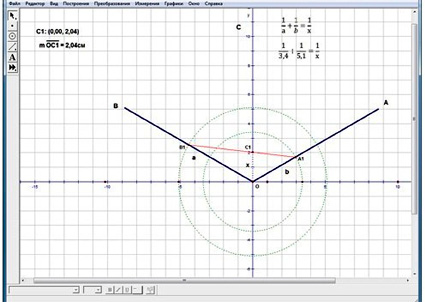
Рис.1. Номограмма уравнения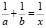 
Пример 1. Найти решение уравнения вида:
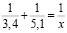
Построим номограмму для решения уравнения такого вида (рис.1). Угол АОВ=1200, ОС – биссектриса этого угла. На стороне ОВ отложим отрезок ОВ1 = 5,1, а на стороне ОА – отрезок ОА1 = 3,4. Отрезок, соединяющий точки А1В1, пересечет биссектрису ОС в точке С1. Длина отрезка ОС1 и будет решением уравнения. Измерим ее с помощью меню Измерения – Длина. Получим х = 2,04. Точность результата в программе можно установить до пяти знаков после запятой.
Пример 2. Найти решение уравнение вида
.
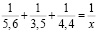Так как номограмма уравнения
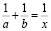
является частью рассматриваемой номограммы [5], в программе «Живая геометрия» создадим новый инструмент Номограмма 1 и сделаем чертеж. Для этого в номограмме внесем некоторые дополнения: продолжим одну из сторон угла за вершину О, например, сторону АЕ. Эта номограмма является соединением двух номограмм предыдущего примера.
На прямой ОА найдем точку А1 с пометкой 5,6, на прямой ОС – точку С1 с пометкой 3,5, соединим их прямой А1С1. Она пересечет ОВ в точке В1, пометка d1 удовлетворяет уравнению:
.
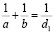Заменяя в уравнении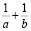 
через 
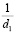, получим уравнение
.
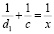Далее на прямой ОD находим точку D1 c пометкой 4,4 = с. Соединим D1 c В1. Длина отрезка АЕ будет решением уравнения. Замерим ее с помощью инструмента Длина. Получим х = 1,45 (рис.2).
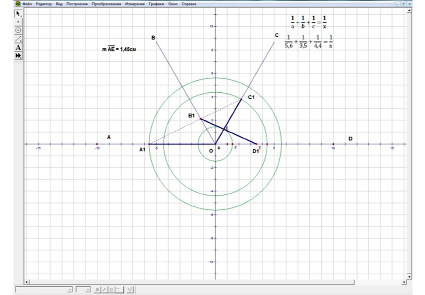
Рис. 2. Номограмма уравнения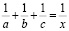 
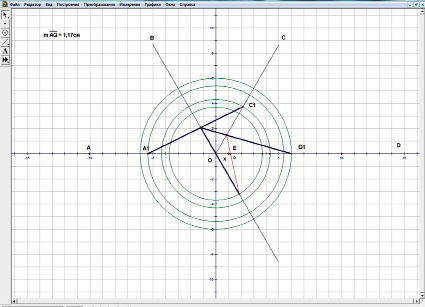
Рис. 3. Номограмма уравнения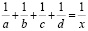 
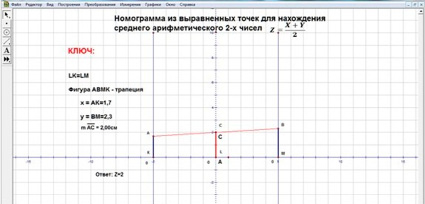
Рис. 4. Номограмма для нахождения среднего арифметического двух чисел
Пример 3. Найти решение уравнения
.
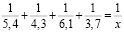Для построения номограммы уравнения
,
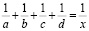воспользуемся предыдущей номограммой, сделав в ней некоторые дополнения: продолжим сторону ОВ за вершину О. Эта номограмма является соединением трех номограмм примера 1 (рис.3). Длина отрезка AQ и будет решением уравнения. Получим х = 1,17.
Пример 4. Найти среднее арифметическое двух чисел
Пусть x = 1,7 и y = 2,3. Проведем две параллельные линии относительно оси Оу на одинаковом расстоянии от начала координат. На одной из них отложим расстояние равное 1,7, на другой – 2,3, соединим полученные точки (рис.4). Полученная фигура – трапеция. Искомая величина – средняя линия трапеции. Измерим отрезок АС с помощью инструмента Длина. АС = 2.
Используя программу «Живая геометрия» для построения номограмм, можно легко изменять исходные данные и быстро получать результат. Использование каждой номограммы для нахождения по ней решения необходимо обосновывать.
К уравнению вида
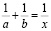
приходится часто прибегать при решении задач физики. В разделе «Оптика» для определения фокусной длины тонкого объектива. В разделе «Электричество» для определения суммарного сопротивления при одновременном подключении проводящих элементов; для расчета совокупной емкости схемы, включающей два последовательных конденсатора; для определения совокупной индукции схемы, содержащей две катушки при их параллельном соединении [6].
Номограммы являются эффективным инструментом для ускорения вычислений. Использование номограмм на уроках геометрии способствует повышению интереса обучающихся к предмету и пониманию его практического применения. В процессе обучения математике номограммы помогают обучающимся установить связь между геометрией, алгеброй, физикой, информатикой. Они формируют умения работы с чертежом, устанавливают взаимосвязь между теоретическими знаниями и практическими навыками, развивают пространственное воображение, логическое мышление обучающихся [7, 8].
Заключение
Разработка и создание номограмм представляет собой искусство, требующее глубоких знаний и навыков. В математике существует отдельный раздел, посвящённый этому процессу.
Для создания номограммы необходимо не только грамотно спланировать маршрут по данным, но и выбрать масштаб, который будет охватывать весь необходимый диапазон информации.
Недостатком номограммы является то, что она пригодна только для той формулы, для которой построена. Несмотря на это, простота использования, достаточно высокая точность результата, наглядность обеспечивает широкое их применение в различных областях.
Частое применение номограмм наблюдается в прикладных областях знаний, так как математики и теоретики-физики обычно располагают теоретическими или экспериментальными соотношениями, и им, как правило, необходимо получить точные решения заданных уравнений. Вместе с тем, медицинским специалистам, метеорологам, архитекторам, инженерам и разработчикам обычно не нужно стремиться к экстремально высокой точности, поскольку достаточно иметь одну-две значимые цифры. Их диаграммы составляются преимущественно не на основе математических уравнений, а на основании данных предварительных исследований. Существуют многочисленные случаи применения номограмм: при вычислении параметров противопожарных установок, силы нажима и эффективности газовых факелов, в роли инструментов ориентации и контроля полета, для определения силы землетрясения и обработки данных статистического анализа сейсмических угроз и т.д.
Библиографическая ссылка
Нагодкина М.Н., Ячинова С.Н. СЧИТАЮЩИЕ ЧЕРТЕЖИ В ОБУЧЕНИИ ГЕОМЕТРИИ // Международный журнал экспериментального образования. 2024. № 4. С. 39-44;URL: https://expeducation.ru/ru/article/view?id=12189 (дата обращения: 04.07.2025).
DOI: https://doi.org/10.17513/mjeo.12189