В общем случае краевая задача состоит из основных уравнений теории упругости, уравнений движения вязкой жидкости, уравнений неразрывности и граничных условий.
Уравнение движения упругого слоя имеет вид:
(1)
(2)
Уравнение движения вязкой жидкости и неразрывности:
,
=0 (3)
Граничные условия будут иметь вид:
при 
(4)
где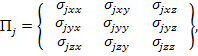 
j=1,2 (5)
при 
(6)
при z=h 
По времени и по горизонтальным координатам ставятся условия периодичности:
T
Здесь 
- вектор скорости вязкой жидкости, 
- вектор деформаций в упругом слое, 
- объемная сила, E - модуль Юнга, G=const-модуль сдвига, σ -коэффициент Пуассона, ρ1 - плотность материала упругого слоя, ρ2 - плотность вязкой жидкости, П1 -тензор напряжений в упругом слое, П2 - тензор напряжений в вязкой жидкости, μ - коэффициент динамической вязкости жидкости, v- коэффициент кинематической вязкости жидкости, L - длина свободных волн, K - их волновое число, T - период колебаний, ω - их частота.
, 
(7)
, 
(8)
, 
(9)
, 
(10)
, 
(11)
, 
(12)
Предположим что выполняются следующие условия:
, 
vx≡0, vz≡0, 
,vy =v(x,z,t) (13)
Таким образом, предположим, что смещение верхней границы упругого слоя производится в направление оси Oy при отсутствии смещений в других направлениях.
Это - постановка задачи для антиплоских колебаний упругого слоя, лежащего на поверхности вязкой жидкости.
Построим решение для жидкости в виде бегущих волн:
(14)
Убывающее на -∞ решение этого уравнения имеет вид:
,Re 
(15)
Далее построим решение для антиплоских колебаний упругого слоя
Первое и третье уравнение системы (1) удовлетворяются тождественно, а второе уравнение и соответствующие ему граничные условия примут следующий вид:
(16)
z=0, 
,
(17)
Решение для u ищем в виде: 
Имеем:
(18)
Из нулевых граничных условий 
при z=H находим, что B=0. Далее из (22), (23) получается следующее система уравнений:
C=0; 
(19)
Определитель этой системы дает частотное уравнение:
(20)
Его корни находятся асимптотически и численно. Асимптотики построены для случаев: K1>>1, K1<<1 при с помощью итерационных процессов. В окрестности Ω = χ построены другие асимптотические разложения.
Тем самым найдены частоты свободных антиплоских колебаний системы упругий слой - вязкая жидкость.
Библиографическая ссылка
Золотарев А.А., Кандалфт Х., Потетюнко Э.Н. ЗАДАЧА О СВОБОДНЫХ АНТИПЛОСКИХ КОЛЕБАНИЯХ СИСТЕМЫ УПРУГИЙ СЛОЙ - ВЯЗКАЯ ЖИДКОСТЬ // Международный журнал экспериментального образования. – 2010. – № 1. – С. 41-43;URL: https://expeducation.ru/ru/article/view?id=245 (дата обращения: 03.12.2024).