В данной работе предлагается метод обработки для подавления помех синусоидального типа. Нелинейная обработка осуществляется на огибающей и использует адаптивное квантование. В качестве критерия адаптации выбран критерий минимума среднего квадрата отклонения квадратур сигнала на выходе антенной решётки (АР).
Считаем, что сигнал, принятый k-ым приёмным элементом АР в момент времени ti, представляет собой аддитивную смесь полезного сигнала sik, синусоидальной помехи xik и гауссовского шума vik. Считаем также, что при дискретизации условия теоремы Котельникова выполняются.
В качестве помехи выбираем синусоидальное колебание с постоянной амплитудой Ax и угловой модуляцией φxi:
где t*- пространственная частота визирования; tx - пространственная частота помехи; ω0 - центральная частота спектра помехи.
Квадратурные составляющие помехи в дискретные моменты времени в k - ом элементе АР:
и 
В качестве полезного используем гармонический сигнал с постоянной амплитудой As , угловой модуляцией φsi и случайной начальной фазой φs0, равновероятной на интервале (0,2π):
и 
,
где ts - пространственная частота полезного сигнала.
Период изменения фазы сигнала и период изменения фазы помехи различны.
Считаем, что отсчёты квадратур шума vi распределены по нормальному закону с нулевым математическим ожиданием и единичной дисперсией. Тогда огибающая помехи распределена по закону Райса с параметром 
.
Структурная схема обработки для обнаружения сигнала с неизвестной начальной фазой представлена на рис.1. и содержит АР (пространственную обработку) и коррелятор (временную обработку).
Принятый сигнал после умножения квадратур отклика АР на соответствующие квадратуры опорного сигнала может быть представлен в виде:
;
; (1)
Значение пространственного спектра на выходе АР в направлении Θ можно представить следующим образом: 
, где UΘj- значение спектра на выходе АР в направлении Θ для j - ой реализации, а Θ меняется от -900 до 900.
Для оптимального приема слабых сигналов на фоне узкополосных помех с негауссовым распределением мгновенных значений вероятностей используют нелинейное преобразование g(A) огибающей смеси сигнала и помехи [1]:
где W(A)- плотность вероятности огибающей помехи, c ≠ 0 - произвольная константа.
При меняющихся характеристиках помехи преобразование должно быть адаптивным. На выходе устройства обработки, в результате нелинейного преобразования огибающей g(Ai), получим преобразованные квадратуры:
(2)
Считаем, что наилучшим преобразованием огибающей будет преобразование, обеспечивающее минимум среднего квадрата ошибки воспроизведения квадратур сигнала на выходе первого и второго канала соответственно:
,
(3)
где c ≠ 0; N=T/Δt - количество отсчетов, взятых для адаптации.
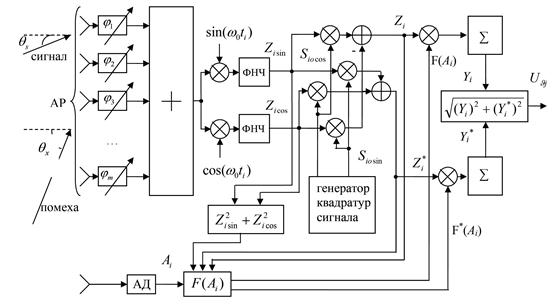
Рис. 1. Структура АР с нелинейной обработкой сигнала с неизвестной случайной фазой
Представим амплитудную характеристику нелинейного преобразователя огибающей в виде
,
тогда
. (4)
Здесь hk - параметры настройки нелинейного преобразователя;
(5)
- система взаимно-ортогональных функций; k = 1,2,...,m.
Генератором такой системы функций служит обычный аналого-цифровой преобразователь, осуществляющий квантование на m уровней и дискретизацию во времени [3]. Далее считаем m=256.
Подставим F(Ai) в (3) и найдём оптимальные параметры настройки преобразования, обеспечивающие минимум ошибки (3) для первого и второго каналов соответственно:
,
.
В табл. 1. приведены значения выигрыша μ, дБ в отношении сигнал-помеха нелинейной обработки по сравнению с линейной для мешающего воздействия на АР в виде одной и пяти помех в зависимости от параметра α и отношения сигнал-помеха q на входе.
Таблица 1
|
q, дБ |
α, дБ |
|||||
|
Одна помеха |
Пять помех |
|||||
|
0 |
10 |
20 |
0 |
10 |
20 |
|
|
-10 |
8.29 |
9.96 |
7.46 |
4.29 |
1.32 |
-0.02 |
|
-20 |
16.55 |
21.81 |
20.74 |
12.1 |
12.61 |
7.67 |
|
-30 |
18.33 |
22.32 |
27.56 |
13.82 |
15.35 |
15.61 |
Результаты исследования показали, что:
- нелинейную обработку целесообразно проводить для слабых сигналов (q << 1) и чем слабее сигнал, тем больше выигрыш от применения нелинейной обработки по сравнению с линейной АР;
- эффективность нелинейной обработки возрастает с увеличением параметра распределения синусоидальной помехи α (степени негауссовости);
- применение данной обработки позволяет существенно (до 27 дБ) улучшить отношение сигнал/помеха на выходе АР.
СПИСОК ЛИТЕРАТУРЫ
- Теория обнаружения сигналов / П.С.Акимов [и др.]; под ред. П.А.Бакута. М.: Радио и связь, 1984. 440 с.
- Валеев В.Г. Помехоустойчивая цифровая обработка многоканальных сигналов / В.Г. Валеев, А.А. Язовский // Известия Академии наук. Теория и системы управления. 1996, №6. С. 84- 87.
- Валеев В.Г. Амплитудные нелинейные фильтры с квантованием сигналов для подавления негауссовских помех / В.Г. Валеев, А.Г. Долматов, А.А.Язовский // Радиотехника и электроника. 1991. Т. 36. № 2. С. 352 - 357.
Библиографическая ссылка
Королева С.С., Язовский А.А. АДАПТИВНАЯ НЕЛИНЕЙНАЯ ОБРАБОТКА СИГНАЛА СО СЛУЧАЙНОЙ НАЧАЛЬНОЙ ФАЗОЙ ПРИ СИНУСОИДАЛЬНЫХ ПОМЕХАХ В АНТЕННОЙ РЕШЁТКЕ // Международный журнал экспериментального образования. – 2010. – № 1. – С. 87-90;URL: https://expeducation.ru/ru/article/view?id=277 (дата обращения: 21.11.2024).