Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Дасибеков А. 1 Юнусов А.А. 1 Юнусова А.А. 2

---

1 Южно-казахстанский государственный университет имени М. Ауэзова

2 Казахская академия транспорта и коммуникации имени М. Тынышпаева

В данной работе приведена различная постановка упругих и упругоползучих задач уплотнения глинистых грунтовых оснований с устройством песчаной подушки, обладающих неоднородным свойством. Причем неоднородность земляных масс выражается через их модуль деформации. То, что грунт по своей структуре является неоднородным строительным материалом, это уже доказано. Однако, как математически описать неоднородность уплотняемого грунтового массива, это уже вопрос? Профессор Г.К. Клейн проводя расчет осадок сооружений неоднородного линейно-деформируемого полупространства модуль его деформации считает переменным по степенному закону глубины уплотняемого массива. В то же время Г.Я. Попов, изучая изгиб плит на упругом неоднородном полупространстве, его модуль деформации считает переменным по экспоненциальному закону глубины. Причем каждый убедительно доказывает, что неоднородность грунта можно учесть, только так. Основываясь на эти работы, нами для изучения процесса упругих и упругоползучих задач консолидации водонасыщенных неоднородных грунтов, их модуль деформации также считается переменным по глубине. Свойство ползучести грунтов при этом учитывается через теорию Г.Н. Маслова, Н.Х. Арутюняна. Кроме того, в данной работе учитывается структурная прочность сжатия грунта. часть нагрузки, равная величине сразу же воспринимается скелетом грунта. В качестве примера приведены решения задач уплотнения упругих и упругоползучих задач уплотнения глинистых грунтовых оснований, модуль деформации, которых изменяется по экспоненциальному закону глубины.

Статья в формате PDF

1049 KB

оснований песчаной подушки

грунт

деформация. фундамент

неоднородност

зависимость. сжимаемость

упругих и упругоползучих грунтов

1. Абелев М.Ю. Строительство промышленных и гражданских сооружений на слабых водонасыщенных грунтах. – М.: Стройиздат, 1983. – 247 с.

2. Арутюнян Н.Х. Некоторые вопросы теории ползучести. – М.: Гостехтеориздат, 1952. – 323 с.

3. Баршевский Б.Н. Одномерная задача консолидации для грунтов с переменным по глубине модулем деформации // Некоторые вопросы машиностроения и строительной механики: сб. – Л., 1967. – Вып. 68. – Ч.1. – С. 55–61.

4. Бердыбаева М.Ж., Дасибеков А.Д., Ахметов Д.А., Ахметов А.Р. Об уплотнении наследственно-стареющих неоднородных грунтов с неоднородными граничными условиями // Вестник НИИстройпроекта. – Алматы, 2006. – № 1–2 (8). – С. 65–72.

5. Месчян С.Р. Экспериментальная реология глинистых грунтов. – М.: Недра, 1985. – 342 с.

6. Клейн Г.К. Расчет осадок сооружений по теории неоднородного линейно-деформируемого полупространства // Гидротехническое строительство. – 1948. – № 2.– С. 7–14.

7. Попов Г.Я. К теории изгиба плит на упругом неоднородном полупространстве //Строительство и архитектура. – 1959. – № 12. – С. 11–19.

8. Флорин В.А. Основы механики грунтов. – М.: Госстройиздат, 1961. – т.2. – С. 60–276.

9. Ширинкулов Т.Ш., Дасибеков А.Д., Бердыбаева М.Ж. Двумерное уплотнение упругоползучих грунтов при неоднородных их граничных условиях //Механика и моделирование технологических процессов. – Тараз, 2006. – № 1. – С. 61–66.

Строительство сооружений на слабых водонасыщенных глинистых грунтах требует более внимательного подхода к ним. Это связано с тем, что сооружения, взаимодействующие с такими грунтами, испытывают большие осадки. Если залегающие непосредственно под подошвой фундамента грунты слабые, рыхлые, с малым расчетным сопротивлением, то прежде чем строить высотные здания создают искусственные основания. В этом случае в качестве основания применяются песчаные подушки мощностью от 1–2 до 7 м. Слабые грунты под подошвой удаляют на глубину, определяемую расчетом, а образовавшийся котлован заполняют песком разного калибра или гравием, обладающим малой сжимаемостью и допускающим сильное давление. Следовательно, при закладке фундамента существенную роль выполняет песчаная насыпная подушка, и использования песчаной подушки при сооружении фундамента может дать существенную экономию материальных средств. Именно песчаная подушка способна стать действенным способом, с помощью которого удается создать оптимальную нагрузку на нижнюю часть фундамента. Благодаря песчаной подушке, можно выполнить поднятие нижней части фундамента относительно уровня грунтовых вод, а также добиться полного исключения соприкосновения фундамента со строительными объектами и материалами, являющегося причинами деформаций. Основания, во время выполнения которых использовалась песчаная подушка под фундамент, выделяются повышенной стойкостью к возможным перепадам температур, давлению и уровню влагостояния в почве. Короче говоря, они позволяют уменьшить глубину заложения фундаментов и увеличивают их устойчивость, а также применение их уменьшает осадки фундаментов. Кроме того, песчаные подушки используются в качестве дренирующего слоя, так как поровая вода из нижележащих водонасыщенных глинистых грунтов отжимается в процессе уплотнения грунтов от веса самой подушки, ускоряя процесс консолидации грунтов основания.

На тех основаниях, где имеется высокий уровень грунтовых вод, укладку подушки делают только с предварительно созданным дренажем. Поскольку такие грунты могут вспучиваться и промерзать, представляя тем самым потенциальную опасность для фундамента. Иногда для возведения фундаментной подушки песок не используется. Его можно заменить, к примеру, гравием, в который входит песчаная фракция. Этот материал так же хорошо будет сдерживать нагрузки со стороны фундамента. Технология его укладки практически ни чем не отличается от укладки песка. Кстати, и сам фундамент на гравийной подушке будет стоять долго. Это достаточно надежное основание. Щебень так же является хорошим заменителем песка, его обычно используют в проблемных грунтах, на которых фундамент заливать сложно. Но все, же специалисты рекомендуют даже щебень смешивать с песком. Он просто заполнит все пространство, которое остается между частями фракции. Песчаные и щебеночные (или гравийные) подушки предназначены для распределения давления от фундамента на большую площадь либо для замены слоя слабого грунта под фундаментом.

Кроме того, деформативные свойства грунтов, вообще говоря, меняются с координатами точки, и допущение об их однородности представляет собой идеализации реальных состояний уплотняемых земляных масс. В этом отношении теоретические и экспериментальные исследования Г.К. Клейна [6], Попова Г.Я. [7], Б.Н. Баршевского [3] и других исследователей показали, что грунты, на которых строятся сооружения, по своим механическим свойствам являются неоднородными и эта неоднородность грунта может изменяться по глубине согласно законам

(1)

(2)

где Em является модулем деформации грунта на глубине z = 1; показатель m в большинстве случаев лежит в пределах 0 < m < 2; E0, α – опытные данные.

Как известно, что грунт – это минерально-дисперсное тело и обладает определенной пористостью. Изменения пористости под влиянием внешних нагрузок от сооружения подчиняются следующим закономерностям: во-первых, изменению коэффициента пористости от давления, сдвигу при трении и скольжения; ламинарной фильтрации; во-вторых, линейной или нелинейной деформируемости. Здесь при оценке сжимаемости грунтов важно выяснить зависимость между изменениями внешней нагрузки и изменением коэффициента пористости грунтов. Если неоднородная грунтовая среда обладает свойством нелинейной ползучести, то зависимость между коэффициентом пористости и суммой главных напряжений, согласно [8], имеет вид

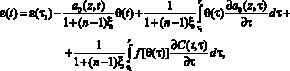(3)

где (4)

ε(t), θ(t) – эти функции также изменяются по координатам x, y, z; f[θ(τ)] – функция, характеризующая нелинейную зависимость между коэффициентом пористости и суммой главных напряжений в скелете грунта; φ(τ) – функция старения; a1, γ1 – параметры ползучести; τ1t1 – момент приложения внешней нагрузки; x – коэффициент бокового давления; а0 – коэффициент сжимаемости грунта, который в общем виде может зависеть от глубины исследуемой точки и времени уплотняемого массива; п – размерность рассматриваемой задачи; C(t, τ) – мера ползучести.

Причем функция f[θ(τ)] может изменяться в виде

(5)

Зависимость (5) при n = 1 и (3), т.е. для одномерной задачи теории уплотнения впервые была применена В.А. Флориным [9]. Он теорию упругоползучего тела Г.Н. Маслова-Н.Х. Арутюняна [2] смог применить к описанию процесса уплотнения однородных глинистых грунтов, обладающих свойством ползучести. Причем экспериментальные исследования С.Р. Месчяна [5] доказали применимость этой теории к водонасыщенным глинистым грунтам.

Для линейной задачи теории механики уплотняемых пористых упругоползучих неоднородных грунтов зависимость (3) переходит к следующему виду

(6)

где функция δ(t, τ), входящая в (6), находится из следующего выражения

(7)

Функция φ(τ), входящая в (7), обычно представляется в виде

(8)

Заметим, что кроме (8) встречаются и другие меры ползучести, предложенные И.Е. Прокоповичем и И.И. Улицким, С.Е. Александровским, С.Р. Месчяном и др.

Эти зависимости, т.е. (3)–(8) будут описывать состояния скелета слабых глинистых неоднородных упругоползучих грунтов, находящихся под давлением тех или иных внешних нагрузок. Для уплотнения неоднородных грунтовых оснований, обладающих только упругим свойством выражения (3), (6) имеют вид:

(9)

Далее, чтобы решить те или иные задачи механики уплотняемых пористых двухфазных сред необходимо совместно рассматривать уравнение, отражающее условие неразрывности жидкой и твердой фаз грунта

(10)

где kx, ky, kz – соответственно, коэффициенты фильтрации грунта в вертикальном и горизонтальном направлениях; εср– среднее значение коэффициента пористости в процессе уплотнения; γв – объемный вес воды; t – время уплотнения грунтового массива. Причём здесь, когда α2 = 1, α3 = 1, α1 = 0, задача соответствует трёхмерному уплотнению; когда α3 = 0, α2 = 1, α1 = 0, задача соответствует двумерному уплотнению, когда α1 = 0, α2 = 0, α3 = 0, задача соответствует одномерному сжатию; когда α1 = 1, α2 = 1, α3 = 0, исследуется осесимметричная задача уплотнения.

Уравнение состояния его скелета

(11)

Здесь ε(M, t)– изменяющийся во времени коэффициент пористости; θ(M, t)– сумма главных напряжений; x – коэффициент бокового давления; ε(M, t)– изменяющийся во времени коэффициент пористости.

А также условия равновесия уплотняемого грунтового массива

(12)

где p(M, t)– давление в поровой жидкости; М(x, y, z) – исследуемая точка уплотняемого массива; x, y, z – координаты точки в пространстве; θ*(M) – сумма главных напряжений для стабилизированного состояния грунта; p*(M) – поровое давление для этого же состояния.

Следует заметить, что равенство (10) включает в себе условия неразрывности жидкой и твердой фаз грунта, а также закон фильтрации. Однако оно еще не дает возможности определить распределение давлений в поровой жидкости, тем более нельзя что-либо говорить о напряженно-деформированном состоянии уплотняемого грунтового массива. Для решения этого вопроса заранее должна быть установлена математическая модель, которая с достаточной точностью может описать состояния самого скелета грунта. Если грунтовая среда обладает упругим свойством, то зависимость (11) между коэффициентом пористости и суммой главных напряжений имеет вид (9). При упругоползучей среде состояние уплотняемого грунтового массива описывается выражениями (3) или (6) в зависимости от линейного или нелинейного деформирования скелета грунта. Некоторые результаты таких задач в различных постановках получены в работах [4, 9]. Если рассмотрим совместно соотношения (9), (10) и (12), то одномерное уравнение консолидации неоднородных грунтов, обладающих упругим свойством, приводится к виду:

(13)

где : q(z,t) – распределенная нагрузка. Здесь неоднородность уплотняемого грунта математически представлена в виде Если неоднородность грунта имеет вид (2), то уравнение (13) представляется так:

(14)

Начальное условие для уравнений (13) и (14) запишем в виде [1]:

(15)

т.е. часть нагрузки, равная величине структурной прочности сжатия Pстр, сразу же воспринимается скелетом грунта.

Выражения (13) и (14) для уплотняемой линейной упругоползучей среды соответственно имеют вид

(16)

(17)

Начальными условиями для этого уравнения будут (15) и

(18)

(19)

В целом математическая постановка задач (13)–(19) заключается в следующем. Требуется определить давление в поровой жидкости p(z, t), напряжение в скелете грунта σ(z, t) и вертикальные перемещения точек верхней поверхности s(t) (осадок) слоя уплотняемого грунта.

Ниже рассмотрим случай, когда на слой неоднородного водонасыщенного грунта мощностью h, залегающего под песчаной подушкой, обладающего упругим свойством в начальный момент времени (t = τ1) мгновенно прикладывается равномерно распределенная нагрузка с интенсивностью q. Если неоднородность грунта подчиняется выражению (2), то исследование этой задачи сводится к решению уравнения (19) при (15) начальном условии. Причем граничные условия имеют вид:

(20)

В (20) первое начальное условие имеет место за счет песчаной подушки, а второе граничное условие относится к глубине h, ниже которой фильтрации не происходит.

Решение уравнения (14) при начальном (15) и граничных (20) условиях, относительно давления в поровой жидкости, получится в виде:

. (21)

Здесь

(22)

(23)

J0, Y0 – функции Бесселя 1-го и 2-го родов нулевого порядка, которые имеют вид:

Причем, применяя признак Даламбера, легко установить, что J0 и Y0 сходятся равномерно при всех х.

Параметр , входящий в выражения (21)–(23) находится из следующего равенства:

(24)

В связи с тем, что решение данной задачи приводит к нахождению числовых значений бесселевых функций нулевого порядка, то определение порового давления (21) можно считать доведенным до конца, так как для функций Бесселя составлены обширные таблицы.

Напряжение в скелете неоднородного грунта находятся из следующей расчетной формулы

(25)

Полученные выражения (21) и (25) соответственно позволяют определить изменения давления в поровой жидкости и напряжений в скелете грунта для любой точки рассматриваемой конечной области уплотнения неоднородного двухфазного грунта, обладающего упругим свойством. После того как определено напряжение в скелете уплотняемого неоднородного грунтового массива, можно вычислить и вертикальные перемещения точек верхней поверхности уплотняемого слоя грунта (осадок). Действительно, если к поверхности слоя грунта приложена некая вертикальная нагрузка, то соответствующая ей осадки s(t), может быть определены по формуле [8], т.е.

(26)

Теперь рассмотрим случай, когда уплотняемая неоднородная грунтовая среда обладает упругоползучим свойством. Тогда необходимо решать краевую задачу (17), (15), (19), (20). Её решение относительно порового давления представим в виде:

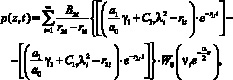(27)

где

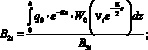
r1i, r2i – решение следующего уравнения

 – находится из выраже-
ния (22).

Напряжение в скелете водонасыщенного глинистого неоднородного грунта вычисляется по формуле

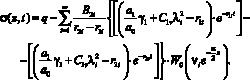(28)

Определим теперь осадку слоя неоднородного водонасыщенного глинистого грунта по формуле (26), т.е.

(29)

где

Из (29) при t → ∞ имеем

Пользуясь расчетными формулами (27)–(29), вычислены давления в поровой жидкости, напряжения в скелете грунта и вертикальные перемещения точек верхней поверхности неоднородного уплотняемого водонасыщенного глинистого грунтового основания, обладающего упругоползучим свойством. Эти результаты дали возможность также исследовать уплотнение неоднородного упругоползучего слоя грунта под действием нагрузки, линейно возрастающей по глубине; уплотнение неоднородного упругоползучего слоя грунта под действием нагрузки, убывающей по глубине; уплотнение грунтового основания, расположенного между фильтрующими слоями.

Библиографическая ссылка