Курс «Математический анализ» студенты изучают на 1-2 курсах педагогических университетов, а в дальнейшем используют полученные знания в течение всего обучения в университете (комплексный анализ, дифференциальные уравнения, уравнения математической физики, педагогическая практика), а также в педагогической деятельности. В первые годы обучения в университете большинство студентов мало внимания уделяют будущей профессии. В то же время материал курса «Математический анализ» имеет мощный потенциал для систематического формирования у студентов готовности к педагогической деятельности. Например, если на лекции студентам демонстрируют приемы решения не только теоретических, но и прикладных задач, то у них расширяется математический кругозор и создаются образцы для наследования. Для физиков, инженеров, экономистов, программистов математика в профессиональной деятельности является инструментом решения практических задач, а для учителей математики – это система знаний и умений, которые нужно передать подрастающему поколению. Именно поэтому будущим учителям желательно глубоко изучить логическое строение математики, ее аппарат и основательно усвоить математические методы познания окружающего мира.
Во время изучения математического анализа в университете будущий учитель овладевает определенным набором знаний, умений и навыков, которые помогут работать в условиях профилирования старшей школы. Современных учеников молодому учителю заинтересовать не просто. Теоретический материал не в полной мере отражает существующие межпредметные связи. Например, изучая тему «Производная и ее приложение» по классическим учебником студенты могут ознакомиться лишь с геометрическим и механическим содержанием производной.
Цель исследования – раскрыть пути реализации прикладной направленности курса «Математический анализ» с помощью системы прикладных задач в процессе подготовки будущих учителей математике в педагогическом университете.
Материалы и методы исследования
Рассматривая содержание учебного материала по математическому анализу для педагогических университетов, нужно обратить внимание на то, что основным заданием этих университетов является, прежде всего, подготовка высококвалифицированных педагогических кадров – учителей средних школ. Как показывает анализ программ по математическому анализу, их содержание учитывает не все направления деятельности будущего учителя математики. Недостаточно внимания уделяется прикладной направленности курса и методике ее реализации [9].
Организация учебного процесса в педагогическом университете по изучению студентами курса «Математический анализ» предусматривает реализацию двух основных составляющих: изучение теоретического материала и применение его к решению задач. Анализ основных подходов к отбору и структуризации содержания образования позволяет утверждать, что последовательность изложения учебного материала должна отображать и воспроизводить логическую структуру современного состояния соответствующей научной отрасли, в полной мере отображать учебный план, а также соответствовать закономерностям развития познавательных возможностей студентов.
Содержание курса «Математический анализ» как учебного предмета, который формирует компетентности будущего учителя, строится на общих целях государственного стандарта высшего образования. В учебной программе рассматриваемого курса предусмотрен определенный порядок изучения разделов и тем. В соответствии с отраслевыми стандартами высшего образования по специальности «Математика» курс «Математический анализ» в высших педагогических учебных заведениях Украины состоит из таких блоков: ПП.06.01. Введение в анализ; ПП.06.02. Дифференциальное исчисление функций одной переменной; ПП.06.03. Интегральное исчисление функций одной переменной; ПП.06.04. Числовые и функциональные ряды; ПП.06.05. Дифференциальное исчисление функций многих переменных; ПП.06.06. Интегральное исчисление функций многих переменных; ПП.06.07. Элементы функционального анализа; ПП.06.08. Мера и интеграл Лебега [2].
В процессе изучения математического анализа в педагогическом университете студент должен овладеть определенной системой знаний и умений по основным вопросам курса (усвоить систему понятий и овладеть аппаратом дифференциального и интегрального исчисления, научиться использовать полученные знания для решения абстрактных и прикладных задач). Кроме этого у студентов следует развивать математические способности, формировать высокий уровень математического мышления и другие профессиональные умения, необходимые учителю в его педагогической деятельности. В настоящее время возникла необходимость усовершенствовать структуру и содержание системы задач по математическому анализу, а именно дополнить ее прикладными задачами.
Прикладные задачи, которые используются на лекциях, практических занятиях и во время самостоятельной работы, способствуют лучшему пониманию и усвоению теоретического материала, а также формированию у студентов умений применять изученное на практике. Известно, что от степени заинтересованности студентов предметом зависит характер их внимания и активность во время занятий.
Структура системы задач отвечает последовательности изучения соответствующих разделов курса математического анализа согласно программе курса «Математический анализ». В соответствии со структурой курса «Математический анализ» мы выделяем восемь учебных тем, на которых целесообразно показать прикладное направление, то есть разное толкование определенного понятия, а именно: производная и ее приложение, дифференциал, неопределенный интеграл, определенный интеграл и его приложение, производные функции частей многих переменных, двойные интегралы, тройные интегралы, криволинейные интегралы.
Проанализировав большинство учебников и учебных пособий, которые используются при изучении курса «Математический анализ», можно утверждать, что в них прикладным задачам уделяется очень мало внимания.
Деятельность учителя математики в современной школе требует более широких знаний, поскольку с 2010-2011 учебного года в соответствии с Концепцией профильного обучения [8] старшая общеобразовательная школа полностью перешла на профильное обучение школьников. Определены основные направления профилирования (естественно-математический, филологический, общественно гуманитарный, художественно-эстетический, спортивный, технологический, универсальный). Задаются уровни изучения математики для каждого профиля (уровень стандарта, академический уровень, уровень профильной подготовки), утверждены соответствующие учебные планы и программы [4-7, 10]. Усвоение содержания образования в общеобразовательных заведениях с профильным обучением должно, во-первых, обеспечивать общеобразовательную подготовку школьников, во-вторых – подготовку к будущей профессиональной деятельности. Математика является обязательной учебной дисциплиной для изучения школьниками в классах всех профилей. Одновременно она является и профильным предметом для классов естественно-математического направления и некоторых других.
В Концепции профильного обучения отмечается, что профильные предметы обеспечивают прикладную направленность обучения за счет интеграции знаний и методов познания и применения их в разных сферах деятельности, в том числе и профессиональной, которая определяется спецификой профиля обучения [8].
В Программе по математике для уровня профильной подготовки указывается, что она предназначена для организации обучения математики в классах математического, физического и физико-математического профилей.
В Программе по математике для академического уровня отмечается, что она предназначена для организации обучения математики в классах биолого-химического, биолого-физического, биотехнологического, химико-технологического, физико-химического, агрохимического профилей естественно-математического направления профильного обучения, а также технологического направления (информатика, производственные технологии, проектирование и конструирование, менеджмент, бытовое обслуживание, агротехнологический и другие).
Как видим, для учеников разных профилей, например менеджмента и биолого-химического, предлагается одинаковое содержание программы по математике. Обеспечить прикладную направленность обучения, как это определено нормативными документами, можно за счет разнообразия системы задач – включением прикладных задач, содержание которых отвечает профилю обучения. Современные школьные учебники содержат определенное количество прикладных задач, которые касаются применения математических методов в разных науках и сферах деятельности человека, но для каждого конкретного профиля их недостаточно. Поэтому будущий учитель за время обучения в университете должен научиться решать прикладные задачи разного содержания и добирать такие задачи в соответствии с определенным профилем обучения школьников. Определенная работа в этом направлении, безусловно, осуществляется на занятиях по методике обучения математики, но умение решать определенные виды прикладных задач методом интегрального и дифференциального исчисления желательно формировать у студентов в процессе обучения математического анализа.
Чтобы показать студентам конкретные примеры использования производной в разных отраслях, необходимо было проанализировать соответствующие учебники и учебные пособия. Проведенный нами анализ учебников по экономике дал возможность раскрыть и выделить экономическое содержание производной.
Экономический смысл производной. Функция потребления и сбережения. Обозначим через y доход, который остается у населения после оплаты налогов. Этот доход состоит из двух частей. Часть дохода население тратит. Эта часть называется функцией потребления, которую обозначают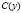 
. Вторая часть 
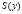составляет сбережение населения и называется функцией сбережения. Следовательно 
.
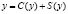Расходы хранения. Совокупные расходы производства товара состоят из расходов его производства и расходов хранения. Пусть товар завозится на склад партиями по x штук в одной партии, а тратится с постоянной скоростью. Тогда наполняемость склада зависит от времени t и задается функцией.
Если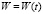 
– количество выработанной продукции в зависимости от времени, тогда
.
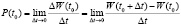Производительность труда. Пусть функция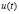 
выражает объем изготовленной продукции y за время t. Тогда производная объема изготовленной продукции по времени 
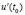является производительностью труда в момент 
.
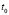Задача 1. Объем продукции V мастерской, которая изготавливает елочные игрушки, на протяжении дня выражается зависимостью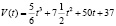 
, где 
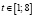. Вычислите продуктивность труда мастерской на протяжении каждого часа работы [1].
Аналогичная работа была проведена с учебниками химии, биологии и другими. Таким образом, в теме «Производная и ее приложение» стало возможным, кроме физического и геометрического, раскрыть химический, биологический, экономический и другой смысл математического понятия производной.
Химический смысл производной. Пусть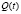 
– концентрация вещества, которая получается во время химической реакции в момент времени t. Тогда 
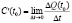– скорость реакции в момент 
.
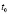Задача 2. Известно, что при мономолекулярной реакции за время t образуется молекул (продукта реакции)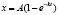 
. За каким законом можно отобразить скорость образования нового вещества при названной реакции?
Биологический смысл производной. Если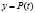 
– закон размножения популяций, тогда 
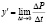– продуктивность популяции в данный момент времени.
Задача 3. Размер популяции бактерий в момент t (время отображено в часах) задается формулою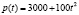 
. Найти скорость роста популяций в момент 
.
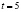В будущем это даст возможность учителю корректно создавать математические модели к разным реальным процессам и рационально решать прикладные задачи, которые касаются разных отраслей науки и человеческой жизнедеятельности.
Поскольку в учебной программе по курсу «Математический анализ» отмечаются межпредметные связи со смежными дисциплинами: общая физика, теоретическая физика, теоретическая механика, астрономия, методика математики [9], то в контексте нашего исследования заслуживают на внимание физический, биологический, химический и экономический смысл понятия «производная».
С помощью рекомендованной литературы детализировать физическое содержание производной для угловой скорости и углового ускорения, теплоемкости и силы тока студенты могут самостоятельно, поскольку эти понятия знакомые им из школьного курса физики. Желательно, чтобы на практическом занятии студенты имели бы возможность проверить результаты самостоятельной работы. Сделать это можно с использованием таблиц или презентаций, на которых поданы такие сведения.
Чтобы ознакомить студентов с экономическим, химическим, биологическим содержанием производной нужно найти дополнительное время на лекции или практических занятиях, или организовать индивидуальную деятельность студентов в виде учебных проектов, работы кружка и так далее. На помощь студентам и преподавателям математического анализа нами подготовлено учебное пособие «Прикладные задачи по математическому анализу» [3], в котором подан минимально необходимый объем сведений о применении методов математического анализа.
Данное учебное пособие разработано в соответствии с Государственным образовательным стандартом высшего образования для бакалавров специальности «Математика». Структура пособия отвечает последовательности изучения соответствующих разделов курса «Математический анализ» для математиков согласно программе по математическому анализу. Каждый параграф содержит отдельные короткие блоки теоретических сведений, наводятся основные определения, главные формулы, которые применяются при решении задач. Этот материал позволит студентам, не отвлекаясь на поиски необходимых формул, больше времени уделить самостоятельному решению задач.
В классическом курсе математического анализа прикладные задачи не выделяются по содержанию (природоведение, физика, химия, биология, экономика), а подаются в соответствии с учебными темами. В то же время есть потребность дополнить курс математического анализа подборками задач, которые касаются определенных направлений науки. Такие задачи помогут студентам лучше понять применение методов математического анализа и более сознательно их использовать в решении прикладных задач. В будущей профессиональной деятельности учителя смогут использовать эти задачи для реализации прикладной направленности школьного курса математики.
Результаты исследования и их обсуждение
На основе анализа программ курса «Математический анализ», видов прикладных задач, которые решаются его методами, и отраслей научных знаний, где эти задачи возникают, построена спецификация курса и подана в нашем учебном пособии [3].
Результаты педагогического эксперимента и собственный опыт работы показали, что прикладные задачи в пределах учебных тем целесообразно группировать по отраслям науки и решать в определенной последовательности (от более знакомой отрасли к менее знакомой). Это позволяет более быстро и четко понять отрасль применения прикладной задачи, углубить знания из смежных дисциплин и расширить мировоззрение студентов и будущих учителей математики.
Выводы. Для того, чтобы показать прикладную направленность курса «Математический анализ», следует в его структуре выделять восемь учебных тем, а раскрыть их можно с помощью решения задач с физическим, химическим, биологическим и экономическим содержанием, где у студентов возникает необходимость переводить содержание задачи на язык математической модели.
Изучение курса «Математический анализ» должно ознакомить студента с математическими методами исследования, а также поднять его математическую культуру к уровню современных требований, которые выдвигают к учителю математики в школах разного профиля. Решение задач способствует лучшему пониманию и усвоению теоретического материала, умению студентами применять на практике общие теории. Будущие учителя должны не только знать теоремы и делать элементарные превращения, но и понимать их смысл в науке и ее приложениях. Система будет неполной без задач прикладного характера.
Библиографическая ссылка
Дмитриенко О.А. СИСТЕМА ПРИКЛАДНЫХ ЗАДАЧ В КУРСЕ МАТЕМАТИЧЕСКОГО АНАЛИЗА // Международный журнал экспериментального образования. – 2013. – № 10-1. – С. 133-136;URL: https://expeducation.ru/ru/article/view?id=4140 (дата обращения: 27.12.2024).