Для улучшения лечебного эффекта препаратов необходимо повышать деятельность специфических и неспецифических звеньев защиты, усиливать гибкость ответных компенсаторно-приспособительных реакций в рамках универсальных постагрессивных адаптационных реакций (ПАР), например, с помощью особых физических способов, химических и биологических средств направленного действия на их этиологическое и патогенетическое звено [11].
С учетом изложенного, разработка показаний, теоретическое и патофизиологическое обоснование комплексного применения биологически активных препаратов при лечении ГВЗ приобретает особую актуальность, причем, решение этой важной проблемы имеет не только большое медицинское, но и социально-экономическое значение при решении практических задач охраны здоровья.
Отсутствие объективных критериев оценки показателей применения биологически активных препаратов сильно затрудняет адекватную коррегирующую терапию ПАР [5, 11].
Использование же современных методов статистической обработки позволит распределить больных по характеру и интенсивности проявления патологического процесса на группы с »благоприятным» и »неблагоприятным» вариантом течения заболевания. В свою очередь, такой «синдромальный» анализ проявления процесса дает возможность определить в структуре изучаемых реакций уровень долевого участия этих симптомов. Исследование корреляционных (кооперативных) связей симптомов позволит определить конкретно требуемое звено приложения для препаратов, применяемых для патогенетической медикаментозной коррекции патологического процесса.
1. Характеристика основного эксперимента и полученного тестового массива данных. Изучение характера течения постагрессивных адаптационных реакций у больных с гнойно-воспалительными заболеваниями, гнойными осложнениями ран основывалось на клиническом анализе результатов лечения 142 больных. Из них 1-ю группу составил 21 больной с гнойными ранами, 2-ю группу – 18 пострадавших с сочетанными травмами, 3-ю группу – 28 больных с гнойными послеоперационными ранами, 4-ю группу – 41 больной с травматическим остеомиелитом и 5-ю – 34 больных с флегмонами. Все больные находились на лечении в клиниках военно-полевой хирургии ВмедА , НИИ скорой помощи им. И.И. Джанелидзе и 8 отделения НОКБ 2006-2012 гг.
В данном методическом руководстве тестовый массив состоит из 26 больных с флегмонами ЧЛО: из них 16 больных с неблагоприятной и 10 – с благоприятной формами течения болезни. Все больные наблюдались в 4-х временных точках: на 1-е, 7-е, 14-е и 21-е сутки.
Рассмотрим клиническую значимость ряда основных показателей, достаточно полно характеризующих, по нашему мнению, уровень резистентности организма, а также их динамику у больных с флегмонами челюстно-лицевой области, гнойными послеоперационными ранами.
Как мы полагаем, эти показатели предопределяют важные морфологические и биохимические механизмы постагрессивных реакций, причем их функции генетически детерминированы. Следовательно, предлагаемое изучение динамики изменения этих показателей в процессе лечения, а также исследование изменения биологических реакций организма на контакт с медикаментами, влияние этих реакций на течение воспаления или раневой болезни даст объективную информацию о динамике патологического процесса и эффективность его коррекции.
В приведенном ниже списке показателей (признаков) заболевания указан код, номер признака и его физиологические уровни значимости[1]
Ig A / (1) Иммуноглобулины А (1.42-1.98 × 0.16г/л).
РТМЛ / (2) Реакция торможения миграции лейкоцитов (40-75 %). настоящей работе мы изучали РТМЛ с конкавалином А – специфическим митогеном в отношении Т-лимфоцитов.
Л / (3)Лейкоциты (4-8,8×109/л).
М / (4)Моноциты (0.290-0.6×109/л).
Лф / (5) Лимфоциты (1.2-3.0×109/л) – основа как клеточного, так и гуморального иммунитета – предшественник антителообразующей клетки и носитель иммунологической памяти (Петров Р.В. с соавт., 1982).
ЛИИ / (6) ЛИИ – лейкоцитарный индекс интоксикации по Я.Я. Кальф-Калифу (0.5-1.0) – показатель тяжести патологического процесса и прогноз заболевания
(С+2П+3Ю+4Ми)(ПлК+1)
ЛИИ = –––––––––––––––––––––––––,
(Мон+Лимф)(Эоз+1)
где С – сегментоядерные нейтрофилы; П – палочкоядерные; Ю – юные; Ми – миелоциты; Плк – плазматические клетки; Мон – моноциты; Лимф – лимфоциты; Эоз – эозинофилы.
Повышение ЛИИ до 3.0 единиц указывает преимущественно на ограниченный характер процесса, а его повышение до 4.0 и более – на значительную эндогенную интоксикацию.
РЭ / (7) Активность раневых энзимов (более 111.5 МЕ/л в 1 фазе раневого процесса, менее 80 МЕ/л – во 2 фазе) – косвенный признак регенерационной активности ран [11].
КФА / (8) Коэффициент функциональной активности моноцитов (1,7 ± 0.09) – отношение активных и неактивных форм моноцитов.
ЩФ / (9) Активность щелочной фосфатазы в сыворотке крови (278830 нмоль/(с×л)). ЩФ (К.Ф.3.1.3.1.).
АМ / (10) Амплитуда моды R-R интервала на кардиоинтервалометрии (сек) – показатель преобладания воздействия симпатической и парасимпатической иннервации на работу сердца у больных и пострадавших с постагрессивными адаптационными реакциями. Данный показатель мы не учитывали, так как он был статистически незначим.
SH/SS / (11) Коэффициент отношения общего содержания окисленных и восстановленных групп цельной крови.
Цель эксперимента с массивом диктует необходимость знакомства с элементарной техникой методологий последовательного анализа выборок и индивидуумов.
Первичная обработка данных. Статистический вывод – это тонкая грань между нашими предположениями о структуре объекта исследования и реальными наблюдениями. Цель статистического анализа данных – повышение качественного уровня понимания предмета исследования. Этот процесс подчиняется определенным законам. Один из них (принцип иерархичности уровней точности) гласит: «Менее точные уровни исследования оказывают большее влияние на результат» [5]. Поэтому первичная обработка данных является самой важной и сложной частью статистического исследования. К ней приходится возвращаться на всех последующих этапах обработки данных. Какие проблемы стоят на этом этапе?
Типы наблюдений. Природа признаков. Прежде всего, следует разобраться, с каким типом наблюдений мы имеем дело. Полезна следующая четверка исходных понятий статистики – индивиды, признаки, значения признаков и параметр. Индивиды – те объекты, с которых в процессе наблюдений снимаются некие их характеристики (показатели), называемые признаками. Значениями признаков являются: числа, для количественных показателей (например, 175 см. – значение признака «рост»), и градации для качественных признаков. Например, для такого качественного показателя, как тип патологического процесса имеются следующие фонологические аспекты (градации): «флегмона», «сочетанные травмы» и т.д.
Классические методы статистики развивались в основном для количественных признаков. Обработка данных качественных признаков представляет собой наиболее сложную задачу статистики. Здесь можно выделить три главных направления:
1. Шкалирование;
2. Использование информационных статистик;
3. Дисперсионный анализ.
Первое и третье направления связанны с идеей подбора для градаций каких-то числовых значений. Применение различных шкал требует исследования клинической значимости признака. В дисперсионном анализе значения качественного признака (фактора) кодируются средними показателями по градациям из значений одновременно наблюдаемого количественного признака (отклика). Эти методы мы рассматривать не будем.
Информационными статистиками называются функции от выборочных наблюдений, зависящие только от частот.
Важным частным случаем качественных признаков является ситуация, когда их градации можно упорядочить. В этом случае значениям можно приписать числа (ранги), имеющие смысл порядкового номера градации с учетом повторностей ее появления в выборке. В настоящее время ранговая статистика бурно развивается как часть непараметрических методов. Поясним процедуру ранжирования (т.е. приписывания рангов) на примере.
Для признака «состояние больного» упорядоченными значениями могут быть: Т – «тяжелое», С – «средней степени тяжести», У – «удовлетворительное». Если, например, наблюдения 10-ти больных показали следующие их состояния:
(С, Т, С, У, С, У, С, У, С, С),
то, упорядочивая их, имеем:
Т, С, С, С, С, С, С, У, У, У,
1 2 3 4 5 6 7 8 9 10
и сопоставляя каждому значению, его номер по порядку, усредняя номера для одинаковых значений, получаем в качестве значений признака их ранги (значению Т соответствует в данной выборке ранг 1, С – ранг 4,5 , У – ранг 9). Таким образом, наша выборка после ранжирования примет вид
4,5 ; 1 ; 4,5 ; 9 ; 4,5 ; 9 ; 4,5 ; 9 ; 4,5 ; 4,5).
С ней можно обращаться как с выборкой из количественного признака: искать числовые характеристики для рангов, строить ранговые критерии и т.д.
Параметр – показатель неопределенности статистического эксперимента в теоретических конструкциях. Параметрические модели в статистике содержательно более богаты, чем непараметрические, ибо в них присутствует предыдущий опыт исследования проблемы.
По своей структуре можно выделить следующие типы наблюдений: матрицы, процессы, более сложные конфигурации (например, латинские квадраты или блок-схемы в дисперсионном анализе и т.д.). В отдельный тип (назовем его прочерки или артефакты) следует отнести наблюдения, в которых имеются пропуски значений признаков по техническим или каким-либо другим причинам.
Матрицы наблюдений – это прямоугольные таблицы значений xij признаков (номера признаков i , изменяют от 1 до k ) на индивидах (с номерами j, меняющимися от 1 до n). В электронной таблице исходных данных компьютерной системы STATISTICA признакам соответствует название «Variables – Переменные», а индивидам – «Cases – Случаи». Предполагается, что индивиды независимы и образуют повторную выборку объема n. В случае одномерного количественного признака (k=1) повторная выборка представляет собой набор из n чисел: (x1, x2, ... , xn) – его значений, полученных в результате n независимых повторений одного и того же эксперимента. В реальности получение повторной выборки часто является непростой проблемой.
Признаки, наоборот, зависимы между собой. Более того, зависимость между признаками и является чаще всего предметом исследования. Исследование взаимосвязей между указанными признаками лежит в основе статистического решения определенных выше задач. Например, в приводимой в табл. 1 матрице наблюдений указаны значения 9 признаков в четырех временных точках (столбцы) для 26 индивидов (строки). Эта таблица является матрицей наблюдений для тестового массива, в ней n=26 и k=9. Приведенные значения получены из историй болезней 26 больных.
Наблюдения типа процессов представляют собой, как правило, динамику изменения во времени рассматриваемого признака. Значения наблюдаемого признака в разные моменты времени зависимы между собой и, следовательно, не могут рассматриваться как повторности. Но если для каждого (повторного) больного из данной группы (выборки) имеется свое изображение динамики изменения признака, то мы говорим о повторных реализациях процесса (или реализации процесса с повторностями). Для наглядной визуализации данного процесса на рис. 1. представлена динамика уровней лимфоцитов на 1, 7, 14 и 21-е сутки.
Тестовый массив данных. Клинико-лабораторные показатели
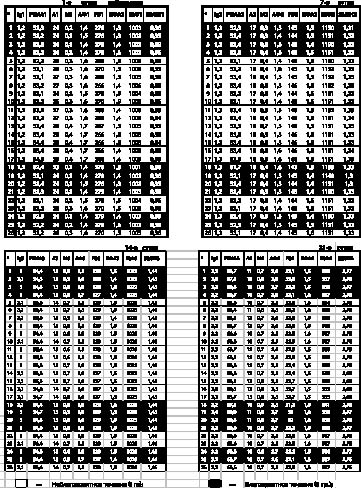
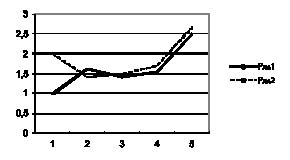
Рис. 1. Динамика уровней лимфоцитов в 1-е (1), 7-е (2), 14-е (3) и 21-е (4) сутки у больных 1-й группы с неблагоприятным течением ПАР (1-й ряд) и 2-й группы с благоприятным течением ПАР (2-й ряд)
Если в матрице наблюдений имеются прочерки технического плана, то есть не связанные с существом дела (потеряна часть данных или они не наблюдались по техническим причинам), то не следует вставлять вместо пропусков искусственные значения признаков. Следует либо удалить соответствующие индивиды или признаки, либо, если это невозможно (например, мал объем оставшейся выборки) предсказывать пропущенные значения признака, по остальным признакам с учетом такой замены в выводах. Борьба с артефактами является непростым вопросом [4]. В системе STATISTICA есть специальные команды для различных стратегий решения этой проблемы. Например, замена прочерков на средние значения.
Гистограммный анализ. Наглядное представление об исходной выборке обычно задается в виде различных диаграмм распределений частот значений признака в выборке. Отметим важную терминологию. Неодинаковые значения признака, упорядоченные по возрастанию, называются вариантами. В выборке вариантам соответствуют частоты (повторности вариант). Представление выборки в виде набора вариант с набором их частот называется вариационным рядом. Набор выборочных частот для всех значений признака называется выборочным распределением признака. Полный набор вероятностей, с которыми признак может принимать свои значения, называется генеральным распределением признака. Все характеристики распределений могут рассматриваться на выборочном и генеральном уровнях.
Генеральный уровень соответствует более объективному анализу данных. Поэтому часто целью статистического анализа является исследование генеральных свойств признака на основе выборочных наблюдений. Функции от выборочных наблюдений, рассматриваемые на генеральном уровне называются статистиками[2].
Среди диаграмм для выборочных распределений наиболее часто используются гистограммы, которые строятся следующим образом. Область значений признака разбивается на интервалы одинаковой длины и над каждым интервалом строится прямоугольник, площадь которого равна числу выборочных наблюдений, попавших в данный интервал. Наиболее часто встречающиеся варианты называются модами. На гистограмме модам соответствуют прямоугольники с максимальными высотами. Гистограммный анализ позволяет ответить на очень важные вопросы об однородности и точности выборочных наблюдений.
На результаты наблюдений существенное влияние может оказывать прибор, используемый в эксперименте (роль прибора может играть и человек). Обычно влияние прибора характеризуют систематической и случайной ошибкой. Но можно уменьшить влияние таких шумов (навести контрастность) и на уровне всего распределения в гистограммном анализе при достаточном числе наблюдений. Для этого следует сравнивать гистограммы при различных значениях длины интервала разбиения (процедура «стягивания окна»). Моды, которые сохраняются при такой процедуре, называются устойчивыми. Длина интервала разбиения, при которой все устойчивые моды сохранены, а случайные моды исчезли, определяет истинную (внутреннюю) точность данных наблюдений[3].
На рис. 2 видно, что разбиение на 26 интервалов (случай А) слишком мелкое – много случайных мод. Случай В слишком груб. Точность данных лучше всего соответствует случаю Б, где наблюдаются две устойчивые моды. Материал неоднороден по этому признаку. В нем смешаны две различные совокупности исходных данных, отражающих характер течения патологического процесса.
Однородная выборка характеризуется симметричной гистограммой с одной устойчивой модой и может интерпретироваться как наблюдение постоянного значения (константы), зашумленного случайными ошибками прибора. В этой ситуации, в случае непрерывного признака, чаще всего ей соответствует генеральное распределение, называемое нормальным. Оно полностью определяется двумя параметрами: генеральным средним (оно называется математическим ожиданием) и (генеральной) дисперсией.
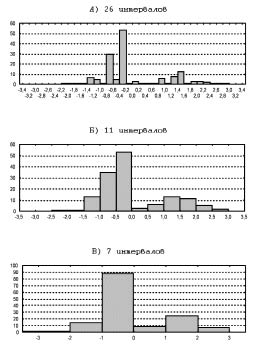
Рис. 2. Процедура «стягивания окна» на примере общего массива больных. В качестве признака выбран 2-й фактор на 1-е сутки наблюдения
Полимодальность гистограммы – показатель существенной неоднородности выборки. Для правильности дальнейших выводов важно понять естественную природу такой неоднородности. В реальных медицинских данных гистограмма, не противоречащая предположению о нормальном распределении, часто оказывается несимметричной, но, как правило, унимодальной (рис. 3).
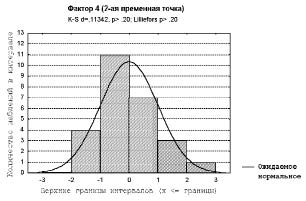
Рис. 3. Пример гистограммы близкой к показателю однородной выборки. В качестве признака выбран 4-й фактор во второй временной точке тестового массива
Выводы
Организационные и экспериментальные аспекты развиваются по своим законам, которые постоянно приходится учитывать. Наибольшие трудности представляет методология, то есть согласование традиционного языка описания эксперимента с принятой терминологией в методах обработки его результатов. Лучшее всего иметь постоянный контакт с профессионалом – математиком, но многое можно сделать и самостоятельно, учитывая современный прогресс в компьютерной технике вычислений и сервиса представления данных. Помощь в этом и является конкретной целью данных методических указаний. Основным техническим инструментом в систематизации наблюдений является система статистических программ для персональных компьютеров STATISTICA.
Библиографическая ссылка
Мадай Д.Ю., Мадай Д.Ю., Вебер В.Р., Гривков А.С., Барт В.А., Мадай О.Д., Гурин А.В., Никитина Е.А., Безуглая Т.О. КОМПЛЕКСНЫЙ ПОДХОД К ОЦЕНКЕ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ // Международный журнал экспериментального образования. 2013. № 11-2. С. 40-46;URL: https://expeducation.ru/ru/article/view?id=4313 (дата обращения: 01.02.2026).

