Рассматривается алгоритм построения современного АЦП, с использованием прикладной программы MathCAD, которая содержит сотни операторов и встроенных функций для решения разных технических задач, документирования всех вычислений в процессе их проведения, прослеживания процессов и операций в реальном времени [1].
Построение и анализ модели АЦП поразрядного уравновешивания (или по-другому метод последовательного приближения) имеет целью определения номера разряда аналогово-цифрового процессора соответствующего измеряемому напряжению.
В данном методе сравниваются опорное напряжение и измеряемое напряжение. При пошаговом сравнении напряжений выводится двоичный код, который получается после следующих действий: если опорное напряжение больше, чем измеряемое, то разряд равен «1», если же меньше, то разряд равен «0». Для N-разрядного АЦП необходимо совершить N таких шагов [2]. Для решения задачи необходимо ввести константу, а именно рассчитать значение напряжения равное единице разряда. К примеру: опорное напряжение Vref:=4; измеряемое напряжение Vin:=2; разрядность N:=4, то:
![]() (1)
(1)
Для получения результата в программе в MathCAD, операцию сравнений напряжений включаем в цикл while, и будем выполнять программу пока последующее деление опорного напряжения, не станет равной или меньше «1».
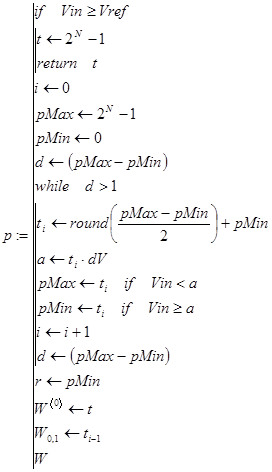 (2)
(2)
В последующей матрице: в первом столбце значение разряда найденного напряжения в каждом выполненном цикле; во втором значение разряда соответствующего измеренному напряжению:
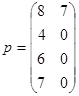 (3)
(3)
Выведем значение разряда измеряемого напряжения, соответствующий ему двоичный код, напряжение соответствующее найденному номеру разряда и погрешность метода:
![]()
![]()
![]()
![]() (4)
(4)
В результате исследования можно сделать вывод: чем больше разрядность АЦП, тем меньше погрешность результата преобразования.
Библиографическая ссылка
Никонова Г.В., Бронникова А.В. МОДЕЛИРОВАНИЕ АНАЛОГО-ЦИФРОВОГО ПРЕОБРАЗОВАТЕЛЯ B ЗАДАЧАХ ОБРАБОТКИ СИГНАЛОВ // Международный журнал экспериментального образования. 2014. № 1-2. С. 147-148;URL: https://expeducation.ru/ru/article/view?id=4576 (дата обращения: 02.03.2026).

