Введение
В последние годы цифровая обработка сигналов (ЦОС) занимает доминирующее положение в системах и средствах передачи и обработки информации в связи с неоспоримыми достоинствами – точность, гибкость и высокая скорость обработки. Кроме того, с развитием средств вычислительной техники системы ЦОС становятся все дешевле и компактнее. Эффективность ЦОС полностью определяется объемом вычислений, которые получаются при реализации математической модели процесса цифровой обработки сигнала с помощью специализированного процессора (СП). Снижение объема вычислений приводит к уменьшению аппаратурных затрат при реализации систем ЦОС или к повышению производительности вычислительного устройства. Таким образом, выбор алгебраической системы оптимальной с точки зрения минимума объема вычислений при реализации методов ЦОС является актуальной и важной.
Постановка задачи исследований. Как правило, в подавляющем большинстве приложений задачи ЦОС сводится к нахождению значений ортогонального преобразования конечной реализации сигнала для большого числа точек, что предопределяет повышенные требования к скорости обработки и разрядности вычислительного устройства. Решить данную проблему можно за счет перехода от одномерных вычислений к многомерным. В основу данного преобразования положена китайская теорема об остатках (КТО) [1-5].
Особое место среди таких систем занимает модулярная полиномиальная система класса вычетов, с помощью которых возможна организация ортогональных преобразований сигналов в расширенных полях Галуа 
. Если исходное число А представить в полиномиальной форме, а в качестве оснований выбрать минимальные многочлены поля Галуа, то справедливо
A (z) = (α1 (z), α2 (z).., αn (z)), (1)
где αi (z) ≡ A (z mod pi(z); pi (z) – минимальный многочлен.
Применение модулярных полиномиальных кодов позволяет свести операции в кольце полиномов к соответствующим операциям над остатками [1-6]. В этом случае
, (1)
где
и 
- модулярный код в кольце полиномов; 
; 
; 
- операции сложения, вычитания и умножения в GF(p); l = 1, …,n.
Таким образом, основным достоинством непозиционных кодов является, то, что данные представляются в виде малоразрядных остатков, которые обрабатываются по параллельным вычислительным трактам. Это позволяет повысить скорость вычислений, что и предопределяет интерес к полиномиальным непозиционным кодам в различных областях применения [1-6].
В работах [1-5] предлагается для эффективной реализации ортогональных преобразований с высокой точностью и скоростью вычислений реализация дискретного преобразования Фурье (ДПФ) в кольце полиномов. В этом случае, если имеется кольцо полиномов P(z), с коэффициентами в виде элементов поля GF(p), то данное кольцо разлагается в сумму
, (2)
где Pl(z) – локальное кольцо полиномов, образованное неприводимым полиномом pl(z) над полем GF(p); l=1, …, n.
При этом в кольце полиномов можно организовать ортогональное преобразование, представляющее собой полиномиальное ДПФ, вида
, (3)
где 
, l=1,2,…,m; k=0,1,…d-1.
При этом должны выполняться следующие условия:
1. 
- первообразный элемент порядка d для локального кольца Pl(z).
2. d имеет мультипликативный обратный элемент d*.
Если отмеченные условия выполняются, то получается циклическая группа, которая имеет порядок d. В этом случае ортогональное преобразование является полиномиальным ДПФ для кольца вычетов P(z) если существуют преобразования над конечным кольцом Pl(z)
Поэтому ДПФ над Pl(z) можно обобщить над кольцом P(z), если конечное кольцо Pl(z) содержит корень d-ой степени из единицы и d имеет мультипликативный обратный элемент d*, такой что справедливо
. (4)
Основным достоинством системы класса вычетов является сравнительная простота выполнения модульных операций (сложения, вычитания, умножения). Формальные правила выполнения таких операций в МПК позволяют существенно повысить скорость вычислительных устройств ЦОС [5].
Кроме модульных операций, позволяющих повысить скорость обработки информации, модулярные коды позволяют обнаруживать и исправлять ошибки, возникающие в процессе функционирования СП. Если в качестве рабочих оснований выбрать k минимальных многочленов МПК (k<n), то данные основания определяют рабочий диапазон
. (5)
Если 
, то такой полином считается разрешенным и не содержит ошибок. В противном случае, полином, представленный в модулярном полиномиальном коде, содержит ошибки [6-10].
Для определения местоположения и глубины ошибки в полиномиальной системе классов вычетов используются позиционные характеристики. В работе [9] представлен алгоритм вычисления такой характеристики как интервальный номер. Синдром ошибки для полиномиального кода вычисляется в работе [8]. В работе [7] показана математическая модель поиска ошибочного основания с использованием алгоритма нулевизации. Структура устройства спектрального обнаружения и коррекции в кодах полиномиальной системы классов вычетов приведена в работе [10].
Одной из характеристик, использующемой при выполнении процедур поиска и коррекции ошибок в модулярных кодах, является след полинома. Для получения данной характеристики используются псевдоортогональные полиномы. Они представляют собой ортогональные полиномы, у которых нарушена ортогональность по нескольким основаниям. Известно, что если в псевдоортогональных полиномах нарушена ортогональность по контрольным основаниям, то данные полиномы являются ортогональными полиномами безизбыточной системы оснований полиномиальной системы классов вычетов.
Для получения псевдоортогональных полиномов проведем расширение системы оснований p1(z), …, pk(z) на r контрольных оснований pk+1(z), …, pk+r(z) и представим ортогональные полиномы в виде:
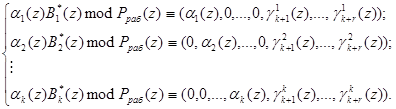(6)
Выражение (6) определяет значения псевдоортогональных полиномов, у которых нарушена ортогональность по контрольным основаниям.
Согласно китайской теореме об остатках
, (7)
полином можно представить в виде:
. (8)
Тогда каждое слагаемое выражения (4) представляет собой
, (9)
где Bi*(z) – ортогональный базис безизбыточной системы оснований МПК.
Подставив выражение (6) в равенство (8), и учитывая, что в процессе выполнения операции не бывает выход за пределы Pраб(z), получаем
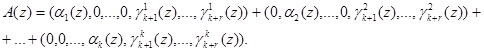
Следовательно, справедливо
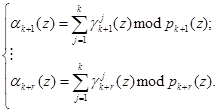(9)
Таким образом, на основании (9) и воспользовавшись значениями псевдоортогональных полиномов, определяемых равенством (6), можно вычислить значения остатков по контрольным основаниям 
согласно
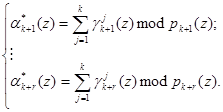. (10)
Затем на основании полученных значений и значений, поступающих на вход устройства коррекции ошибок, можно определить синдром ошибки согласно выражения
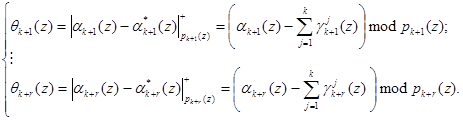(11)
Если разность равна нулю, т.е. 
, то исходный полином является разрешенным и не содержит ошибки. В противном случае модулярная комбинация является запрещенной. Тогда в зависимости от величины синдрома ошибки осуществляется коррекция ошибки, т.е.
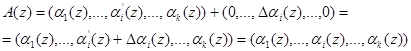(12)
где
- вектор ошибки модулярного кода; 
- глубина ошибки по i-му модулю МПК.
В работе [6] представлена структура устройства для преобразования числа из полиномиальной системы классов вычетов в позиционный код с коррекцией ошибки, в процессе функционирования которого используется данный алгоритм. Следует отметить, что этот алгоритм поиска и коррекции ошибок позволяет осуществить поиск и коррекцию всех однократных ошибок с использованием двух контрольных оснований и 90 процентов двоичных ошибок.
Вывод. В работе показана возможность осуществления цифровой обработки сигналов с использованием математической модели ЦОС, обладающей свойством кольца и поля. Применение полиномиальных кодов позволяет повысить скорость обработки данных за счет применения малоразрядных остатков и их параллельной архитектуре вычислений. Кроме того, МПК могут использоваться для повышения отказоустойчивости вычислительных систем. В работе рассмотрен алгоритм вычислений позиционной характеристики на основе ортогональных базисов, у которых нарушена ортогональность по контрольным основаниям.
Патент России № 2301441. Бюл. № 17 от 20.06.2007.
Библиографическая ссылка
Барсагаев А.А., Калмыков М.И. АЛГОРИТМЫ ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В МОДУЛЯРНЫХ ПОЛИНОМИАЛЬНЫХ КОДАХ // Международный журнал экспериментального образования. – 2014. – № 3-1. – С. 103-106;URL: https://expeducation.ru/ru/article/view?id=4672 (дата обращения: 21.11.2024).