Учитывая, что традиционное, стандартное поведение лекций по математике не соответствует уровню современных требований, предъявляемых к выпускникам-бакалаврам, наш преподаватель математики (соавтор статьи – Часов К.В.) проводит эти занятия с использованием проекционного и интерактивного оборудования. На занятиях практически в любой момент времени возможно проверить тот или иной математический факт в математической среде MathCAD. При этом проверка может быть доверена любому студенту в аудитории, для чего не нужно даже выходить к доске (интерактивной доске) – студенту передаётся беспроводной графический планшет, с помощью которого он и выполняет необходимые манипуляции.
Во время одной из лекций, выясняя свойства преобразования плоскости, была наугад записана матрица этого преобразования. Для невырожденности преобразования матрица должна была иметь определитель, отличный от нуля. Проговаривая эту фразу, лектор вычислил определитель в среде MathCAD и он оказался равным 0. Вторая попытка также привела к результату 0. Анализируя ситуацию, мы выяснили, что в обоих случаях были введены последовательные натуральные числа (отрезок арифметической прогрессии с различными разностями).
Последовало предложение исследовать эту ситуацию для произвольных числовых последовательностей. В ходе исследования было установлено, что для последовательности чисел (любой арифметической или геометрической последовательностей) с заданным законом получения последующих элементов, записанных последовательно в квадратную матрицу 3-го и большего порядков, также получим определитель равный 0.
Нами был сделан следующий важный вывод.
При расчёте определителей любого порядка, начиная с 3-го, наблюдается закономерность: при заполнении элементов квадратной матрицы последовательными членами арифметической (геометрической) прогрессии с любой разностью (знаменателем) получаем определитель равный нулю.
Учитывая, что ручной ввод различных наборов значений элементов матрицы значителен по времени для инициализации матриц была использована программа (функция пользователя) в среде MathCAD (рисунок 1).
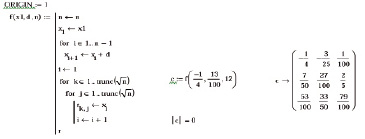
Рисунок 1 – Программа (функция пользователя) в среде MathCAD
Поясним программу, приведённую на рисунке 1: происходит инициализация матрицы, в которой формируется линейный массив заданной длины (3-й параметр функции пользователя), переформируется в двумерный квадратный массив с количеством строк и столбцов, вычисляемым с помощью отбрасывания дробной части корня квадратного из введенного пользователем числа, определяющего количество элементов в матрице, с целью предотвратить возможную ошибку (т.е. число – не квадрат натурального числа) при его вводе. Первый параметр – первый элемент арифметической прогрессии, второй – разность прогрессии.
Очевидно, что программа для геометрической прогрессии строится аналогично, результат получится таким же, как и выше!
Нами было исследовано достаточно большое количество самых различных последовательностей. Получены просто удивительные результаты. По результатам нашего исследования предстоит ещё сделать достаточно серьёзные научные и практические выводы – как их использовать. Это мы и считаем нашей дальнейшей задачей в исследовании прогрессирующих последовательностей (матриц).
Библиографическая ссылка
Смольняков И.М., Часов К.В. НЕКОТОРЫЕ СВОЙСТВА ПРОГРЕССИРУЮЩИХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ // Международный журнал экспериментального образования. 2014. № 7-1. С. 106-107;URL: https://expeducation.ru/ru/article/view?id=5515 (дата обращения: 05.03.2026).

