Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

(), (2)

где являются опытными параметрами. Параметры , входящие в (2), могут быть определены, если известны три значения модуля деформации E1, E2, E3 для трех различных значений z1, z2, z3

Попов Г.Я. в своей работе [5] за функцию (1) предлагает выражение вида

(). (3)

Здесь – опытные данные.

Как известно, что грунт – это минерально-дисперсное тело и обладает определенной пористостью. Здесь при оценке сжимаемости грунтов важно выяснить зависимость между изменениями внешней нагрузки и изменением коэффициента пористости грунтов. Если неоднородная грунтовая среда обладает упругим свойством, то зависимость между коэффициентом пористости и суммой главных напряжений, имеет вид:

,(4)

где

; (5)

- коэффициент пористости для исследуемого момента времени t и глубины z; a(M,t)- зависит от координаты z, т.е. от глубины расположения исследуемой точки уплотняемого грунтового массива. Эта величина может также зависит, и от величины t; - сумма главных напряжений и порового давления для стабилизированного состояния грунтового массива; - начальный коэффициент пористости; - сумма главных напряжений; - коэффициент бокового давления; М – исследуемая точка уплотняемого грунтового неоднородного массива, зависящая от x, y, z. При этом скорость изменения функции (4) для двухфазной среды, согласно [3] имеет вид:

, (6)

где - соответственно определяют оператор Лапласа, значения порового давления в жидкости, объемного веса воды и среднего коэффициента пористости.

Выражение (6) при (4) и (5) приводится к виду:

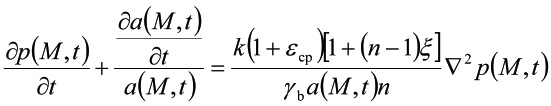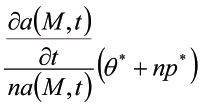+ .(7)

Если коэффициент сжимаемости не зависит от времени, то из (7), находим:

. (8)

Уравнение (8) при (2) и (3) соответственно имеет вид:

; (9)

, (10)

где

.

Выражения (9) и (10) являются уравнениями консолидации упругих неоднородных грунтов соответственно при (2) и (3). В дальнейшем они решаются при определенных краевых условиях.

В настоящее время особую актуальность приобрели проблемы строительства новых и реконструкции существующих объектов в районах распространения слабых водонасыщенных грунтов, что обусловлено особенностью современного развития нефте- и газодобывающих районов Казахстана. При этом возникают не только технологические трудности, связанные с производством работ в особых условиях распространения слабых грунтов, но и повышенные требования к проектным решениям в этой области, как на стадии конструирования, так и во время расчета. Строительства новых высотных сооружений и их эксплуатация сопряжены со значительными затратами ресурсов. В целом проблема является весьма многогранной и, в частности, связана с использованием в основании таких конструкций глинистых водонасыщенных грунтов, для которых свойственны рыхлость, малая плотность и способность разжижаться при нарушении структуры из-за содержания воды, развития пластических деформаций сдвига, многократного промерзания-протаивания в процессе эксплуатации. В связи с этим исследование несущей способности водонасыщенного глинистого грунта в основании сооружений в процессе фильтрационной консолидации является актуальной геотехнической проблемой, имеющей существенное практическое значение и определяющей, в значительной степени, эффективность капитальных вложений, надёжность и нормальную эксплуатацию сооружений.

При проектировании фундаментов промышленных и гражданских сооружений, расположенных на слабых водонасышенных глинистых грунтах всегда надо иметь в виду, чтобы осадка по абсолютной величине была меньшей, чем это допускается и разность этих осадок должна быть крайне минимальной. Однако это не всегда удается выполнять. В большинстве случаев при строительстве сооружений на таких водонасыщенных глинистых грунтах прежде чем строить высотные здания создают искусственные основания, применяя песчаные подушки мощностью от 1-2 м до 7 м. Они позволяют уменьшить глубину заложения фундаментов и увеличивают их устойчивость, а также применение их уменьшает осадки фундаментов. Кроме того, песчаные подушки используются в качестве дренирующего слоя, так как поровая вода из нижележащих водонасыщенных глинистых грунтов отжимается в процессе уплотнения грунтов от веса самой подушки, ускоряя процесс консолидации грунтов основания. К большому сожалению, существующие методы расчета консолидации слабых водонасыщенных глинистых грунтов имели невысокую точность. Видимо, это связано с некоторыми неучтенными явлениями, происходящими в грунтах. В связи с этим, для сильно сжимаемых водонасыщенных глинистых грунтов в начальный момент времени часть нагрузки, мгновенно приложенной нагрузки q к грунту, равная по величине структурной прочности сжатия рстр, сразу же воспринимается скелетом грунта, то

. (11)

Решим уравнение (9) применительно к одномерной задачи уплотнения для двухкомпонентных грунтов. В инженерной практике большой интерес представляют задачи уплотнения земляной среды конечной толщины, обладающей упругим свойством. В связи с этим рассмотрим процесс уплотнения двухфазного грунтового основания с водоупором на глубине находящегося под действием равномерно распределенной нагрузки с интенсивностью q. Тогда граничные условия при ламинарном законе Дарси применительно к этой задаче имеют вид:

; . (12)

Второе граничное условие относится к глубине h, ниже которой фильтрации не происходит.

При этом решение данной задачи относительного порового давления может быть записано так

(13)

где

.

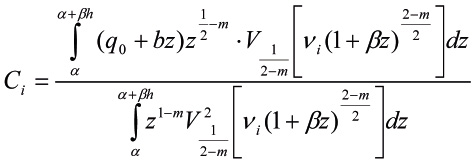Здесь функция зависит от величины . Если она целая, то

, (14)

если же дробная, то

. (15)

Так как экспоненциальная функция быстро убывает при больших значениях показателя, то в (13) ограничимся только первым членом ряда. При этом решение данной задачи относительного порового давления может быть записано так

. (16)

Напряжение в скелете грунта вычисляется по формуле

. (17)

Полученные выражения (16) и (17) соответственно позволяют определить изменения давления в поровой жидкости и напряжений в скелете грунта для любой точки рассматриваемой конечной области уплотнения неоднородного двухфазного грунта, обладающего упругим свойством. После того как определено напряжение в скелете уплотняемого неоднородного грунтового массива, можно вычислить и вертикальные перемещения точек верхней поверхности уплотняемого слоя грунта (осадок). Действительно, если к поверхности слоя грунта приложена некая вертикальная нагрузка, то соответствующая ей осадки s(t), может быть определены по формуле [6], т.е.

, (18)

где h – мощность уплотняемого неоднородного грунтового массива; – начальный коэффициент пористости; z – координата, изменяющаяся по глубине.

Рассмотрим другой случай, когда модуль деформации уплотняемого грунта изменяется по закону (3). Тогда для одномерной задачи давление в поровой жидкости вычисляется по следующей формуле

. (19)

Здесь

. (20)

J0, Y0 – функции Бесселя 1-го и 2-го родов нулевого порядка, которые

имеют вид

;

.

Причем, применяя признак Даламбера, легко установить, что J0 и Y0 сходятся равномерно при всех х.

В выражениях (19), (20) бесчисленное множество значений определяется из следующего уравнения

.

Величина Ri(vi) находится из начального условия (11), т.е. из равенства:

. (21)

Чтобы определить Ri(vi) обе части равенства (21) умножив на , проинтегрируем по z от 0 до h. При этом получим

, (22)

где

, (23)

. (24)

Так как в основном при расчетах интересует всех значение порового давления p(z,t) в течение длительного промежутка времени после начала фильтрационной консолидации (более одного года), то учитывая быстро убывающий характер экспоненциальной функции при больших значениях показателя, достаточно ограничиться только первым членом ряда (19). При этом за расчетную формулу для вычисления порового давления p(z,t), учитывая (19)-(24), можно принять

, (25)

где значения Q01, Q11 находятся из (23) и (24).

Напряжение в скелете неоднородного грунта находятся из следующей расчетной формулы

. (26)

Согласно (18) вертикальные перемещения точек верхней поверхности уплотняемого неоднородного грунтового массива будут вычислены по расчетной формуле

. (27)

В связи с тем, что решение данной задачи приводит к нахождению числовых значений бесселевых функций нулевого порядка, то определение порового давления, напряжения в скелете грунта и осадок уплотняемого грунтового массива можно считать доведенным до конца, так как для функций Бесселя многими исследователями составлены обширные таблицы.

Следует заметить, что эти задачи в различных постановках также решены в [1-3].