Ползучесть грунта по В.А.Флорину[10], есть ни что иное как деформации, обусловленные относительным вязким смещением твердых частиц и агрегатов грунта, а также разрушением цементационных связей. Иначе говоря, под ползучестью грунта подразумевается суммарное значение структурных и структурно - адсорбционных деформаций. Итак, процесс деформирования грунта определяется двумя факторами, фильтрационным уплотнением и ползучестью скелета грунта. В зависимости от значимости для данного грунта каждого из этих факторов могут быть следующие три случая:
- Связи между частицами грунта настолько прочны, что явления выжимания воды из пор не имеет существенного значения. В этом случае можно пренебречь ролью фильтрации и использовать для решения задачи уплотнения теории ползучести.
- Связи между частицами грунта слабы и процесс деформирования в основном обусловлен фильтрационными явлениями. И в этом случае можно ограничиться теорией фильтрационного уплотнения, пренебрегая ролью ползучести скелета грунта.
- Наконец, связи между частицами грунта таковы, что оба фактора деформирования выступают совместно. В таком случае следует пользоваться совместным решением теории фильтрационного уплотнения и теории ползучести.
В большинстве случаев при прогнозировании осадок оснований сооружений возникает необходимость одновременного учета свойства ползучести и старения скелета грунта. При этом старение грунта является результатом уплотнения его под действием внешней нагрузки, а также проявления сцепления упрочнения, обусловленного протеканием во времени физико-химических процессов на контактах твердых и жидких фаз. Его интенсивность зависит от целого ряда факторов и, в первую очередь, от водосодержания и температуры.
Старение грунта можно описать различными алгебраическими выражениями. При этом, учитывая, что деформации ползучести зависят от возраста уплотняемого грунта в момент приложения нагрузки τ и продолжительности действия нагрузки t – τ согласно [1] за меру ползучести можно принять:
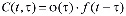 . (1)
. (1)
Здесь – функция, отражающая свойство старения грунта. Причем она при увеличении 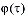 должна монотонно убывать и стремиться к некоторой постоянной величине, характеризующей полностью уплотненный грунт, т.е.:
должна монотонно убывать и стремиться к некоторой постоянной величине, характеризующей полностью уплотненный грунт, т.е.:
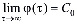
Если под постоянной С0 понимать меру ползучести грунта при t → ∞ , то функция для должна изменяться в интервале
В соответствии с этим в дальнейшем примем
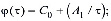
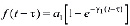 , (2)
, (2)
где С0, А1, a1, y1 – коэффициенты, подбирающиеся по экспериментальным кривым.
Среди всех исследований – работы В.А.Флорина и многочисленные опыты С.Р.Месчана [8] показали приемлемость для описания деформаций скелета стареющего грунта теории упругоползучего тела Г.Н.Маслова-Н.Х.Арутюняна. При этом свойство старения грунта вполне может быть математически описано выражениями (1) и (2).
Кроме того, многочисленные экспериментальные работы по грунтам показали, что при процессе уплотнения эти грунты просто становятся неоднородными материалами. Это связано с изменением модуля деформации и коэффициента сжимаемости грунта в зависимости от координаты уплотняемого массива. В частности, Г.К.Клейн [6] при расчете сооружений, лежащих на сплошном основании, для модуля деформации грунта принимает выражение следующего вида
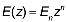 , (3)
, (3)
где En является модулем деформации грунта на глубине z=1; показатель n в большинстве случаев лежит в пределах 0 < n < 2.
Эта модель использована Б.Н. Баршевским [2] для решения некоторых задач консолидации непрерывно-неоднородных грунтов по глубине и получила дальнейшее развитие в работах [12] при решении контактных задач механики деформируемого твердого тела.
В работе Г.Я.Попова [9] при решении подобных задач модуль деформации грунта принят в виде
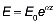 , (4)
, (4)
где E0>0, α – экспериментальные данные; z – координата исследуемой точки по глубине.
В отличие от перечисленных работ ниже будут определены решения задач механики уплотняемой наследстенно-стареющей грунтовой среды, когда модуль деформации грунта считается переменным по глубине. В частности, он может быть представлен в виде степенной или экспериментальной функции.
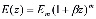 ,
, 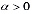 ;
; 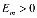 ,
, 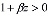 , (5)
, (5)
где 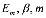 – экспериментальные данные.
– экспериментальные данные.
Для конкретного случая вычисления, они могут быть соответственно приняты следующим образом: 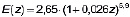 МПа;
МПа; 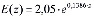 МПа.
МПа.
Таким образом, ниже исследуем процесс консолидации земляных масс, обладающих наследственно - стареющим неоднородным свойством. Для этого введем некоторую ограниченную область трехмерного Евклидового пространства Е3, где происходит процесс уплотнения (консолидации), т.е. G – область изменения пространственных переменных xi, i=1,2,3, а Е3 – совокупность точек, координаты которой определяются тремя этими действительными числами. Пусть Г – граница области, которая должна быть кусочно-гладкой поверхностью, состоящей из конечного числа гладких кусков, а Ω – некоторая область в четырехмерном пространстве Ω = Gx(τ1,T); 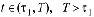 . Ее граница состоит из боковой поверхности Гб = Гx[τ1,T] и двух оснований: нижнего М
. Ее граница состоит из боковой поверхности Гб = Гx[τ1,T] и двух оснований: нижнего М G, t = τ1 и верхнего М
G, t = τ1 и верхнего М G, t = Т. Иными словами, область Ω является областью задания уравнений уплотнения, G – область, соответствующая геометрической форме и размеру уплотняемого тела, в котором изучается процесс уплотнения, а Г – область задания граничных условий xi, i=1,2,3.
G, t = Т. Иными словами, область Ω является областью задания уравнений уплотнения, G – область, соответствующая геометрической форме и размеру уплотняемого тела, в котором изучается процесс уплотнения, а Г – область задания граничных условий xi, i=1,2,3.
Если этот грунт обладает наследственно-стареющим неоднородным свойством, то его состояние, согласно теории упругоползучего тела [1], может быть описано выражением вида:
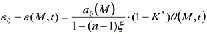 . (6)
. (6)
Здесь ε0 – начальный коэффициент пористости; ξ – коэффициент бокового давления; ε(t) – коэффициент пористости для исследуемого момента времени t; a0(M) - коэффициент сжимаемости, зависящий от глубины уплотняемого грунтового массива x3=z; 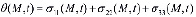 – сумма главных напряжений; n – размерность исследуемой задачи;
– сумма главных напряжений; n – размерность исследуемой задачи;
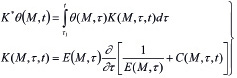 (7)
(7)
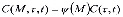 , (8)
, (8)
где 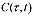 - мера ползучести для однородного грунта, т.е.
- мера ползучести для однородного грунта, т.е.
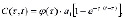 (9)
(9)
где φ – функция старения; a1, y1 – параметры ползучести; E(M) - модуль деформации неоднородного грунта; ψ(M) - функция неоднородности. Она может зависеть от глубины уплотняемого массива. Тогда уравнение уплотнения неоднородного грунта
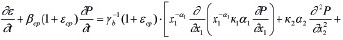
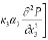 .(10)
.(10)
с учетом его вязкого свойства (6)-(9) приводится к виду:
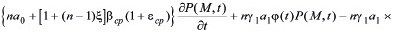
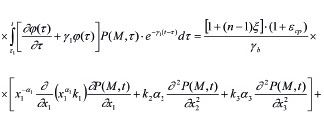
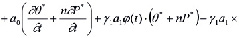
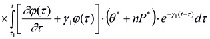 , (11)
, (11)
где β1 - коэффициент объемного сжатия; εср - средний коэффициент пористости; P – давление в поровой жидкости; yb - объемный вес воды; ε0 - начальный коэффициент пористости; θ(M,t) - сумма главных напряжений; n – размерность рассматриваемой задачи; ξ - коэффициент бокового давления уплотняемого грунтового массива; θ*, P* - сумма главных напряжений и давление в поровой жидкости для стабилизированного состояния уплотняемого грунтового массива; αi(i=1,2,3) - в зависимости от мерности задачи принимают значения 0 или 1, т.е. 0˅1. Следовательно из (11 ) при α1 = 0, α2 = α3 =1 находим уравнение, описывающее трехмерное уплотнение грунта; при α1 = α3 = 0 и α2 = 1 – двумерное; при α1 = α2 = α3 =0 – одномерное; при α1 = α2 = 1 и α3 = 0 – осесимметричное, где x1=r, x2=x3. Здесь если пренебречь изменениями пористости среды и порового давления во времени, то из (11) получим уравнения, описывающие распределения порового давления в начальный момент времени. Эти уравнения имеют вид
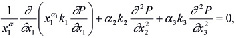 (12)
(12)
где αi(i=1,2,3) в зависимости от мерности задачи принимают значения 0 или 1, т.е. 0˅1.
Выражение (11) является интегро-дифференциальным уравнением и его решение при соответствующих краевых условиях дает возможность определить распределение давлений в поровой жидкости. Это уравнение можно привести к дифференциальному уравнению второго порядка. Для этого (11) продифференцируем по t, затем полученное сложим с (11) предварительно умножив его на y1. В результате имеем:
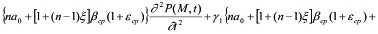
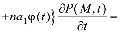
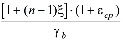
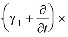
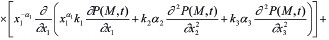
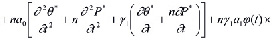
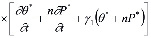 . (13)
. (13)
Выражение (13) является основным уравнением механики многофазных наследственно – стареющих неоднородных уплотняемых грунтов. Откуда при βср =0 находим уравнение уплотнения водонасыщенного грунта, т.е.
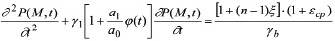
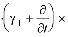
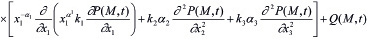 , (14)
, (14)
где
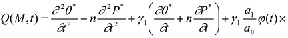
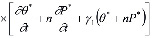 (15)
(15)
Таким образом, получены уравнения механики наследственно - стареющих грунтов при их линейном деформировании. В дальнейшем они будут решены для различных задач уплотнения, имеющие теоретическое и практическое значение в механике уплотняемых пористых сред.
Начальные условия задачи теории консолидации. Так как основное уравнение механики уплотняемых наследственно - стареющих грунтов представлено в виде дифференциального уравнения второго порядка (14) относительно порового давления, то для определения единственного его решения необходимо знать два начальных условия. Одно из них является задание во всех точках области в момент t = τ1 самой функции, т.е.
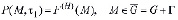 , (16)
, (16)
где функция F(H)(M) непрерывна в точках области 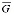 . Эта область есть объединение множества G и его границы Г. В случае одномерной задачи уплотнения грунтов, начальное условие упрощается и соответственно для двухфазной и трехфазной среды имеет вид:
. Эта область есть объединение множества G и его границы Г. В случае одномерной задачи уплотнения грунтов, начальное условие упрощается и соответственно для двухфазной и трехфазной среды имеет вид:
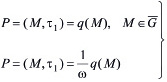 , (17)
, (17)
где коэффициент ω учитывает объемное сжатие грунта за счет газообразных составляющих.
В остальных случаях необходимо решать уравнения фильтрации (14) при соответствующих граничных условиях. Другое начальное условие может быть найдено из (11) учитывая, что при t = τ1 искомое решение должно удовлетворять ему. При этом имеем
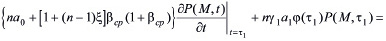
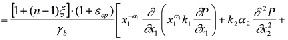
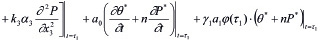 (18)
(18)
Граничные условия задачи теории консолидации. В математической теории уплотнения земляных масс можно встретить три основных разновидностей граничных условий. Первые два условия в общем виде можно представить следующим образом:
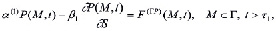 (19)
(19)
где 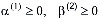 .
.
Если 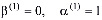 , то имеем первую краевую задачу. В этом случае для любого момента времени задается распределение порового давления или напора на граничной поверхности, а следовательно, и напряжения в скелете грунта. В частности, если жидкость свободно удаляется с некоторой части контура Г уплотняемой среды, то напор или давление на ней равно нулю, т.е.
, то имеем первую краевую задачу. В этом случае для любого момента времени задается распределение порового давления или напора на граничной поверхности, а следовательно, и напряжения в скелете грунта. В частности, если жидкость свободно удаляется с некоторой части контура Г уплотняемой среды, то напор или давление на ней равно нулю, т.е.
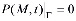 . (20)
. (20)
Если же в (19) примем 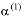 = 0,
= 0, 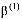 = k (k – коэффициент фильтрации), то имеем второе граничное условие. В этом случае для каждой точки поверхности уплотняемого тела должен быть задан поток жидкости как функции пространственных координат и времени
= k (k – коэффициент фильтрации), то имеем второе граничное условие. В этом случае для каждой точки поверхности уплотняемого тела должен быть задан поток жидкости как функции пространственных координат и времени
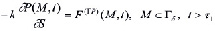 , (21)
, (21)
где S – нормаль к поверхности Г в точке М.
Кроме указанных условий при изучении отдельных задач механики твердого деформируемого тела, можно столкнуться с граничными условиями сопряжения. Эти условия обычно используются в случае контакта нескольких различных тел. В теории уплотнения они применяются при определении НДС многослойных грунтовых оснований.
Постановка задач теории консолидации. Основное уравнение механики уплотняемых в области неоднородных грунтов, полученные в виде (14) при (15) связывают временно - пространственное распределение порового давления внутри исследуемого массива. Чтобы найти его, необходимо знать распределение давлений в поровой жидкости внутри уплотняемого тела в начальный момент времени, геометрическую форму и размеры тела, закон фильтрующей поверхности его между окружающей средой (граничное условие).
Следовательно, при введенных выше обозначениях, краевые задачи уравнения механики уплотняемых наследственно – стареющих неоднородных грунтов формулируются следующим образом: требуется определить в четырехмерном пространстве Ω = Gx(τ1,T); 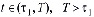 дважды непрерывно дифференцируемое по пространственным координатам, непрерывно дифференцируемое по времени второго порядка и непрерывное вплоть до границы решение P(M,t) уравнений (14), удовлетворяющее краевым условиям исследуемых задач.
дважды непрерывно дифференцируемое по пространственным координатам, непрерывно дифференцируемое по времени второго порядка и непрерывное вплоть до границы решение P(M,t) уравнений (14), удовлетворяющее краевым условиям исследуемых задач.
Ниже в качестве иллюстрации вышесказанного, дадим решение двумерной задачи теории консолидации однородных наследственно – стареющих многофазных грунтов. Для этого рассмотрим процесс уплотнения грунтового массива с водоупором на глубине h. Он ограничен с боков водонепроницаемыми стенками, и находится под действием равномерно распределенной нагрузки q, приложенной на участке (–a,a) его поверхности.
Тогда решение этой задачи в безразмерных координатах сводится к определению непрерывной функции P(M,t), удовлетворяющей в области 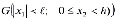 уравнению
уравнению
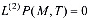 (22)
(22)
начальным
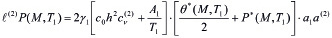 , (23)
, (23)
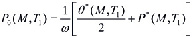 (24)
(24)
и граничным
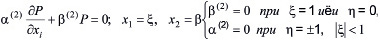 (25)
(25)
условиям, соответствующим данной задаче. Здесь L(2) – дифференциальный оператор вида
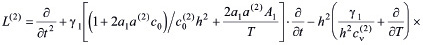
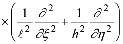 , (26)
, (26)
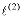 – оператор вида
– оператор вида
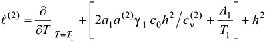
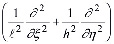 , (27)
, (27)
где
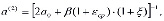
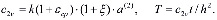
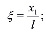
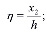
ξ, η – безразмерные координаты; с0 – предельное значение меры ползучести для уплотняемого грунта; А1 – параметр, зависящий от свойств и условий старения грунта;
Эти выражения получены из (14)-(21) при (9). Причем данная задача в одномерной постановке исследована в работе [11], а её решение, соответствующее начальному моменту времени получено в [7]. В то же время решения исследуемой задачи в различных постановках получены в [3-5]..
Данная краевая задача (22) - (27) в такой постановке дает возможность определить давление в поровой жидкости в безразмерных координатах. Начальное распределение порового давления для трехфазной среды имеет вид:
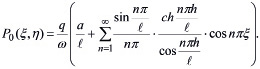 (28)
(28)
Решение уравнения (22), удовлетворяющее начальным (23),(28) и граничным (25) условиям получим в виде
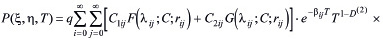
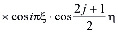 , (29)
, (29)
где
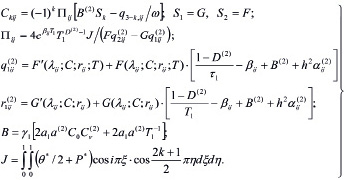 (30)
(30)
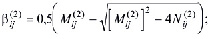
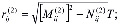
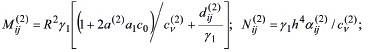
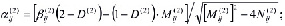
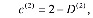
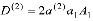 (31)
(31)
Здесь 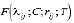 ,
,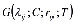 – вырожденные гипергеометрические функции первого и второго родов. При этом
– вырожденные гипергеометрические функции первого и второго родов. При этом 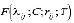 называется функцией Куммера. Она разлагается в степенной ряд, сходящийся при всех
называется функцией Куммера. Она разлагается в степенной ряд, сходящийся при всех 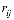 , т.е.
, т.е.
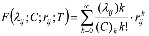 , (32)
, (32)
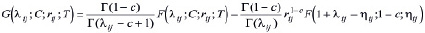
Используя соотношение 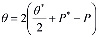 , сумму главных напряжений представим в виде
, сумму главных напряжений представим в виде
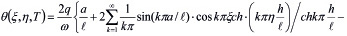
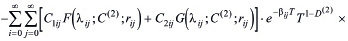
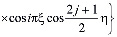 , (33)
, (33)
где 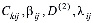 находятся из (30) и (31).
находятся из (30) и (31).
Тогда осадку уплотняемого слоя грунта определим по формуле
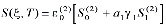 , (34)
, (34)
где
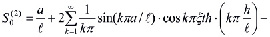
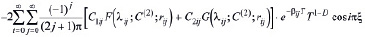 (35)
(35)
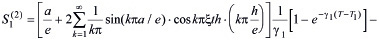
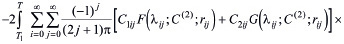
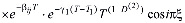 . (36)
. (36)
Таким образом, задача консолидации трехфазного грунта с учетом линейной ползучести и старения скелета можно сказать, что полностью решена для равномерно распределенной уплотняющей нагрузки.
В полученных решениях скорость консолидации зависит от безразмерных параметров 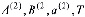 , которые в свою очередь зависят от параметров
, которые в свою очередь зависят от параметров 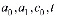 , определяемые по результатам компрессионных испытаний грунтов, которые для различных глинистых пород в основном имеются.
, определяемые по результатам компрессионных испытаний грунтов, которые для различных глинистых пород в основном имеются.
Используя выражения (29)-(36), вычислены давление в поровой жидкости и осадок уплотняемого слоя трехфазного грунта в зависимости от времени и пространственных координат. Анализ этих вычислений показывает, что развитие порового давления во времени имеет экстремальный характер, а осадка по времени после полного рассеивания порового давления продолжается пропорционально логарифму времени. Одновременный учет старения и ползучести скелета грунта снижает величину порового давления в процессе консолидации. Увеличивает величину начальной осадки и замедляет скорость протекания осадки по сравнению с фильтрационной теорией уплотнения земляных масс. При этом продолжительность протекания осадки по сравнению с фильтрационной теорией сокращается.
Библиографическая ссылка
Дасибеков А., Юнусов А.А., Юнусова А.А., Мадияров Н.К. МНОГОМЕРНЫЕ ЗАДАЧИ КОНСОЛИДАЦИИ НАСЛЕДСТВЕННО-СТАРЕЮЩИХ ЗЕМЛЯНЫХ МАСС // Международный журнал экспериментального образования. 2014. № 8-1. С. 37-46;URL: https://expeducation.ru/ru/article/view?id=5787 (дата обращения: 08.03.2026).

