В теории проверки статистических гипотез используются различные критерии оптимальности при выборе правила решения относительно принятия той или иной из гипотез.
Теорема Байеса в терминах плотностей устанавливает связь между апостериорной f(x|H) и априорной f(x|H) плотностями гипотезы H:
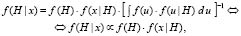
где x – вектор значений случайного вектора X; f(H) – априорная плотность гипотезы H; µ – символ пропорциональности. В математической статистике плотность f(x|H) принято называть сопряженной относительно плотности f(x|H).
Четкий байесовский тест
без функции потерь [1]
Пусть в простейшем случае имеются две
четкие гипотезы H0 и H1. Для принятия одной из них производятся измерения (эксперимент), в результате которых появляется вектор x = (x1, …, xn) измерений. Полагается, что компоненты Xi,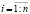 
случайного вектора
X = (X1, …, Xn) независимы и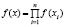 
,
где f(·) – заданная плотность распределения. В соответствии с теоремой
Байеса имеем:
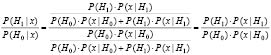
Так как априорные вероятности P(x|Hi) выражаются через соответствующие плотности f(x|Hi) : P(x|Hi) = f(x|Hi) dx1 ... dxn, поэтому (2) приводится к виду:
,
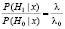где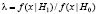 
– четкое отношение правдоподобия; 
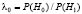– порог; P(Hi), i = 0, 1 – априорные вероятности появления, соответственно, гипотез H0, H1.
В соответствии с (2) возможны следующие ситуации:
если
,
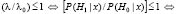
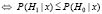тогда принимается гипотеза H0, т.е.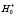
и, соответственно, отвергается H1, т.е. 
;
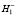если
,
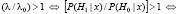
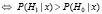тогда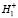 
и, соответственно, 
.
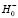Нечеткие апостериорные
распределения [3, 4]
Ниже теорема Байеса в формулировке (1) обобщается на случай нечетких данных и нечетких параметров априорных распределений. Обобщение основано на принципе расширения [15], с помощью которого находится нечеткий образ для нечеткого аргумента при воздействии нечеткого отображения. В этой задаче нечеткие данные и параметры, заданные соответствующими функциями принадлежностей, представляются в эквивалентной уровневой форме. Такое представление позволяет нечеткое апостериорное распределение интерпретировать как семейство четких распределений.
Случай 1. Экспериментальные данные – нечеткие, параметры априорных распределений – четкие.
Задача формулируется в следующем виде. Имеется теорема Байеса в ненормализованной форме (1):
.
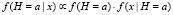Полагается, что случайный вектор
X = (X1, …, Xn) имеет независимые компоненты, а вектор измерений x = (x1, …, xn) имеет нечеткие компоненты xi,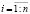 
с заданными функциями принадлежностей mi(x), x ∈ R1. Предполагается, что вектор параметров a = (a1, …, an) имеет четкие компоненты, т.е. 
, 
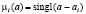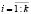. В этих условиях необходимо построить нечеткую апостериорную плотность:
.
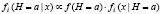Решение сформулированной задачи демонстрируется на примерах, приведенных ниже.
Библиографическая ссылка
Мочалов И.А., Шихаб Еддин М.Я. НЕЧЕТКИЕ БАЙЕСОВСКИЕ ТЕСТЫ // Международный журнал экспериментального образования. – 2014. – № 8-2. – С. 83-84;URL: https://expeducation.ru/ru/article/view?id=5892 (дата обращения: 25.04.2024).