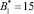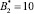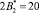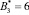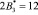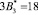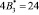Применение параллельных алгоритмов вычислений обусловлено высокими требованиями, предъявляемыми к скорости обработки информации. При этом обеспечение реального масштаба времени при вычислениях приводит к значительному усложнению аппаратуры, что в конечном итоге приводит к увеличению вероятности возникновения отказов. Применение модулярных кодов позволяет не только достичь высокой скорости обработки данных, но и обеспечить вычислительному устройству свойство отказоустойчивости. Для этого используются избыточные модулярные коды.
Модулярные коды относятся к кодам, которые используются для вычислений. Малоразрядность обрабатываемых остатков позволяет осуществлять вычисления в реальном масштабе времени параллельно и независимо по вычислительным каналам, определяемыми основаниями кода. В настоящее время широкое распространение получили коды системы остаточных классов (СОК) и коды полиномиальной системы классов вычетов (ПСКВ) [1–4]. Основное различие между данными кодами состоит в том, что в качестве оснований в СОК используются взаимно простые числа, а кодах ПСКВ – неприводимые полиномы.
Так как данные коды относятся к непозиционным кодам, то в основу алгоритмов поиска и коррекции ошибок в модулярных кодах положена процедура вычисления позиционной характеристики [5–10]. В основу данного подхода положено некоторое функциональное отношение, позволяющее однозначно отражать множество значений модульных характеристик на множество рассматриваемых ошибок Е. При этом следует обеспечить, чтобы математическая модель, описывающее данное отношение, при реализации обеспечивала бы параллельную организацию вычислений. Так в работе [5] в качестве позиционной характеристики, которую используют для коррекции ошибок в модулярном коде выступают старшие коэффициенты обобщенной полиадической системы (ОПС). В работе [6] представлен алгоритм вычисления позиционной характеристики интервал. В работе [7] доказаны теоремы, позволяющие использовать для коррекции ошибки в модулярном коде нормированный след полинома. В работе [8] для повышения скорости вычисления коэффициентов ОПС предлагается использовать ортогональные базисы безизбыточной системы.
В работах [5, 6] предлагается для проведения операции поиска и коррекции однократной ошибки в коде СОК, задаваемом рабочими основаниями p1, p2,... pk, использовать два контрольных основания, которые бы удовлетворяли условию
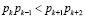, (1)
где k – количество рабочих оснований;
Однако упрочение контрольного основания требует значительного расширения диапазона обрабатываемых данных, поскольку специальным представлением (1) вводиться погрешность. А чтобы точность представления не претерпела заметного уменьшения, надо увеличивать диапазон представления величин, и тогда их истинные (без введенной погрешности) значения будут в пределах заданного рабочего диапазона.
Альтернативным путем решения данной проблемы является метод определения правильности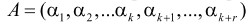 
на основе вычисления следа числа, которое представляет собой переход от исходного модулярного кода к коду вида
,
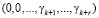при помощи преобразований, при которых не имеет место ни один выход за пределы рабочего диапазона системы.
Согласно [5] алгоритм вычисления следа числа заключается в последовательном вычитании из исходного модулярного кода, некоторых минимальных чисел, представленных в коде СОК. Эти числа называются константами нулевизации, при этом модулярный код числа А последовательно преобразуется к виду
,
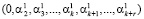затем в полином (0, 0,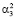 
,..., 
,..., 
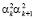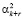и так далее. Осуществляя данную процедуру в течение k итераций, получается след числа
.
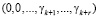Применение классического алгоритма вычисления следа числа позволяет последовательно получать наименьшее число, которое будет кратным сначала p1, затем число – кратное произведению p1, p2, и в конечном итоге – кратный рабочему диапазону, определяемому выражением
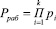. (2)
Основным недостатком данного алгоритма вычисления следа числа является последовательный характер вычислительного процесса, что не позволяет реализовать его на основе двухслойной нейронной сети. Это обусловлено прежде всего тем, что константы нулевизации представляют собой наименьшие возможные числа вида
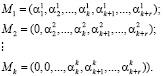(3)
где
.
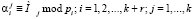Чтобы применить разработанный параллельный алгоритм вычисления следа числа необходимо заменить константы нулевизации Mi на псевдоортогональные числа. К таким числам относятся ортогональные базисы, у которых нарушена ортогональность по контрольным основаниям. Если положить условие, что число не содержит ошибок, то есть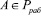 
, то это число модно представить в модулярном коде следующим образом
.
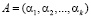Тогда, согласно китайской теореме об остатках (КТО), данное число A можно представить в виде
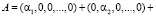
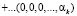. (4)
При этом каждое слагаемое выражения (4) можно представить, используя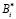 
– ортогональный базис безизбыточной системы оснований, в виде
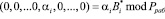, (5)
Проведем расширение системы рабочих оснований p1, p2,... pk на r контрольных pk+1, pk+2,... pk+r,. Используя полный набор из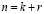 
оснований, представим 
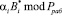в виде
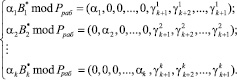(6)
Подставим выражения (6) в равенство (4). В результате получаем равенство
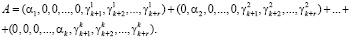(7)
Следовательно,
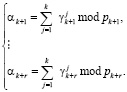(8)
Но при использовании китайской теоремы об остатках для перехода от модулярного кода к позиционному виду числа происходит выход за пределы рабочего диапазона.
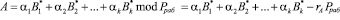, (9)
где rA – ранг числа А.
Следовательно, для получения правильного результата при вычислении следа числа необходимо учитывать значение ранга числа А. Значит, значение позиционной характеристики след числа определяется согласно
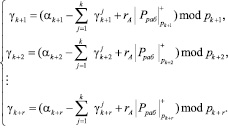(10)
Пусть задана упорядоченная СОК с рабочими основаниями р1 = 2, р2 = 3, р3 = 5. В качестве контрольных оснований выберем основания р4 = 7 и р5 = 11. Определим все псевдоортогональные числа, учитывая невозможность выхода за пределы рабочего диапазона Pраб(z) = 30. Полученные значения представлены в табл. 1.
Таблица 1
Псевдоортогональные числа СОК
|
Основание СОК |
Псевдоортогональный базис |
Код псевдоортогонального числа |
|
р1 = 2 |
|
(1, 0, 0, 1, 4) |
|
р2 = 3 |
|
(0, 1, 0, 3, 10) |
|
|
(0, 2, 0, 6, 9) |
|
|
р3 = 5 |
|
(0, 0, 1, 6, 6) |
|
|
(0, 0, 2, 5, 1) |
|
|
|
(0, 0, 3, 4, 7) |
|
|
|
(0, 0, 4, 3, 2) |
Так как новые константы нулевизации подобраны таким образом, что в процессе вычитания из исходного числа A выход за пределы рабочего диапазона не осуществляется, то по результату (10) можно судить о правильности кодовой комбинации СОК. Если система равенств (10) обращается в ноль, то исходный модулярный код не содержит ошибки, в противном случае – кодовая комбинация СОК является ошибочным. В табл. 2 представлены значения вектора ошибки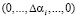 
для различных значений ошибки в коде СОК.
Таблица 2
Значения вектора ошибки модулярного кода СОК
|
Основание ПСКВ |
Значение вектора ошибки |
|
|
γ4(z) |
γ5(z) |
|
|
0 |
0 |
(0, 0, 0) |
|
1 |
4 |
(1, 0, 0) |
|
3 |
10 |
(0, 1, 0) |
|
6 |
9 |
(0, 2, 0) |
|
6 |
6 |
(0, 0, 1) |
|
5 |
1 |
(0, 0, 2,) |
|
4 |
7 |
(0, 0, 3) |
|
3 |
2 |
(0, 0, 4) |
Применение в качестве констант нулевизации псевдоортогональных базисов позволяет перейти от последовательной реализации алгоритма вычисления следа числа к параллельной. В связи с этим открываются дополнительные возможности по сокращению временных затрат на реализации процесса определения местоположения ошибки и ее глубины.
Рассмотрим пример применения параллельного алгоритма вычисления следа числа. Пусть задано число А = 29, которое принадлежит рабочему диапазону. Тогда в коде СОК данное число имеет вид А = (1, 2, 4, 1, 7). Произведем вычисление следа числа. Согласно КТО ранг данного числа равен rA = 1.
Для остатка α1 = 1 значение псевдоортогонального базиса имеет вид (1, 0, 0, 1, 4).
Для остатка α2 = 1 значение псевдоортогонального базиса имеет вид (0, 2, 0, 6, 9).
Для остатка α3 = 1 значение псевдоортогонального базиса имеет вид (0, 0, 4, 3, 2).
Значение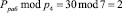 
.
Тогда значение следа согласно (10) имеет вид
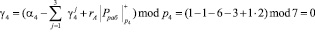
Вычислим значение следа по второму контрольному основанию.
Значение Pрабmod p5 = 30 mod 11 = 8. Тогда значение следа согласно (10) имеет вид
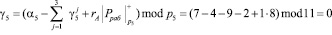
Таким образом, можно сделать вывод, о том, что код СОК А = (1, 2, 4, 1, 7) не содержит ошибки.
Пусть ошибка произошла по первому основанию и ее глубина равна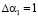 
. Тогда в код СОК имеет вид Аош = (0, 2, 4, 1, 7). Произведем вычисление следа числа. Согласно КТО ранг данного
числа равен rA = 1.
Для остатка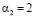 
значение псевдоортогонального базиса имеет вид (0, 2, 0, 6, 9).
Для остатка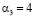 
значение псевдоортогонального базиса имеет вид (0, 0, 4, 3, 2).
Значение Pрабmod p4 = 30 mod 7 = 2.
Тогда значение следа согласно (10) имеет вид
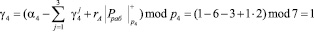
Вычислим значение следа по второму контрольному основанию.
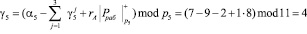
Так как позиционная характеристика отлична от нуля, то можно сделать вывод, о том, что код СОК А = (0, 2, 4, 1, 7) содержит ошибки. Согласно таблице 2 значение следа определяет, что ошибка по первому основанию, а ее глубина равна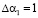 
. Тогда откорректированное значение кода равно А = (1, 2, 4, 1, 7).
Выводы
Для повышения скорости выполнения операции вычисления позиционной характеристики след числа был разработан параллельный алгоритм. С этой целью вместо классических констант нулевизации предложено использовать псевдоортогональные базисы. Проведенные исследования показали, что переход к параллельному алгоритму позволил сократить время вычисления позиционной характеристики при обработке 16-разрядных данных на 17,3 % по сравнению с классическим методом вычисления следа числа. Кроме того, применение параллельного алгоритма вычисления позиционной характеристики след числа позволил сократить аппаратурные затраты для реализации процедуры поиска и коррекции ошибки.
Библиографическая ссылка
Гапочкин А.В., Калмыков М.И., Айриян А.А. КОРРЕКЦИЯ ОШИБКИ В МОДУЛЯРНОМ КОДЕ НА ОСНОВЕ АЛГОРИТМА ПАРАЛЛЕЛЬНОГО ВЫЧИСЛЕНИЯ СЛЕДА // Международный журнал экспериментального образования. – 2014. – № 8-3. – С. 34-38;URL: https://expeducation.ru/ru/article/view?id=5926 (дата обращения: 22.12.2024).