Математические модели и их программная реализация сегодня широко используются в самых разнообразных областях, в том числе в биологии, экологии, эпидемиологии [1].
В докладе представлена программная реализация визуализации простейших моделей распространения эпидемий.
Важнейшая область применения моделей – это прогнозирование. В случае с эпидемиями это позволяет оценить возможную опасность от той или иной болезни и принять необходимые меры предосторожности. При моделировании реальной ситуации для решения задач прогнозирования можно идти двумя путями:
1. Рассчитать коэффициенты параметров модели, если они имеют физическое значение
2. Построить графики и подобрать параметры таким образом, чтобы модель соответствовала рассматриваемой ситуации.
Так как зачастую параметры модели выражают абстрактные коэффициенты, для которых нет четких формул расчета, чаще применяется второй подход.
Другая область применения математических моделей – обучение специалистов в прикладной области, поскольку визуализация позволяет наглядно показать в динамике, как влияет изменение разных параметров на конкретные моделируемые ситуации, что невозможно сделать при помощи мела и доски или статических презентаций. Это помогает лучше объяснить существующие взаимосвязи между параметрами и другими факторами. Для этой цели в работе реализованы в качестве примеров частные или типовые случаи выбора параметров, а также встроены обучающие упражнения на подбор тех или иных параметров модели для достижения определенных целей.
Модель Кермака-МакКендрика [2] представлена следующей системой дифференциальных уравнений:
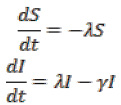 (1)
(1)
![]()
здесь S(t) – здоровые особи, которые находятся в зоне риска и могут быть инфицированы, I(t) – инфицированные особи, R(t) – особи, которые больше не распространяют вирус (это могут быть как выздоровевшие, так и погибшие), λ – так называемая сила инфекции, 1/γ – среднее время, в течение которого проходит болезнь.
Для этой модели в качестве частного случая моделируется эпидемия лихорадки Эбола в Новой Гвинее в 2014 году на период с марта до конца октября. Программа строит графики, полученные с помощью модели, которые соответствуют известным статистическим данным [3].
Рассмотрим модель эпидемии с бессимптомным протеканием болезни [4], где S(t) – число восприимчивых к вирусу людей, E(t) – число невакцинированных людей, I(t) – число инфицированных людей с симптомами, A(t) – число инфицированных людей без симптомов, H(t) – число госпитализированных людей, R(t) – люди, которые больше не распространяют инфекцию.
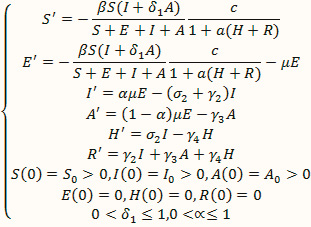 (2)
(2)
Описание параметров: β – коэффициент передачи при контакте, δ1 – коэффициент заражения без симпотомов (0;1], с – коэффициент передачи при контакте при отсутствии вспышки, a – коэффициент скорости госпитализации, μ – коэффициент прогрессирования передачи, α – группа зараженных из группы риска (0;1], σ2 – коэффициент выздоровления зараженных, γ2 – коэффициент выздоровления зараженных, γ3 – коэффициент выздоровления зараженных без симптомов, γ4 – коэффициент выздоровления госпитализированных.
1. Бессимптомная эпидемия
2. Локальная вспышка
3. Агрессивная эпидемия
4. Массовая эпидемия.
Визуализация решения системы уравнений позволяет наглядно показать в динамике, как влияет изменение вышеуказанных параметров на конкретные варианты распространения эпидемии.
Библиографическая ссылка
Ижуткин В.С., Сёмин П.Н. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ РАСПРОСТРАНЕНИЯ ЭПИДЕМИЙ // Международный журнал экспериментального образования. 2015. № 2-1. С. 32-33;URL: https://expeducation.ru/ru/article/view?id=6403 (дата обращения: 08.01.2026).

