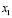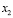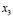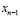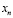Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Тимошенко Л.И. 1

---

1 Ставропольский филиал Краснодарского университета МВД России

Повышенный интерес к нейроподобным вычислительным системам обоснован прежде всего тем, что любые задачи должны решаться более эффективно при использовании нейросетевого логического базиса. В этом случае логический базис задачи определяет основной набор операций, реализуемых в процессе детализации алгоритма. Анализ показал, что в основном нейронные сети эффективны для решения так называемых трудноформализуемых и неформализуемых задач, связанных с необходимостью включения в алгоритм решения задач процесса обучения на реальном экспериментальном материале.

Статья в формате PDF

2122 KB

базовая операция

разработка высокоскоростного устройства

нейросетевая модель

сумматор по модулю два

скорость обработки

1. Адошев А.И., Аникуев С.В., Гальвас А.В., Жданов В.Г., Ивашина А.В., Кобозев В.А., Логачева Е.А., Привалов Е.Е., Тимошенко Л.И., Шарипов И.К. Современные технологии в образовании // Развитие системы образования – обеспечение будущего. – Одесса. – 2013. – С. 60-97.

2. Адошев А.И., Аникуев С.В., Тимошенко Л.И. и др. Развитие системы образования – обеспечение будущего. – Одесса. – 2013. – Том 1. – Книга 2.

3. Земцев А.М., Тимошенко Л.И. Информационная составляющая безопасной эксплуатации электроустановок // Методы и средства повышения эффективности технологических процессов в АПК: Опыт, проблемы и перспективы. – 2013. – С. 76-78.

4. Калмыков И.А., Тимошенко Л.И. Нейросетевые модели многовходовых сумматоров по модулю два // Фундаментальные исследования. – 2008. – № 3. – С. 73-74.

5. Калмыков И.А., Тимошенко Л.И. Систолическая матрица для цифровой фильтрации в модулярной арифметике // Современные наукоемкие технологии. – 2007. – № 11. – С. 98-100.

6. Калмыков И.А., Хайватов А.Б., Тимошенко Л.И., Гахов В.Р. Применение полиномиальной системы классов вычетов для повышения скорости функционирования спецпроцессора адаптивных средств защиты информации // Успехи современного естествознания. – 2007. – № 5. – С. 76.

7. Калмыков И.А., Зиновьев А.В., Тимошенко Л.И., Оленева Д.А. Математические модели цифровой обработки сигналов, используемые в современных информационных технологиях систем управления // Успехи современного естествознания. – 2009. – № 4. – С. 38-39.

8. Калмыков И.А., Емарлукова Я.В., Тимошенко Л.И., Гахов В.Р. Обобщенное дискретное преобразование Фурье для колец неприводимых полиномов // Успехи современного естествознания. – 2007. – № 5. – С. 77.

9. Калмыков И.А., Петлеваный С.В., Тимошенко Л.И., Лисицын А.В. Разработка преобразователя модулярного кода ПСКВ в позиционный код // Современные наукоемкие технологии. – 2006. – № 4. – С. 57-59.

10. Калмыков И.А., Тимошенко Л.И., Чипига А.А. Разработка преобразователя позиционного кода в полиномиальную систему класса вычетов // Современные наукоемкие технологии. – 2006. – № 4. – С. 59-60.

11. Кузьменко И.П., Тимошенко Л.И. Систолические принципы организации вычислений в спецпроцессоре цифровой обработки сигналов с параллельно-конвейерным распределением вычислительного процесса // Культура и общество: история и современность: материалы II Всероссийской (с международным участием) научно-практической конференции. – Ставрополь. – 2013. – С. 76-78.

12. Тимошенко Л.И. Нейросетевая реализация вычислений в полиномиальной системе классов вычетов // Фундаментальные исследования. – 2008. – № 3. – С. 71-73.

13. Тимошенко Л.И. Информатика. Курс лекций: Учебное пособие / Филиал РГСУ в г. Ставрополе. – Ставрополь. – 2014. – Том Часть 2.

14. Тимошенко Л.И. Анализ основных методов прямого преобразования из позиционной системы счисления в модулярный полиномиальный код // Современные наукоемкие технологии. – 2007. – № 9. – С. 23–24.

15. Тимошенко Л.И. Применение математической модели обладающей свойством кольца, для реализации цифровой обработки сигналов // Современные наукоемкие технологии. – 2007. – № 9. – С. 22-23.

16. Тимошенко Л.И. Реализация модульных операций в кольце полиномов с помощью нейронных сетей // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 1-1. – С. 22–25.

В последнее время наблюдается тенденция, когда нейронные сети стали использоваться при решении задач с ярко выраженным параллелизмом. К ним относятся задачи связанные с цифровой обработкой сигналов и изображений в реальном масштабе времени. Для этих задач переход к нейросетевому логическому базису обусловлен резким увеличением размерности пространства решения и необходимостью резкого уменьшения времени решения [1, с. 60-97; 2].

Для эффективной реализации математических моделей ЦОС определённых в кольце полиномов необходимо, чтобы вычислительные устройства могли эффективно поддерживать арифметические операции этой алгебраической системы. Рассмотрим выполнение таких операций в полиномиальной системе классов вычетов. Для этого необходимо представить значения остатков операндов в виде полиномиальной записи. Пусть степень неприводимого полинома

.

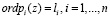Тогда справедливо

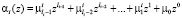. (1)

Аналогичным образом представим второй операнд

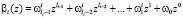. (2)

Известно [4, c. 73-74; 5, c. 98-100; 6, c. 76; 16, с. 22-25], что сравнения по одному и тому же модулю можно почленно складывать, то для суммы двух полиномов A(z) и B(z), имеющих соответственно коды 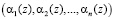и 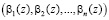справедливо соотношение:

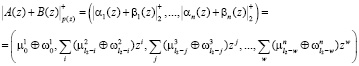, (3)

где 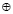– операция суммирования по модулю р.

Исходя из условия, что характеристика поля равна двум, то операция обратная суммированию выполняется аналогичным образом

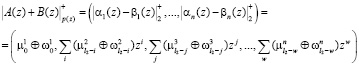. (4)

В результате выполнения (3) и (4) получаются элементы образующие циклическую группу по операции сложения. Для реализации операции сложения 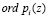-разрядных операторов в поле 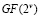по основанию .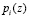. потребуется всего 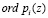двухвходовых сумматоров по модулю два. Причём базовая операция – сложение, реализуется за одну операцию и не требует применения итеративных методов построение НС конечного кольца, используемого в СОК [12, c. 71-73; 13; 14, c. 23-24].

Известно [7, c. 38-39; 15, c. 22-23], что в силу дистрибутивности операции умножения операндов над кольцом на элементы этого кольца относительно операции сложения имеем

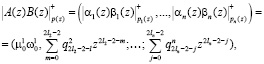(5)

где 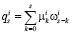– линейная свертка; ; .

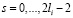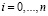Таким образом, выполнение операции умножения над операндами в кольце полиномов имеет вид

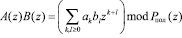, (6)

Из выражений (4) и (5) наглядно видно, что реализация модульного умножения реализуется на основе умножения соответствующих остатков по основаниям pi(z) с последующих суммированием по модулю характеристики поля. Следовательно, разработка высокоскоростного устройства, реализующего базовую операция по модулю характеристики поля в нейросетевом базисе, позволит обеспечить эффективную работу в реальном масштабе времени всего СП ЦОС.

Характерной чертой рассмотренных выше арифметических устройств, реализующих операции конечных алгебраических систем является наличие многовходовых сумматоров по модулю два. Исходя из данной структурной особенности, можно сформулировать основные требования к нейронной сети, выполняющей эту базовую операцию:

– использование параллелизма, причем распараллеливание должно производится на уровне побитовой обработки входного вектора;

– применение конвейерной организации вычисления;

– отказ от принципа рекуррентной редукции, от обратных связях в структуре НС конечного кольца;

– количество итераций в процессе выполнения операции должно быть минимальным;

– количество нейронов в слоях НС должно быть минимальным, обеспечивая требуемую скорость обработки входного вектора.

Результаты операции сложения по модулю два и значения входного вектора x определены на множестве {0,1}. Согласно [9, c. 57-59; 10, c. 59-60 ] операцию сложения по модулю два можно представить через совершенную дизъюнктивную или совершенную конъюнктивную нормальную форму. Это можно сделать при помощи таблицы функции (сложение по модулю два) f от n переменных (таблица). В последней строке таблицы 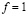если n – нечетно, 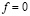если n – четно.

Определение функции сложения по модулю два n переменных

Используя правила построения совершенной дизъюнктивной нормальной формы, данную функцию можно записать

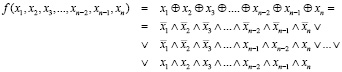(7)

для n – нечетного,

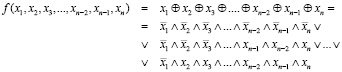(8)

для n – четного.

При помощи правил построения конъюнктивной нормальной формы получится

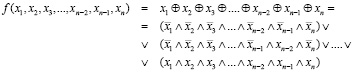
для n – нечетного,

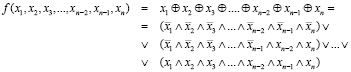(9)

для n – четного.

Из выражений (6-9) следует, что для нейросетевой реализации многовходового сумматора по модулю два можно использовать уже известные нейросетевые реализации логических функций И, ИЛИ, НЕ, описанные в [3, c. 76-78; 7, c. 38-39; 15, c. 22-23], которые при объединении в общую модель будут представлять собой структуру со следующими параметрами:

1. Число слоёв N=3. Первый распределяет значения входного вектора, второй производит вычисления дизъюнкции или конъюнкции, а третий объединяет полученные во втором слое значения при помощи конъюнкции или дизъюнкции.

2. Число нейронов первого слоя 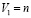, второго 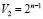, третьего 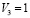. Таким образом, общее число нейронов для этой нейросетевой модели можно записать как .

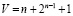Обладая минимальным числом слоев, эта нейросетевая модель сумматора по модулю два требует значительных аппаратурных затрат, зависимость которых от длины входного вектора выражена в виде степенной функции, что негативно сказывается на надежности устройства.

Библиографическая ссылка