В сыпучем продукте (жом, пивная дробина, сафлор и т.п.) обычно содержатся частицы, обладающие различными размерами, причем колебания в размерах частиц происходит в более широких пределах, чем колебания плотности.
Эксперименты показывают, что при вращении наклонного барабана частицы с меньшими размерами располагаются ближе к центру барабана и продвигаются через барабан медленнее, а частицы с большими размерами располагаются ближе к внутренней поверхности барабана и продвигаются через барабан быстрее. Вследствие различий в размерах и форме частиц сыпучего продукта, поверхность сползающего слоя шероховата. Мелкие частицы попадают во впадины этой поверхности и переходят в поднимающийся слой раньше, чем успевают достичь точки В на рис. 1.
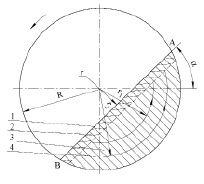
Рис. 1. Поперечное сечение барабана без внутренних насадок
При медленном вращении барабана поверхность слоя 1 располагается под углом естественного откоса Q. В том случае, когда угол наклона поверхности АВ a > Q частицы начинают осыпаться, образуя два слоя: сползающий r, в котором частицы подвижны относительно друг друга и барабана, и поднимающийся 3, в котором частицы движутся по концентрическим окружностям 4 и неподвижны относительно друг друга и барабана.
Если свободная поверхность продукта в барабане не параллельна горизонтальной прямой, то частица, двигаясь вниз в сползающем слое, проходит некоторое расстояние в осевом направлении, причем длина пути частицы в этом направлении прямо пропорциональна длине пути в сползающем слое. Данная схема движения объясняет явление осевого рассеивания частиц.
Крупные частицы находятся на поверхности сползающего слоя и при каждом скатывании проходят отрезок АВ. Вследствие самосортирования частиц в зависимости от их размеров, барабанные смесители непригодны для смешивания компонентов, размеры которых значительно отличаются.
Для количественной оценки неравномерности продвижения частиц через наклонный барабан в зависимости от различия в размерах частиц необходимо определить функциональную зависимость:
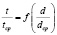 . (1)
. (1)
t – время продвижения частиц через барабан каждой, с; tср – среднее время продвижения частиц сыпучего продукта через барабан, с; d – диаметр частицы, м; dср – средний диаметр частиц основной массы сыпучего продукта, м.
Экспериментальным путем определена эта зависимость. Эксперименты проводились на лабораторной установке по той же методике, что и определение неравномерности продвижения частиц через наклонный барабан в зависимости от различия в их плотности.
В поток сыпучего продукта, находящегося в барабане, вводились меченые частицы с различными размерами. Плотность и форма меченых частиц были такими же, как плотность и форма частиц основной массы продукта.
На рис. 2 представлена зависимость времени продвижения частиц через наклонный барабан от их размеров. Как видно из рис. 2, размеры частиц оказывают существенное влияние на время пребывания их в барабане. Например, для частицы, диаметр которой в два раза меньше диаметра частиц основной массы продукта, время пребывания в барабане увеличивается в 4 раза.
Результаты экспериментальных измерений обработаны по способу наименьших квадратов, и получено следующее уравнение:
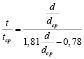 . (2)
. (2)
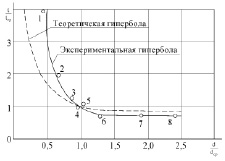
Рис. 2. График зависимости времени продвижения частиц через барабан от их размеров
Уравнение (2) представляет собой уравнение гиперболы. Обозначив коэффициент неравномерности продвижения частиц от различия в размерах частиц через εd, получим:
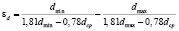 . (3)
. (3)
где tmax и tmin – соответственно максимальное и минимальное время пребывания в барабане отдельных частиц сыпучего продукта
Исходя из условий, что между размерами частиц и временем их пребывания в барабане существует гиперболическая зависимость, уравнение, подобное (2), может быть получено аналитически.
Библиографическая ссылка
Антипов С.Т., Шахов С.В., Кузнецов И.В., Матеев Э.З., Мелихов В.А. ОПРЕДЕЛЕНИЕ ВРЕМЕНИ ПРЕБЫВАНИЯ ЧАСТИЦЫ В БАРАБАНЕ В ЗАВИСИМОСТИ ОТ ЕЕ РАЗМЕРА // Международный журнал экспериментального образования. 2015. № 3-1. С. 116-117;URL: https://expeducation.ru/ru/article/view?id=6729 (дата обращения: 28.02.2026).

