Для достижения желаемого эффекта по обеспечению вычислений при стандартной разрядной сетке процессора цифровой обработки сигналов (ЦОС) были предложены алгоритмы коротких сверток, основанные на специальных способах умножения номиналов, которые можно использовать в соответствии с китайской теоремой об остатках (КТО) для вычисления больших сверток, заменяя их на последовательность коротких. Данные методы составляют основу второй группы методов цифровой обработки сигналов [1, с. 60-97., 2].
Если исходные две последовательности дискретных отчетов х(nT) и u(nT) представить в виде полиномиальной формы, то операцию циклического свертывания можно свести к процедуре умножения этих полиномов.
При этом вычисления циклической свертки двух последовательностей х(nT) и u(nT) равной длины N, эквивалентного нахождению коэффициентов полинома y(z) согласно выражения
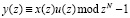, (1)
где х(z) и u(z) – полиномиальная форма последовательностей х(nT) и u(nT) соответственно.
Если положить, что двучлен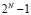 
может быть представлен в виде произведения S круговых неприводимых полиномов
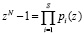, (2)
где S – число делителей N, то это позволяет использовать для вычисления коротких сверток КТО. В этом случае вычисление свертки (1) выполняется согласно алгоритма:
Приведение полиномов х(z) и u(z) по модулю pi(z), i=1, 2,…,S, т.е.
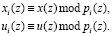(3)
2. Определение произведения
.
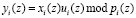Восстановление значений y(z) с помощью КТО, т.е.
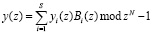. (4)
где Bi(z) – ортогональный базис i-го основания.
Если в качестве коэффициентов полиномов x(z) и u(z) выбрать элементы поля рациональных чисел Q, то рассматриваемый выше алгоритм будет иметь минимальную сложность. Это обусловлено тем, что в поле рациональных чисел круговые полиномы с индексами N<105 имеют простые коэффициенты {–1, 0, 1}
В этом случае обобщенная форма алгоритмов вычисления коротких сверток с помощью КТО имеет вид
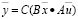, (5)
где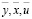 
– векторная форма выходной, входной и сворачивающей последовательностей соответственно; C, B, A, – матрицы; «·» – поточечное произведение векторов.
Значения элементов матриц C, B, A для коротких сверток длинной N <9, обеспечивающих минимальное количество операций умножения, приведены в работе [7, с. 76, 8, с. 38-39, 9, с. 77]. Альтернативным решением проблемы сокращения времени вычисления циклических сверток является гнездовой алгоритм.
Вычисление циклической свертки непосредственно по выражению (5) требует разработки специальных алгоритмов, минимизирующих число операций умножения для каждого значения N. Лучшие оценки по быстродействию вычислительных устройств получаются при использовании гнездового алгоритма [4, с. 60-97].
В основу данного алгоритма положена возможность сведения вычисления одномерной свертки к многомерной. Отправной точкой такого преобразования является изоморфизм, порождаемый китайской теоремой об остатках [5, с. 73-74, 14].
Если длина циклической свертки N может быть представлена в виде произведения двух чисел n1 и n2, т. е. N = n1 n2, причем НОД (n1, n2) = 1, то любое число из интервала 0, 1 … N–1 можно записать в виде (m1, m2), где m1 = N mod n1, m2= N mod n2. Тем самым устанавливается взаимнооднозначное соответствие между элементами кольца N и целыми числами отрезка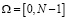 
. При этом вычет m1 рассматривается как первая координата числа N, а вычет m2 – как вторая координата.
Рассмотрим матричную форму представления операции циклической свертки. В этом случае выражение (1) имеет вид
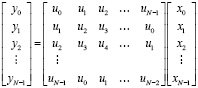. (6)
Тогда циклическая свертка определяется в виде произведения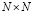 
циклической матрицы свертки на сворачиваемый вектор. Если строки матрицы упорядочить по первой координате m1, а столбцы – по второй, то получим разбиение по блокам, каждый из которых также образует циклическую матрицу для свертки меньшей размерности.
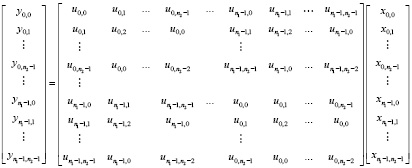
Перестановки строк и столбцов циклической матрицы осуществляются в следующем порядке: первыми ставятся те, у которых первая координата равна 0 , а вторая – в возрастающем порядке, затем те, у которых первая координата равна 1 и вторая в возрастающем порядке. В результате получается блочно-циклическая структура.
Обозначив через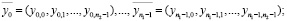 
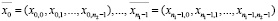, а также
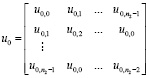
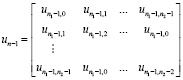
получаем преобразованную матрицу в более компактном виде
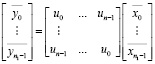. (7)
Для реализации гнездового алгоритма вычисления сверток представим выражение (7) в полиномиальной форме, воспользовавшись z-преобразованием. Тогда
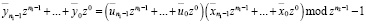. (8)
используя круговые полиномы pi(z) представим двучлен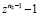 
в виде
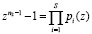. (9)
Тогда на основе КТО, получаем (1.28)
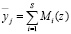, (10)
где
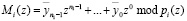. (11)
Известно [6, с. 98-100, 11, с. 59-60], что с помощью интерполяционной формулы Лагранжа может быть точно восстановлен полином степени N-1 по значениям N точках. В этом случае метод нахождения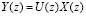 
заключается в определении констант <
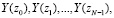а затем в вычислении интерполяционной формулы
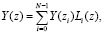(12)
в которой интерполяционные полиномы имеют вид
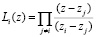. (13)
В общем случае сложность гнездового алгоритма определяется следующим образом. Если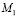 
и 
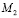– количество умножений в алгоритмах вычисления 
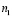и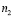 
– точечной сверток соответственно, а 
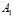и 
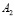– количество сложений. Тогда, при НОД 
, 
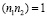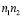– точечная свертка вычисляется за 
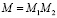операций умножений и 
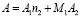сложений.
Перестановка местами первой и второй координаты обработки приводит к изменению количества операций сложений, которые составят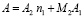 
. Таким образом, при выборе гнездового алгоритма предпочтение отдается тому способу при котором число сложений меньше.
Если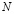 
разлагается в произведение более чем двух взаимно простых сомножителей 
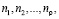то выражение для оценки временных затрат имеет вид
– число умножений
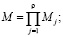(14)
– число сложений
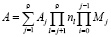(15)
при условии, что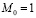 
.
В формуле (15) в каждом последующем слагаемом количество символов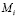 
увеличивается на единицу по сравнению с предыдущим, вследствие чего число операций сложений A гораздо сильнее зависит от числа операций умножения 
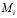, чем от числа сложений. Поэтому для больших сверток наиболее выгодны алгоритмы, вычисляющие короткие свертки с наименьшим числом умножений, даже если это достигается за счет увеличения числа операций сложения.
Применение гнездового алгоритма вычисления сверток позволяет осуществлять процедуры ортогональных преобразований сигналов, не используя тригонометрические функции. Отказ от быстрых алгоритмов ДПФ позволяет осуществлять переход от алгебраической системы, функционирующей в поле комплексных чисел в поле рациональных чисел Q(R).
В работах [17, с. 22-25, 12, с. 76-78] приведена нижняя оценка эффективности различных сверточных алгоритмов. Известно, что вычисление линейной свертки двух последовательностей х(n) и u(n) длины N эквивалентно определению коэффициентов полинома
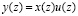. (16)
При этом ord y(z) = ord x(z) + ord и (z) = 2N – 2. Применение данного алгоритма позволяет найти значение x(zi), и u(zi) в точках zi, i = 0,1,…,2N – 2, с последующим вычислением произведения
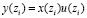. (17)
Искомый полином y(z) полностью определяется значениями yi(z) заданных в 2N-1 точках интерполяции zi. Таким образом, если для восстановления используется быстрый интерполяционный полином по китайской теореме об остатках, то вычислительная сложность алгоритма линейной свертки определяется 2N-1 умножениями вида (16).
В работах [13, с. 71-73, 18, с. 367-371, 19, с. 188-193 ] доказано, что минимальное число умножений, необходимых для вычисления циклической свертки длины N, равно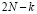 
, где k – число делителей N , включая 1 и N. Известно, что полином 
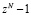разлагается на произведение круговых полиномов, число которых равно k. Если положить, что tj – делитель N, то соответствующий этому делителю круговой полином 
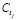имеет степень 
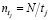, а сумма степеней круговых полиномов равна N.
Применение КТО позволяет свести вычисление циклической свертки к выражению
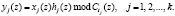(18)
Известно, что для реализации равенства (1.36.18) требуется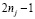 
умножений. Проведя суммирование по всем j, получаем
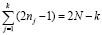. (19)
Таким образом, очевидно, что для сверток малой длины граница мультипликативной сложности достигнута, и, следовательно, улучшение алгоритмов цифровой обработки сигналов возможно только за счет сокращения числа операций сложения [15, с. 23-24, 16, с. 22-23].
Однако, несмотря на то, что все алгоритмы с минимальной мультипликативной сложностью имеют структуру вида (5), где поточечное умножение векторов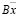 
и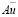 
требует выполнения 2N-1 итераций над операндами, практическая реализация их довольно сложна. Кроме того, изменение величины N входного вектора x(n) влечет за собой изменение всей структуры вычислительного устройства.
Обращаясь к рассмотренным алгоритмам можно легко заметить, что наибольший выигрыш от их применения возможен только при реализации на основе классической фон-неймановской архитектуры построения вычислительного устройства. Таким образом, обобщая сказанное, можно сделать вывод о том, что рассмотренные выше ортогональные преобразования, реализованные в поле комплексных чисел, быстрые алгоритмы их вычисления, а так же гнездовые вычисления сверток не позволяют в полной мере реализовать все достоинства представляемые нейросетевым базисом.
Вместе с тем существуют математические модели ЦОС, обладающие свойством конечного кольца и поля, которые характеризуются простой реализацией, высоким уровнем параллелизма и возможностью построения с использованием нейросетевого базиса. Среди таких моделей особое место занимают теоретико-числовые и полиномиальные преобразования в полях Галуа.
Библиографическая ссылка
Тимошенко Л.И. ПРИМЕНЕНИЕ БЫСТРЫХ СВЕРТОЧНЫХ АЛГОРИТМОВ // Международный журнал экспериментального образования. – 2015. – № 4-2. – С. 336-340;URL: https://expeducation.ru/ru/article/view?id=7367 (дата обращения: 18.04.2024).