На современном этапе развития электронных коммерческих систем электронные деньги находят все большее распространение. Такая ситуация определяется достоинства, которыми обладает электронная наличность. В то же самое время для эффективного функционирования систем электронных платежей (СЭП) необходимо разрабатывать и использовать протоколы, обеспечивающие обмен данными между покупателем и продавцом в реальном масштабе времени и с высокой степенью защиты от несанкционированного доступа (НСД) и модификации.
Очевидно, что одним из основных свойств любой системы безналичных расчетов является обеспечение безопасности всех ее компонентов на всех этапах функционирования этой системы. При этом покупатель, использующий электронную наличность (эмитент) и продавец (эквайер) должны быть уверены в защите своих вложений. К сожалению, всестороннее развитие Интернета и мобильной связи, как показал анализ, не позволяют в полной мере обеспечить требуемый уровень защиты данных. Поэтому разработка протоколов, обладающих высокой степенью защиты данных от несанкционированного доступа, является актуальной задачей.
Обеспечить высокую степень защиты от НСД передаваемых данных можно за счет применения различных алгоритмов шифрования. При этом для обеспечения интерактивного обмена данными между двумя сторонами, участвующими в работе СЭП, такие алгоритмы должны работать в реальном масштабе времени. Одним из решений данной проблемы является использование в системах электронной платежей поточных шифров, на основе псевдослучайных последовательностей (ПСП).
Однако процедура обеспечения конфиденциальности и целостности информации на основе сложения потока псевдослучайных битов с битами исходного текста по модулю два не отличается стойкостью и может быть раскрыта при наличии определенного количества символов исходного и шифрованного текста. Несмотря на то, что такой шифр считается теоретически нераспознаваем, то с помощью системы уравнений можно раскрыть структуру генератора ПСП, имея в наличии 2k символов открытого и зашифрованного текста, где k – степень порождающего полинома.
Одним из путей решения является использование нелинейных алгоритмов шифрования, которые реализуются с использованием непозиционных модулярных структур [1-4]. В данных алгоритмах нашли широкое применение операции сложения, умножения и возведения в степень элементов конечного поля, а также их комбинаций. Так в работе [5] с целью повышения скорости выполнения нелинейных операций предлагается перейти к использованию полиномиальной системы классов вычетов. Параллельная независимая обработка малоразрядных остатков позволяет повысить скорость базовых операций алгоритмов нелинейного шифрования. В работе [6] предлагается использовать индексное представление элементов конечного поля Галуа. Переход к индексам позволил заменить низкоскоростную операцию возведения в степень по модулю на операцию умножения индексов.
Однако использование криптографических преобразований целесообразно при закрытии передачи данных по открытому каналу связи между пользователями СЭП. В то же самое время в протоколе выплаты электронной наличности в прямом виде нельзя использовать процедуры нелинейного шифрования. Как правило, для обеспечения требуемого уровня защиты от НСД в таких протоколах применяются псевдослучайные функции (ПСФ). В работах [7-8] представлена псевдослучайная функция, которая при меньшей длине ключа обеспечивает высокую криптостойкость, которая соответствует сложности решения l-DDH проблемы. Применение данной псевдослучайной функции в системах электронных платежей приведено в работах [9,10]. Использование одной ПСФ в различных протоколах позволяет сократить объем памяти носителя электронного кошелька, который будет использоваться для хранения программного обеспечения.
Рассмотрим использование этой ПСФ в протоколе «выплаты одной монеты». Для организации протокола выплаты электронной наличности пользователь имеет два ключа – открытый Котк и секретный Ксекр. Открытый ключ применяется банком при выдаче электронного кошелька своему абоненту-покупателю. Секретный ключ покупателя Ксекр участвует в процессе выплаты электронных денег. Но при этом Ксекр должен быть в таком виде, чтобы продавец не смог его вычислитель самостоятельно.
В данной системе электронных платежей покупатель, будучи легальным пользователем системы, вычисляет свой открытый ключ согласно
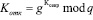, (1)
где q – порядок мультипликативной группы с порождающим элементом g.
Для осуществления процедуры выплаты у покупателя должен быть в наличии электронный кошелек W, который содержит секретный ключ владельца Ксекр, параметр S для генерации номера электронной купюры, параметр Т для проведения протокола «двойной выплаты»,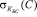 
– подпись банка на вручение С, которое использовал покупатель при получении кошелька в банке; КБС – секретный ключ банка; J – показатель счетчика электронных монет
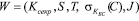. (2)
Для осуществления покупки владелец электронного кошелька обращается к продавцу. При этом он должен доказать последнему следующие, моменты:
– в кошельке W у него есть подпись банка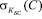 
на вручение С, т.е.
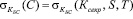; (3)
– покупатель правильно сгенерировал SJ номер J-й электронной купюры, используя при этом псевдослучайную функцию
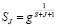. (4)
Рассмотрим более подробно каждый этап протокола «выплаты одной монеты». При обращении в банк за электронным кошельком, покупатель доказывал банку в протоколе «снятия электронных денег со счета», что он является авторизованным пользователем этой наличности. Для этого покупатель вычислял вручение согласно следующего равенства
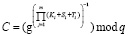, (5)
где Ki, Si и Ti – i-й блок, полученный при разбиении чисел секретного ключа Ксекр, параметров S и Т на m частей; g –порождающий элемент мультипликативной группы; q – порядок мультипликативной группы с порождающим элементом g.
Затем после проверки подлинности покупателя банк подписывает вручение C и передает свою подпись в электронном кошельке его владельцу.
На первом этапе покупки с помощью электронной наличности , для того чтобы доказать продавцу, что в электронном кошельке присутствует подпись банка, выдавшего электронные купюры, покупатель производит вычисление вручение
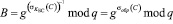, (6)
где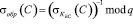 
– обратная величина подписи вручения банку.
Затем покупатель затемняет значение вручения банка
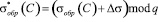, (7)
где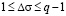 
– случайная величина.
После этого покупатель вычисляет затемненное вручение продавцу
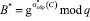. (8)
Эти значения пересылаются продавцу, который в ответ высылает случайное число, которое принадлежит мультипликативной группе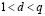 
. Владелец электронного кошелька, получив вопрос d, производит ответ на поставленный вопрос
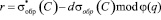. (9)
Далее покупатель передает ответ на поставленный вопрос продавцу. Затем продавец производит проверку полученного ответа
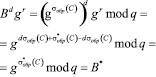(10)
Если выражение (10) будет истинным, то это свидетельствует о том, что покупатель обладает электронным кошельком, который подписан банком. Другими, словами, покупатель является платежеспособным.
Данную процедуру проверку наличия у покупателя электронного кошелька можно провести применяя другой алгоритм. В этом случае, используя свой секретный ключ, покупатель закрывает данные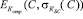 
и пересылает зашифрованный текст продавцу товара.
Продавец, зная открытый ключ покупателя, расшифровывает данное сообщение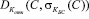 
и получает в открытом виде вручение С покупателя и подпись банка на это вручение 
.
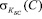После этого продавец обращается в банк и, получив его открытый ключ, расшифровывает его подпись. Результатом данной процедуры является вручение С, которое представил покупатель в банк для получения кошелька. Продавец сравнивает эти значения. При совпадении этих значений продавец убеждается, что у покупателя есть электронный кошелек.
Реализация последнего алгоритма возможна только в том случае, когда продавец может интерактивно обращаться в банк. При этом первый алгоритм проверки электронного кошелька у покупателя позволяет обеспечить автономную работу двух субъектов «купли-продажи», не увеличивая при этом трафик между банком и его клиентами.
Выводы
Использование в системах электронной коммерции криптографических протоколов аутентификации покупателя позволяет обеспечить высокую надежность работы такой системы. Применение разработанного протокола выплаты электронной наличности с использованием модулярной арифметики позволяет продавцу в интерактивном режиме провести проверку наличности покупателя. При этом применение единой псевдослучайной функции позволит сократить затраты на память в носителе электронного кошелька за счет использования ПСФ в нескольких протоколах.
Библиографическая ссылка
Топоркова Е.В., Калмыков М.И., Борода Н.П., Сирота С.А. РАЗРАБОТКА ПРОТОКОЛА ВЫПЛАТЫ ЭЛЕКТРОННОЙ НАЛИЧНОСТИ С ИСПОЛЬЗОВАНИЕМ МОДУЛЯРНОЙ АРИФМЕТИКИ // Международный журнал экспериментального образования. – 2015. – № 4-2. – С. 341-343;URL: https://expeducation.ru/ru/article/view?id=7368 (дата обращения: 21.11.2024).