Предлагаемая методическая разработка предназначена для студентов заочного обучения технологических специальностей. В работе рассматриваются основные теоретические положения по разделам «Дифференциальное исчисление функции многих переменных», «Дифференциальные уравнения» и «Теория вероятностей». Изложение необходимых теоретических сведений параллельно сопровождается решением типовых примеров и задач различной сложности. Приводятся также семестровые контрольные задания, даются методические рекомендации и подходы к их решению. Данная разработка может быть использована также студентами дневного обучения.
В главе 1 «Дифференциальное исчисление функции многих переменных» даются указания и рекомендации студенту-заочнику к выполнению контрольной работы по разделу «Дифференциальное исчисление функции многих переменных», а также приводятся контрольные задания. Параллельно по мере рассмотрения теоретических сведений изучите методические подходы к решению типовых задач. В целях приобретения практических навыков решения задач предварительно выполните предлагаемые упражнения по данной теме.
В главе 2 «Дифференциальные уравнения» рассматриваются необходимые теоретические сведения, а также излагаются методы решения ряда типовых задач, разбор которых окажет студенту-заочнику существенную методическую помощь при выполнении контрольной работы.
Напомним, что уравнения вида F(x, y, y′) = 0, где x – независимая переменная, y – искомая функция от x, y′ – ее производная, называется дифференциальным уравнением первого порядка. Если уравнение можно разрешить относительно y′, то оно принимает вид y′ = f(x, y) и называется уравнением первого порядка, разрешенным относительно производной. В некоторых случаях это уравнение удобно записать в виде
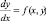
или в такой форме
f(x, y)dx – dy = 0,
являющимся частным случаем более общего уравнения
P(x, y)dx + G(x, y)dy = 0,
где P(x, y) и Q(x, y) – известные функции. Функция y = y(x), заданная на интервале (a, b), называется решением уравнения, если при подстановке в уравнение его обращает в тождество относительно x ∈ (a, b). График решения дифференциального уравнения называется интегральной кривой. Ответ на вопрос о том, при каких условиях уравнение имеет решение, дает теорема Коши. Поскольку эта теорема фундаментальная, поэтому сформулируем её.
Теорема Коши (существования и единственности решения).
Пусть правая часть f(x, y) уравнения y′ = f(x, y) определена в некоторой области D на плоскости OХY. Если существует такая окрестность Ω точки M0(x0, y0) области D, в которой f(x, y) удовлетворяет условиям:
1. Непрерывна по совокупности аргументов.
2. Имеет ограниченную частную производную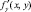 
, то существует единственное решение y = y(x) уравнения в некоторой окрестности точки x0, удовлетворяющее условию y0 = y(x0).
Геометрически это означает, что через данную точку проходит единственная интегральная кривая. Эта теорема имеет локальный характер, она гарантирует существование единственности решения уравнения лишь в достаточно малой окрестности точки x0. Из этой теоремы следует, что уравнение имеет бесконечное множество различных решений. Условие y0 = y(x0) называется начальным условием.
Отыскание решения уравнения, удовлетворяющего начальному условию, называется задачей Коши. С геометрической точки зрения решить задачу Коши означает: выделить из множества интегральных кривых ту, которая проходит через заданную точку.
При этом решение дифференциального уравнения первого порядка называется особым, если соответствующая интегральная кривая обладает тем свойством, что через каждую ее точку проходит, кроме нее, еще и другая касающаяся ее интегральная кривая данного уравнения.
Итак, особое решение представляет такое решение, в каждой точке которого нарушается единственность решения задачи Коши.
В главе 3 «Теория вероятностей» рассматриваются теоретические сведения и упражнения по основным разделам в этой области, также предлагаются контрольные задания для самостоятельного выполнения. При нахождении вероятностей в смысле классического определения широко используются комбинаторика. Пусть имеется множество x = {x1, x2, ..., xn} (n < ∞). Размещением из n элементов множества Х по k элементам называется упорядоченный набор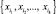 
элементов множества Х. Число всех размещений 
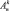(из n элементов по k) определяется формулой
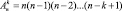
В частности, размещение из n элементов по n называется перестановкой; а число всех перестановок Pn вычисляется по формуле Pn = n!
Сочетанием из n элементов по k называется любое подмножество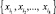 
, содержащее k элементов. Число всех сочетаний 
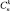(из n элементов по k) вычисляется по формуле
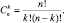
Библиографическая ссылка
Ильмушкин Г.М. МАТЕМАТИКА. УПРАЖНЕНИЯ И ЗАДАЧИ (УЧЕБНОЕ ПОСОБИЕ) // Международный журнал экспериментального образования. – 2015. – № 5-2. – С. 279-280;URL: https://expeducation.ru/ru/article/view?id=7641 (дата обращения: 19.04.2024).