Строительство сооружений на слабых глинистых грунтах требует более внимательного подхода к ним, чем к другим грунтам. Это связано с тем, что сооружения, взаимодействующие с такими грунтами, испытывают большие осадки. Причем они протекают в течение длительного времени. Это подтверждается плачевным состоянием многочисленных зданий г. Шымкента Южно-Казахстанской области и г. Чирчика Ташкентской области Республики Узбекистан. На таких водонасыщенных глинистых грунтах прежде чем строить высотные здания создают искусственные основания, применяя песчаные подушки мощностью от 1–2 м до 7 м. Они позволяют уменьшить глубину заложения фундаментов и увеличивают их устойчивость, а также применение их уменьшает осадки фундаментов. Кроме того, песчаные подушки используются в качестве дренирующего слоя, так как поровая вода из нижележащих глинистых грунтов отжимается в процессе уплотнения грунтов от веса самой подушки, ускоряя процесс консолидации грунтов основания.
Грунт в общем случае находится в сложном НДС, вызванном воздействием внешних нагрузок, передающихся через фундамент и силами собственного веса, т.е. имеет место пространственное сжатие грунта. Однако в инженерной практике часто создаются условия, когда такое состояние уплотняемого массива многокомпонентного грунта сводится к одномерной задаче. К таким случаям относятся уплотнения грунтовых массивов и слоев в основании сооружений, имеющих большие размеры по сравнению с их мощностью.
При одномерном уплотнении элементарный кубик, выделенный из массива грунта деформируется в условиях отсутствия бокового расширения. Причем направление сжимаемости кубика-образца совпадает с направлением действия наибольшего главного напряжения. В двух других направлениях деформации равны нулю. В этих условиях относительная деформация уплотнения равна относительной объемной деформации грунта.
Для выяснения общего характера протекания процесса уплотнения достаточно будет рассмотреть отдельные решения именно этой задачи, физическая сторона которой не очень отличается от аналогичных решений трехмерных задач. С другой стороны, исследования одномерного уплотнения более доступны, чем двух и трехмерных. Кроме того, это дает возможность при рассмотрении процесса уплотнения учесть некоторые факторы, сильно влияющие на него, в частности, можно указать на одновременный учет неоднородности, старения и ползучести уплотняемых грунтов. В связи с этим ниже исследуем процесс уплотнения, происходящий в слое трехфазного грунта для ряда задач механики.
Итак, рассмотрим уплотнение слоя грунта мощностью h, залегающего под песчаной подушкой. В начальный момент времени (t = 0) к слою грунта мгновенно прикладывается распределенная нагрузка с интенсивностью q = q (z, t). Верхняя поверхность уплотняемого массива водопроницаема, а нижняя водонепроницаемая. При этом величина избыточного порового давления p (z, t) при t = 0 будет равна
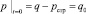, (1)
т.е. часть нагрузки, равная величине структурной прочности сжатия рстр, сразу же воспринимается скелетом грунта.
Основное уравнение одномерной задачи механики однородных уплотняемых трехфазных грунтов без учета ползучести имеет вид [1]
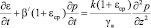, (2)
где ε – коэффициент пористости; b’ – коэффициент объёмного сжатия; k – коэффициент фильтрации; εср – средний коэффициент пористости; γв – объёмный вес воды; р – давление в поровой жидкости; t – время; z – координата.
Состояние скелета упругоползучего однородного грунта и уравнение равновесия, может быть соответственно математически описано следующим соотношением [4]:
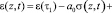
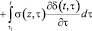, (3)
где
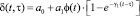, (4)
ε (τ1) – начальный коэффициент пористости; a0 – коэффициент сжимаемости;
σ(z, t) – напряжение в скелете грунта; τ1 – момент приложения нагрузки; a1, γ1 – параметры ползучести; φ(t) – функция старения.
Согласно общей модели В.А. Флорина [4] имеем:
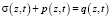, (5)
Рассматривая совместно выражения (1)–(4), после некоторых математических выкладок относительно порового давления, получим следующее дифференциальное уравнение в безразмерных координатах:
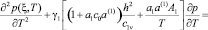
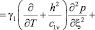
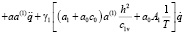, (6)
где
, 
, 
,
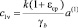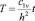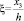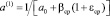. (7)
Начальными условиями для данной задачи будут:
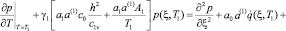
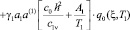, (8)
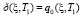, (9)
Уравнение вида (6) при постоянной нагрузке и без учета структурной прочности сжатия грунта исследовано в [5].
Если грунт деформируется только в вертикальном направлении, то по теории фильтрационной консолидации сумма избыточного порового давления и эффективного напряжения в грунте σ (z, t) в любой момент времени равна внешней нагрузке, т.е. p + σ = q.
При модифицированном законе Дарси граничные условия исследуемой задачи примут вид
, 
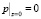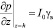. ( 10)
Здесь I0 – начальный градиент напора.
В выражениях (6)–(10) заменим функцию p (z, t) на
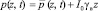, (11)
тогда соответственно получим:
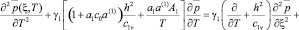
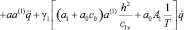, (12)
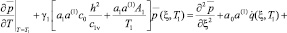
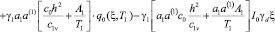, (13)
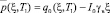, (14)
, 
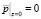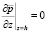. (15)
Таким образом, данную задачу можно сформулировать следующим образом. В безразмерных координатах требуется определить давление в поровой жидкости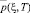 
, напряжение в скелете σ (ξ, T) и вертикальные перемещения верхней поверхности S(T) (осадок) грунтового слоя в области 
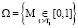, если 
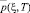удовлетворяет дифференциальному уравнению (12) начальным (13), (14) и граничным (15) условиям.
Решение уравнения (12), удовлетворяющее указанным условиям, представим в виде
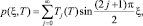
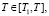
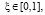(16)
где
, 
,
;
;
;
.
.
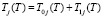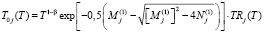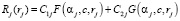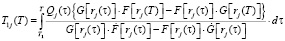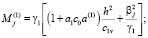
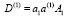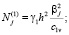
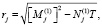
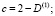
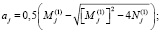
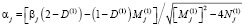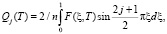
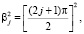
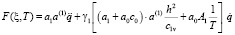Здесь F(aj, c, rj) и G(aj, c, rj) соответственно являются вырожденными гипергеометрическими функциями первого и второго родов. Коэффициенты Ckj k = 1,2 определены из начальных условий (13), (14). При этом F(aj, c, rj) называется функцией Куммера. Она разлагается в степенной ряд
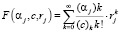. (17)
Тогда функция G(aj, c, rj) через F(aj, c, rj) выражается следующим образом:
.
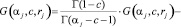
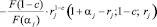Причем ряд (17) сходится при всех rj.
Для вычисления осадок S(T) грунта в безразмерной координате используем формулу вида
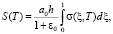(18)
где σ (ξ, T) – напряжение в скелете грунта.
Оно находится из
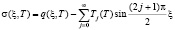. (19)
Подставив выражение (19) в (18), находим
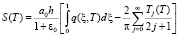. (20)
При Т → 0 имеем, что σ (ξ, T) → 0, а при Т → ∞ напряжение стремится к q. Следовательно, если поровое давление изменится от q до 0, то напряжение принимает значение от 0 до q. При этом S(T) изменится от 0 до
. (21)
Если q (ξ, T) = q = const то из (21) находим, что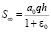 
, т.е. неустановившаяся осадка слоя уплотняемого грунта во времени изменяется в диапазонах от 0 до .
Анализ расчетных формул показал, что с увеличением мощности уплотняемого грунтового массива максимальное значение порового давления и время его наступления увеличивается. При этом значение осадки уменьшается в течение всего периода уплотнения. Так, например, при толщине слоя 5 и 20 м максимальное значение порового давления отличается более чем 1,5 раза. Причем для толщины 20 м пик более растянут по сравнению с пиком для толщин 5 и 10 м. Это означает, что с увеличением толщины уплотняемого слоя грунта уменьшается скорость нарастания напряжений в скелете грунта, а в уплотняемых грунтовых массивах с малыми мощностями скорость нарастания напряжений в скелете грунта не только велика, что приводит к отставанию роста деформаций от роста напряжений в скелете грунта. В то же время при большой толщине уплотняемого слоя грунта скорость нарастания напряжений в скелете грунта будет небольшой и деформации уплотнения вследствие ползучести и старения скелета грунта протекает без заметного отставания.
Таким образом, максимальное значение порового давления в основаниях сооружений зависит от длины пути фильтрации, т.е. от размеров уплотняемого слоя грунта. Причем чем больше мощность уплотняемого грунтового массива, тем медленнее протекает фильтрационные процессы. Это означает, что процесс возрастания порового давления будет продолжаться за счет ползучести и старения скелета грунта.
Следует заметить, что подобные задачи в иных постановках, авторами данной работы, также исследованы в [1–3].
Библиографическая ссылка
Юнусов А.А., Дасибеков А. ОДНОРАЗМЕРНАЯ ЗАДАЧА КОНСОЛИДАЦИИ НАСЛЕДСТВЕННО – СТАРЕЮЩИХ ТРЕХФАЗНЫХ ГРУНТОВ // Международный журнал экспериментального образования. – 2015. – № 7. – С. 70-74;URL: https://expeducation.ru/ru/article/view?id=7730 (дата обращения: 21.11.2024).