Успех исследовательской деятельности учащихся в основном обеспечивается правильным планированием видов и форм заданий, использованием эффективных систем заданий, а также умелым руководством учителя этой деятельностью.
Раскрывая роль учителя в организации учебного исследования, отметим следующую систему его действий: умение выбрать нужный уровень проведения учебного исследования в зависимости от уровня развития мышления учащегося; умение сочетать индивидуальные и коллективные формы проведения исследований на уроке; умение формировать проблемные ситуации в зависимости от уровня учебного исследования, его места в структуре урока и от цели урока.
Учитель должен выступать не столько в роли интерпретатора науки и носителя новой информации, сколько умелым организатором систематической самостоятельной поисковой деятельности учащихся по получению знаний, приобретению умений и навыков и усвоению способов умственной деятельности.
В процессе исследовательской деятельности учащиеся овладевают некоторыми навыками наблюдения, экспериментирования, сопоставления и обобщения фактов, делают определенные выводы. Необходимо создавать условия, способствующие возникновению у учащихся познавательной потребности в приобретении знаний, в овладении способами их использования и влияющие на формирование умений и навыков творческой деятельности.
Развивающая функция исследовательской деятельности по математике заключается в том, что в процессе ее выполнения происходит усвоение методов и стиля мышления, свойственных математике, воспитание осознанного отношения к своему опыту, формирование черт творческой деятельности и познавательного интереса к различным аспектам математики.
Особую роль в интеллектуальном развитии учащихся играет исследовательская деятельность учащихся, непосредственно связанная с усвоением математических знаний. Поэтому успешное решение стоящих перед школой задач возможно посредством приобщения учащихся к исследовательской деятельности и развития способностей к ней в процессе обучения.
Основным признаками учебного исследования являются:
а) постановка познавательной проблемы и цели исследования;
б) самостоятельное выполнение обучающимися поисковой работы;
в) направленность учебного исследования обучающихся на получение новых для себя знаний;
г) направленность учебного исследования на реализацию дидактических, развивающих и воспитательных целей обучения.
Поисково-исследовательская деятельность – это процесс решения поставленной проблемы на основе самостоятельного поиска теоретических знаний; предвиденье и прогнозирование как результатов решения, так и способов и процессов деятельности.
К факторам, способствующим формированию учебно-исследовательской деятельности учащихся, можно отнести следующие: личностно ориентированный подход к обучению; ориентация на продуктивное достижение результата; проблемное обучение как инструмент развития опыта творческой деятельности; оптимальное сочетание логических и эвристических методов решения задач; креативная организация учебного процесса, максимальное насыщение его творческими ситуациями; создание ситуации совместной поисковой деятельности; детализация учебного процесса; создание психологической атмосферы, оптимальных условий для творческой деятельности.
Условиями, способствующими активизации поисково-исследовательской деятельности учащихся, являются: доброжелательная атмосфера в коллективе; сочетание индивидуальных и коллективных форм обучения; структурирование учебного материала по принципу нарастания познавательной трудности учебной работы; вооружение учащихся рациональными приемами познавательной деятельности; формирование внутренних стимулов к учению, самообразованию и др.
На основе обобщения и анализа результатов теоретических исследований по данной проблеме нами были выделены следующие основные признаки учебных исследований: процесс поисковой познавательной деятельности; потребность получения чего-либо нового; самостоятельный поиск; направленность на достижение целей обучения; формирование специальных эвристик.
Итак, под учебным исследованием мы будем понимать такой вид познавательной деятельности учащихся, который способствует формированию следующих умений: добывать новые предметные знания, приемы и способы действий; самостоятельно организовывать поиск; достигать поставленных целей обучения; формировать мыслительные операции, такие как аналогия, классификация, обобщение и т.п.
При более детальном анализе структуры учебного исследования можно выделить и такие его этапы, как: мотивация учебной деятельности; постановка проблемы исследования; анализ имеющейся информации по рассматриваемому вопросу; экспериментирование (проведение измерений, испытаний, проб и т.д.) с целью получения фактического материала; систематизация и анализ полученного фактического материала; выдвижение гипотезы; подтверждение или опровержение гипотез; доказательство гипотез.
Приведем примеры исследовательских заданий по математике, которые учащиеся могут выполнить с использованием информационно-коммуникационных технологий.
1. Прямые, содержащие высоты треугольника, вписанного в гиперболу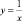 
, пересекаются в точке, лежащей на гиперболе.
Естественно, напрашивается некоторое обобщение этого факта. Учащимся, например, можно предложить провести исследование такого вопроса: «Обладают ли такими свойствами кривые, задаваемые уравнениями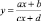 
?».
Далее целесообразно рассмотреть такой вопрос: «Не будут ли прямые, содержащие высоты треугольника, вписанного в график функции у = ax, пересекаться в точке, лежащей на графике обратной функции y = logax?».
Заметим, что исследование поставленных вопросов можно провести с помощью как чисто математических выкладок, так и компьютерного эксперимента.
Ниже мы приведем задачи, связанные с понятием палиндрома (русский эквивалент – «перевертыш») – это слово, фраза или выражение, одинаково читающееся с начала и с конца (без учета пропусков между словами и знаков препинания). Например, слово «шалаш». В математике под палиндромом чаще всего понимают число, имеющее одинаковые значения при чтении слева направо и наоборот. Например, 515. Среди таких «перевертышей» почему-то популярны полные квадраты.
2. Найдите шестизначное число, являющееся палиндромом и точным квадратом. Ответ 698896 = 8362, возможно, не единственный.
Решение на языке программирования JSCRIPT
Метод состоит в том, чтобы перебрать все шестизначные числа, определить какие из них палиндромы и точные квадраты (метод перебирает 900000 чисел):
Еще одно решение на языке программирования JSCRIPT
Метод генерирует шестизначные числа, являющиеся палиндромами, и определяет будут ли они точными квадратами (метод перебирает 1000 чисел):
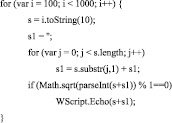
Оба метода доказывают, что число 698896 = 8362 – единственное решение задачи.
3. Опишите множества двузначных, трехзначных и четырехзначных палиндромов – точных квадратов. Приведите пример палиндрома такого вида пятизначного.
Решение
Искомых двузначных палиндромов, очевидно, нет: числа 11, 22,…, 99 не являются квадратами.
Пусть имеем палиндром
A = aba = 100a + 10b + a.
Если он является квадратом, то последняя (как и первая цифра) – это 1 или 4 или 5 или 6 или 9. Перебором находим нужные числа:
121 = 112; 484 = 222; 676 = 262.
Рассмотрим четырехзначный палиндром
A = abba = 103a + 102b + 10b + a.
Представим его в виде
A = 1001a + 110b = 11∙(91a + 10b).
Чтобы это число было полным квадратом, необходимо и достаточно, чтобы выражение в скобках имело вид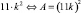 
. Здесь k ∈ [3, 9] (иначе (11k)2 не четырехзначное). Но квадраты чисел 33, 44, …, 99 не являются «перевертышами». Следовательно, множество квадратных четырехзначных палиндромов пусто.
Легко построить пятизначный палиндром – квадрат, если подметить, что
121 = 112; 12321 = 1112; 1234321 = 11112, ...
121 = 112; 10201 = 1012; 1002001 = 10012, ...
484 = 222; 40804 = 2022; 4008004 = 20022, ...
44944 = 2122; 404090404 = 201022;
4004009004004 = 20010022, ...
Это наблюдение позволяет строить нужный палиндром нечетной значности:
7 – значный, 9 – значный, … вплоть до 19 – значного.
Решение на языке программирования JSCRIPT
Метод генерирует семизначные числа, являющиеся палиндромами и определяет являются ли они точными квадратами.
Разнообразные задачи на использование метода перебора читатель найдет в наших работах [1; 2; 3; 4; 5].
Библиографическая ссылка
Далингер В.А. ИНФОРМАЦИОННО-КОММУНИКАЦИОННЫЕ ТЕХНОЛОГИИ В ОРГАНИЗАЦИИ УЧЕБНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ УЧАЩИХСЯ ПО МАТЕМАТИКЕ // Международный журнал экспериментального образования. – 2015. – № 11-3. – С. 419-422;URL: https://expeducation.ru/ru/article/view?id=8443 (дата обращения: 21.11.2024).