Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Файлы
• Литература

Должиков В.Н. 1 Должикова Е.Н. 1

---

1 ФГБОУ ВПО «Сочинский государственный университет»

Статья в формате PDF

356 KB

1. Райзер В.Д., Должиков В.Н., Должикова Е.Н. Определение оптимальных параметров составных пластин методом нелинейного программирования // Строительная механика и расчет сооружений. – 1987. – № 1. – С. 21–23.

2. Должикова Е.Н. Оптимизация параметров ортотропных составных пластин: дис. … канд. техн. наук. – М.: МИСИ,1986. – 162 с.

3. Хилл Р. Математическая теория пластичности. – М.: Гостехиздат, 1956. – 407 с.

4. Ермолов С.Б. Устойчивость пластинок на упругом основании и элементов гофрированных обшивок трехслойных панелей // Расчет конструкций с применением пластмасс: Тр. ЦНИИСК им. В.А. Кучеренко. – 1974. – С. 101–108.

Широкое применение металлических трехслойных панелей в строительстве обуславливает актуальность исследовательских работ, направленных на совершенствование конструктивных решений при одновременном снижении расхода материалов и стоимости конструкций. Известно, что трехслойные конструкции с металлическими гофрированными обшивками в 15–20 раз легче традиционных железобетонных и легкобетонных конструкций.

Учитывая то, что затраты на материалы, применяемые для составных пластилин, составляют 90–92 % [1] от общей стоимости, в качестве целевой функции принимается стоимость материала конструкции С, которая имеет следующий вид:

С = V₁P₁ + V₂P₂, (1)

где V₁, V₂ – соответственно объём материала обшивок и заполнителя; P₁, P₂ – стоимость единицы объема материалов обшивки и заполнителя.

Принимая конструкцию обшивки с трапецеидальными гофрами, функция цели записывается в следующем виде:

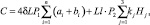(2)

где δ – толщина обшивки листа; n – количество гофров на ширину пластины В; L – длина пластины; l – длина участков поперечного сечения пластины с одинаковыми параметрами гофров; a_i – ширина полки i-го гофра; k_i – количество гофров на j-м участке поперечного сечения пластины; H_j – расстояние между геометрическими слоями обшивок; H₀ – толщина слоя заполнителя, подкрепляющего внутренние полки профиля обшивок; b_i – длина наклонной стенки i-го трапецеидального гофра.

Для решения математической модели трехслойной пластины с гофрированными обшивками использован подход к проектированию дискретно – равнопрочных составных изгибаемых пластин, основанный на принципе дискретной равнопрочности [2].

При дискретизации конструкции аналитические функции физических величин заменяются конечными множествами значений этих величин в фиксированных областях. Такие множества удобно считать векторными в многомерном пространстве. Срединная плоскость рассматриваемой пластины покрывалась расчетной сеткой, узловые точки которой приобретают смысл расчетных сечений.

Уравнения равновесия действительны для всех внутренних точек и являются ограничением в виде равенств для целевой функции. В качестве ограничений типа неравенств в настоящей задаче использованы нелинейные условия прочности Хилла [3], которые являются условием прочности для внешних слоев пластины. Для заполнителя использованы ограничения типа:

|τ_max| ≤ R_T2,

где R_T2 – расчетное сопротивление материала заполнителя сдвигу.

Расчет гофрированных конструкций сопряжен со значительными трудностями, которые возникают из-за сложной метрики их срединной поверхности. Поэтому при оптимизации трехслойной пластины расчет упрощался путем замены гофрированного элемента пластины эквивалентным ему гладким. Нахождение параметров эквивалентного элемента пластины выполнялось посредством приравнивания изгибных жесткостей гофрированного и эквивалентного ему элемента

EI = EI^экв.

Для сжатых полок трапецеидального гофра обшивок пластины вводились ограничения по местной устойчивости σ ≤ σ_кр. Полки гофров рассматривались как удлиненные, шарнирно опертые, прямоугольные пластины на упругом основании, которым служит средний слой пластины, имеющий коэффициент постели [4]

k = E₃/H_п,

где E₃ – модуль упругости заполнителя; H_п – толщина подкрепляющего слоя.

При расчете на местную устойчивость полок трапецеидальных гофрированных обшивок критическая сила определялась по формуле [4]

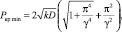(3)

где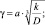

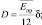
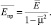
Здесь 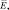– модуль упругости и коэффициент Пуассона материала обшивки; D – цилиндрическая жесткость пластины. Подставляя в (3) выражения для входящих параметров и учитывая, что σ_кр = P_кр/δ после преобразования получили выражение критических напряжений:

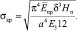
Кроме выше перечисленных ограничений условия технологической осуществимости и теплотехнического расчета требовали выполнения ограничения по минимальной толщине среднего слоя. Выборочные результаты расчетов приведены в таблице.

Библиографическая ссылка