Проективная геометрия развилась и выделилась в особую ветвь геометрических знаний в первые десятилетия 19 века. Источником этого явились потребности графики и архитектуры, развитие теории изображений в перспективе. Французский геометр Понселе одним из первых выделил особые свойства геометрических фигур, названные им проективными. Понселе назвал предмет, изучающий проективные свойства – проективной геометрией. Плоскость, дополненная бесконечно удалённой прямой названа проективной плоскостью. Пространство, дополненное бесконечно удалённой плоскостью названо проективным пространством. Взгляд Лобачевского на создание неевклидовой геометрии.
Проективная геометрия – раздел геометрии, изучающий свойства фигур, не меняющихся при проективных преобразованиях, например, при проектировании. Такие свойства называются проективными, к ним относятся, например, прямолинейное расположение точек, порядок алгебраической кривой и т.д.
Проективная геометрия развилась и выделилась в особую ветвь геометрических знаний в первые десятилетия 19 века. Источником этого явились потребности графики и архитектуры, развитие теории изображений в перспективе.
Французский геометр Ж. Понселе одним из первых выделил особые свойства геометрических фигур, названные им проективными.
О свойствах геометрических фигур
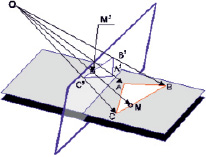
Пусть K – произвольная фигура в некоторой плоскости П, П’ – какая-либо другая плоскость, точка О – произвольная точка пространства, не принадлежащая ни одной плоскости (П и П’). Точка О, соединенная с любой точкой М фигуры K (рисунок), определяет прямую (ОМ), пересекающую плоскость П’ в некоторой точке М’, которую мы будем называть проекцией точки М (на плоскости П’ из центра О).
Проекции всех точек фигуры K на плоскость П’ составят некоторую фигуру K’, которая называется проекцией фигуры K. Операция, с помощью которой в данной задаче из фигуры K получена фигура K’ носит название центрального проектирования из точки О. Если изменить положение точки О и плоскости П’ мы получим бесконечное множество фигур (или иначе говоря, центральных проекций фигуры K), которые в чем-то будут похожи на фигуру K, но в чем-то и отличаться. Например, проектируя правильный треугольник, получим тоже треугольник, но произвольной формы. Проектируя окружность, можем получить эллипс или параболу, или даже гиперболу. При таком проектировании не сохраняются метрические характеристики фигур (длина, площадь и т.д.).
Выясним, какие же свойства сохраняются. Они обычно называются инвариантами преобразования, каковым в данном случае является преобразование проектирования. Именно эти свойства фигур, инвариантные по отношению к такому проектированию, Понселе назвал проективными свойствами, а предмет, их изучающий – проективной геометрией.
При проектировании точек одной плоскости П на другую плоскость П’ не каждая точка П’ имеет прообраз в П и не каждая точка из П имеет образ в П’. Это обстоятельство привело к необходимости дополнения евклидова пространства, так например, бесконечно удалёнными элементами (несобственными точками, прямыми и плоскостью) и к образованию нового геометрического объекта – трёхмерного проективного пространства. При этом каждая прямая дополняется одной несобственной точкой, каждая плоскость – несобственной прямой, всё пространство – одной несобственной плоскостью.
Параллельные прямые дополняются одной и той же несобственной точкой, непараллельные – разными, параллельные плоскости дополняются одной и той же несобственной прямой, непараллельные – разными. Несобственные точки, которыми дополняется плоскость, принадлежат несобственной прямой, дополняющей ту же плоскость. Все несобственные точки и несобственные прямые принадлежат несобственной плоскости. Дополнение евклидова пространства до проективного пространства приводит к тому, что проектирование становиться взаимно однозначным. Аналогичная процедура применима и для n – мерного пространства.
Существуют различные способы аксиоматического построения проективного пространства. Наиболее распространенным является видоизменение системы аксиом, предложенной в 1899 году Д. Гильбертом (D. Hilbert) для обоснования элементарной геометрии. Все остальные понятия Евклидовой геометрии определяются с помощью основных понятий Гильберта системы аксиом, а все предложения о свойствах геометрических фигур, не содержащиеся в Гильберта системе аксиом, должны быть доказаны чисто логическим выводом из этих аксиом (или предложений, полученных таким же путём). Гильберта система аксиом обладает свойством полноты; она непротиворечива, если непротиворечива арифметика действительных чисел. Если в Гильберта системе аксиом заменить аксиому о параллельных её отрицанием, то полученная новая система аксиом тоже непротиворечива (система аксиом геометрии Лобачевского), т.е. аксиома о параллельных не зависит от остальных аксиом Гильберта системы аксиом. Можно установить независимость некоторых других аксиом Гильберта системы аксиом от остальных аксиом этой системы. Гильберта система аксиом является первым достаточно строгим обоснованием евклидовой геометрии [1, 5].
Проективное пространство рассматривается как совокупность элементов трёх рядов: точек, прямых и плоскостей, между которыми установлено основное для проективной геометрии отношение инцидентности, характеризующееся надлежащими аксиомами. Они отличаются от соответствующей группы аксиом элементарной геометрии тем, что требуют, чтобы каждые две прямые, лежащие в одной плоскости, имели общую точку, и на каждой прямой имелось, по крайней мере, три различные точки. В конкретных случаях для получения более «богатой» проективной геометрии, эта совокупность аксиом дополняется аксиомами порядка и непрерывности (для действительного проективного пространства), Паппа аксиомой (для проективной геометрии над коммутативным телом), Фано постулатом (для проективной геометрии над телом, характеристика которого ≠ 2) и т.д.
Замечательным положением в проективной геометрии является двойственности принцип. Говорят, что точка и прямая (точка и плоскость, прямая и плоскость) инцидентны, если точка лежит на прямой (или прямая проходит через точку) и т.д. Тогда если верно некоторое предложение А о точках, прямых и плоскостях проективного пространства, сформулированное только в терминах инцидентности между ними, то будет верно и двойственное положение В, которое получается на А заменой слова «точка» на слово «плоскость», на слово «точка» и с сохранением слова «прямая».
Важную роль в проективной геометрии играет Дезарга предложение, выполнение которого необходимо и достаточно для введения проективными средствами системы проективных координат, составленных из элементов некоторого тела К, естественным образом связанного с точками проективной прямой. Дезарг Жерар (G. Desargues) французский математик, архитектор и инженер. Заложил в 17в. основы начертательной и проективной геометрии [2,3].
О инвариантных свойствах
Большое значение для последующего развития проективной геометрии имели работы Б. Паскаля (B. Pascal) (в связи с изучением им некоторых свойств конических сечений) и Г. Монжа (G. Monge, 2-я пол. 18 – нач. 19 вв.). Как самостоятельная дисциплина проективная геометрия была изложена Ж. Понселе (J. Poncelet нач. 19 в.). Заслуга Ж. Понселе заключалась в выделении проективных свойств фигур в отдельный класс и установлении соответствий между метрическими и проективными свойствами этих фигур. К этому же периоду относятся работы Ж. Брианшона (J. Brianchon). Дальнейшее развитие проективная геометрия получила в трудах Я. Штейнера (J. Steiner) и М. Шаля (M. Chasles). Большую роль в развитии проективной геометрии сыграли работы К. Штаудта (Ch. Staudt), в которых были намечены также контуры аксиоматического построения проективной геометрии. Все эти геометры стремились доказывать теоремы проективной геометрии синтетическим методом, положив в основу изложения проективные свойства фигур. Аналитическое направление в проективной геометрии было намечено работами А. Мёбиуса (A. Möbius). Влияние на развитие проективной геометрии оказали работы Н.И. Лобачевского по созданию неевклидовой геометрии. Достоверно то, что уже в начале 1819 г. у Лобачевского была рукопись составленного им сочинения, которое содержало изложение основных начал геометрии. Сочинение, представленное им к напечатанию в 1823 г. носило название «Геометрия» и построение его очень существенно отличалось от обычной структуры курса элементарной геометрии Евклида, то есть перестраивало систему геометрии, подойдя критически к традиционной системе Евклида [4].
Заключение. Неевклидовая геометрия стала наиболее впечатляющим, интеллектуальным свершением 19в. Она ясно продемонстрировала, что математику нельзя более рассматривать как свод непререкаемых истин. В лучшем случае математика может гарантировать достоверность доказательства на основе недостоверных аксиом. Но зато математики впредь обрели свободу исследовать любые идеи, которые могли показаться им привлекательными и позволившие в дальнейшем А. Кэли (A. Cayley) и Ф. Клейну (F. Klein) рассмотреть различные геометрические системы с точки зрения проективной геометрии. Развитие аналитических методов обычной проективной геометрии и построение на этой базе комплексной проективной геометрии (Э. Штуди, E. Study, Э. Катан, E. Cartan) поставили задачу о зависимости тех или иных проективных свойств от того тела, над которым построена геометрия. В решении этого вопроса больших успехов добились А.Н. Колмогоров и Л.С. Понтрягин.
Библиографическая ссылка
Галагузова Т.А., Маначинская А.В., Галагузова Г.Ф. О ПРОЕКТИВНОЙ ГЕОМЕТРИИ И ЕЁ СВОЙСТВАХ // Международный журнал экспериментального образования. 2015. № 11-5. С. 636-638;URL: https://expeducation.ru/ru/article/view?id=8780 (дата обращения: 07.01.2026).

