Современное профессиональное образование в Республике Казахстан ориентировано на переход от «знаниевой» к личностно-ориентированной парадигме обучения. Исходя из этого, проведение в начальном звене школы регулярных развивающих занятий, включение учащихся в постоянную поисковую деятельность существенно гуманизирует учебный процесс. Такой подход создает условия для развития у учащихся познавательных интересов, стимулирует стремление ученика к размышлению и поиску, вызывает у него чувство уверенности в своих силах, в возможностях своего интеллекта. Во время таких занятий у учеников происходит становление и развитие форм самосознания и самоконтроля, исчезает боязнь ошибочных шагов, снижается тревожность и необоснованное беспокойство, тем самым создаются необходимые личностные и интеллектуальные предпосылки для успешного протекания процессов обучения на следующих этапах [1].
Предполагаемое интеллектуальное развитие личности школьника, важнейшим компонентом которой является формирование логических умений, операций и приемов их составляющих, обусловлена рядом следующих обстоятельств: качество усвоения знаний во многом зависит от уровня развития мышления; организация умственного труда основывается на выборе и последовательном осуществлении оптимальных для данной ситуации форм, методов и приемов деятельности; в информатизации образования; в единстве и взаимосвязи с развитием мышления идет развитие речи; в умении организовать свою умственную деятельность [2].
Никто сегодня, как показывает изучение, не будет спорить с тем, что каждый учитель должен развивать интеллектуальное мышление учащихся. Об этом говорится в методической литературе, в объяснительных записках к учебным программам. Однако, как это делать, учитель не всегда знает. Нередко это приводит к тому, что развитие интеллекта и мышления в значительной мере идет стихийно, поэтому большинство учащихся, даже старшеклассников, не овладевает начальными приемами логического мышления (анализ, синтез, сравнение, абстрагирование и др.).
Цель исследования: определить наиболее эффективные и содержательные компоненты методической системы по интеллектуальному развитию школьников.
Объект исследования: процесс обучения математике в основной школе.
Методы исследования:
– изучение и анализ психолого-педагогической и методической литературы, относящейся к исследуемой проблеме;
– наблюдение за педагогическим процессом в основной школе;
– изучение и обобщение передового педагогического опыта педагогов.
Задачи исследования:
1. Проанализировать особенности интеллектуального развития школьников в процессе обучения в основной школе.
2. Выделить пути интеллектуального развития школьников.
3. Выявить содержательные компоненты методической системы по интеллектуальному развитию школьников в процессе обучения и воспитания.
Результаты исследования: Рассмотрим состояние педагогической проблемы интеллектуального развития учащихся в процессе обучения математике в основной школе.
Для этого мы проанализировали психолого-педагогическую литературу, журнальные статьи («Начальная школа», «Школа», «Творческая педагогика» и т.д.), а также материалы из газет («Учитель Казахстана», приложения к газете «1 сентября» и т.д.).
Как показал проводимый анализ литературы, мы выявили ряд авторов занимающихся проблемой интеллектуального развития школьников и их позициями по интересующим нас вопросам. Это: Н.С. Антонов, В.А. Гусев, Н.Б. Бабкин, О.Б. Богомолова, Е.А. Ведемина, Г.Д. Глейзер, Е.Ж. Жунусов, Т.Г. Зайцев, А.З. Зак и другие.
Рассмотрев научные позиции некоторых авторов мы пришли к следующему определению собственной точки зрения. Анализ литературы показал, что понятие «интеллект» тесно связано с развитием умственных способностей индивида, с его способностью мышления.
Интеллект – система психологических механизмов, обусловливающих возможность строить внутри индивида адекватную модель (картину) окружающего мира и оптимально организовывать свое поведение и деятельность в нем, создавая порядок из хаоса на основе приведения в соответствие индивидуальных потребностей с объективными требованиями реальности. Таково самое общее определение понятия интеллекта, которое разными авторами трактуется по-разному. Обратимся к западноевропейской тестологии, которой в течение столетия принадлежала монополия в изучении интеллекта. Прежде всего приведем определение В. Штерна: «Интеллект – это общая способность индивидуума осознанно настраивать свое мышление на возникшие требования. Это общая умственная приспособляемость к новым задачам и условиям действительности». Д. Векслер определяет интеллект как комбинированную и глобальную способность индивида к адекватным поступкам, здравому мышлению и эффективному взаимодействию с окружающей действительностью. По мнению Р. Зиглера и Д. Ричардса, «интеллект – это понятие, которое нельзя определить через какие-либо отличительные особенности, но только через определенное количество поведенческих «прототипов». Дж. Томпсон считает, что «интеллект – это не прямо идентифицируемое психическое качество, а всего лишь абстрактное понятие, которое упрощает и суммирует определенные поведенческие проявления». П. Гилфорд рассматривает интеллект как способность обрабатывать информацию, причем под информацией он понимает весь спектр восприятия человека. Согласно Борингу, в действительности интеллект – это то, что измеряют интеллектуальные тесты.
Дженсен, Айзенк, Херристайн и др. рассматривают «операциональное» определение интеллекта не как ступень в развитии теории, а как достаточное основание для построения теории. Понятие становится основой для измерения реальности, поскольку утверждается, что интеллект определяется методом его измерения. Такой подход к интеллекту явно смыкается с философским идеализмом. Он преднамеренно приводит к тому, что вне процесса тестирования термин «интеллект» теряет всякий смысл, т.к. он противопоставляется естественным проявлениям интеллектуальной активности, творческим интеллектуальным возможностям (креативности), эффективности социального познания (социальной компетентности).
Оценивая итоги аналитической работы по определению интеллекта, мы не можем обойти стороной термин «интеллектуальная активность».
Интеллектуальная активность – не стимулированное извне продолжение мышления [3]. Применив терминологию системного подхода к исследованию психологических процессов и явлений, можно определить интеллектуальную активность как интегральное свойство некоторой гипотетической системы, основными компонентами (или подсистемами) которой являются интеллектуальные (общие умственные способности) и неинтеллектуальные (прежде всего – мотивационные) факторы умственной деятельности. При этом интеллектуальная активность не сводится ни к тем, ни к другим в отдельности. Умственные способности составляют как бы фундамент интеллектуальной активности, определяя широту и глубину познавательного интереса, но проявляются в ней не непосредственно, а лишь преломляясь через структуру личности.
В настоящее время наряду с исторически первым рабочим понятием «интеллектуальная активность» в работах Д.Б. Богоявленской используются также понятия: «духовная активность», «ситуативно не стимулированная продуктивная деятельность», «продолжение мышления за пределами ситуативной заданности», «познавательная самодеятельность», которые понимаются автором как синонимы, но каждое из них несет свою «нагрузку», оттеняет одну из сторон изучаемого феномена.
Мерой интеллектуальной активности, ее наиболее интимной качественной характеристикой может служить интеллектуальная инициатива. Последнюю следует понимать как продолжение мыслительной деятельности за пределами ситуативной заданности, не обусловленной ни практическими нуждами, ни внешней или субъективной отрицательной оценкой работы. При этом интеллектуальную инициативу не следует отождествлять с проявлением любой инициативы в интеллектуальной сфере. Ее следует отличать, во-первых, от инициативы выбора, предпочтения мыслительной работы другим видам работы, во-вторых, от стремления к перевыполнению задания, когда сверх заданного в эксперименте (в жизненных ситуациях также) испытуемый просит дать ему еще одну, две и т.д. задачи. Последнее может быть проявлением не интеллектуальной инициативы, а самоутверждения на фоне эмоционального подкрепления.
Д.Б. Богоявленская рассматривает интеллектуальную активность в качестве единицы анализа творчества.
Интеллектуальное развитие – формирование способности к овладению и пользованию различными типами мышления (эмпирическим, образным, теоретическим. конкретно-историческим, диалектическим и т.д. в их единстве). Его органической частью является умение подвергать самостоятельному анализу события и явления действительности, делать самостоятельные выводы и обобщения, а также речевое развитие: владение и свободное пользование словарным богатством языка. Содержательной стороной интеллектуального развития является общедуховное, включающее в себя определенный объем основных научных знаний о мире и способность философской, конкретно-исторической оценки действительности.
Роль математики в развитии математического мышления исключительно велика.
Причина столь исключительной роли математики в том, что это самая теоретическая наука из всех изучаемых в школе. В ней высокий уровень абстракции и в ней наиболее естественным способом изложения знаний является способ восхождения от абстрактного к конкретному.
Существует общее мнение об активной работе в процессе математического мышления определенных качеств мышления (например, гибкость, пространственное воображение, умение выделять существенное и т.д.), которые в равной степени могут быть соотнесены как к математическому мышлению, так и к мышлению физическому, техническому и т.д., т.е. к научному мышлению вообще.
Эти особенности мышления мы будем называть качествами научного мышления. Они представляют особую дидактическую значимость: формирование их у школьников способствует не только успешному обучению математике, но и успешному обучению другим предметам естественно-математического цикла.
Вопросы методики изучения математических предложений, понятий рассматривались в работах казахстанских методистов Абылкасымовой А.Е. [4], Жуматаева Е. [5].
На наш взгляд, целенаправленность мышления характеризуется стремлением осуществлять разумный выбор действий при решении какой-либо проблемы, постоянно ориентируясь на поставленную той проблемой цель, а также в стремлении отыскать наиболее кратчайшие пути ее достижения.
Наличие у школьников этого качества мышления особенно важно при поиске плана решения математических задач, при изучении нового материала и т.д.
Этому способствуют специально подобранные учителем задачи, вводящие в изучение новой темы, посредством которых перед учащимися раскрывается целесообразность ее изучения и последовательность рассмотрения относящихся к ней вопросов.
Целенаправленность мышления дает возможность более экономичного решения многих задач, которые обычным способом решается если не сложно, то слишком долго.
Целенаправленность мышления тесно связана с таким нравственным качеством личности, как любознательность, своеобразным антиподом которому является любопытство. В основе того и другого качества личности лежат условные рефлексы, в силу которых избирательная активность человека всегда имеет целенаправленный, намеренный характер.
Первое из этих качеств (любознательность) обогащает знания и опыт человека именно в силу своей целенаправленности; любопытство, превращаясь в самоцель, гасит стремление человека к познанию, как только оно удовлетворено. Поэтому в обучении математике следует всячески поощрять любознательность учащихся.
Рациональность мышления часто проявляется при наличии широты мышления, которая характеризуется способностью к формированию обобщенных способов действий, имеющих широкий диапазон переноса и применения к частным, нетипичным случаям; умение охватить проблему в целом, не упуская при этом имеющих значение деталей; обобщить проблему, расширить область приложения результатов, полученных в процессе ее разрешения. Поэтому широту мышления часто называют обобщенностью мышления.
Это качество мышления проявляется в готовности школьников принять во внимание новые для них факты в процессе деятельности в известной (знакомой им) ситуации.
Широта мышления учащихся проявляется также в умение классифицировать и систематизировать изучаемые математические факты, обобщать их, использовать обобщение и аналогию как методы решения задач.
Все рассмотренные выше качества мышления могут проявиться лишь при условии проявления активности мышления, которая характеризуется постоянством усилий, направленных на решение некоторой проблемы, желанием обязательно решить поставленную проблему, изучить различные подходы к ее решению, исследовать различные варианты постановки этой проблемы в зависимости от изменяющихся условий и т.д.
Как показывает опыт, одним их эффективных способов развития мышления являются и разные способы решения геометрических задач.
В геометрии известны задачи и теоремы, которые допускают несколько способов решения, что, безусловно, активизирует познавательную деятельность учащихся, способствует их интеллектуальному и творческому развитию. Решая задачу несколькими непохожими друг на друга способами, учащиеся привлекают разнообразный теоретический материал из всего курса. Одной из таких наиболее известных теорем является теорема Пифагора, доказываемая большим количеством способов, а также задачи о свойствах биссектрисы угла делить противоположную сторону на части, пропорциональные прилежащим, и задача о свойствах медиан треугольника, делящих его на шесть равновеликих треугольников.
Рассмотрим один из способов решения задачи о свойствах медиан треугольника. Как известно, в планиметрии есть замечательная теорема, которая незаслуженно обделена вниманием авторов традиционных школьных учебников по геометрии, так как допускает несколько различных вариантов решения с привлечением большого количества теоретических вопросов. Это теорема о свойствах медиан треугольника:
Медианы треугольника делят его на шесть равновеликих треугольников.
Чтобы доказать эту теорему, предварительно докажем утверждение задачи: «Медиана треугольника делит его на два равновеликих треугольника».
Дано: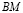 
– медиана.
Доказать: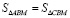 
.
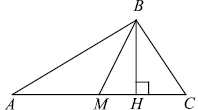
Доказательство. Проведем высоту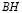 
данного треугольника 
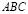, которая является также высотой треугольников 
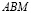и 
. И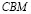меем
, 
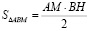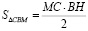
Так как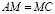 
по условию и 
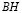– общая высота, то 
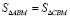, т.е. треугольник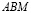и 
и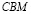 
равновелики.
Далее рассмотрим один из способов доказательства теоремы о свойствах медиан треугольника. Для этого воспользуемся следующими свойствами:
1) свойством площадей треугольников, имеющих равные углы: площади треугольников, имеющих равные углы, относятся как произведение сторон, заключающих равные углы;
2) свойством медиан: медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
Доказательство. Треугольник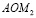и 
и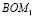 
имеют равные углы: 
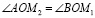(как вертикальные). Далее имеем:
.
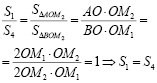Аналогично доказывается, что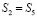 
, 
, 
, 
, 
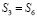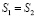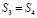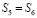(это следует из предварительной задачи). Следовательно, 
.
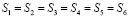Как показывает изучение, решение задач такого типа в учебном процессе школы способствует мотивации ее введения, помогают выявлять учащимся закономерности, отраженные в теореме; способствуют усвоению ими содержания теоремы; обеспечивают восприятие идеи доказательства, раскрывают приемы доказательства; обучают применению теоремы; раскрывают взаимосвязи изучаемой теоремы с другими теоремами.
Выводы. Нужно отметить, что интеллектуальное развитие школьников обеспечивается разнообразием организационных форм и учетом индивидуальных особенностей каждого обучающегося, ростом творческого потенциала, познавательных мотивов, обогащением форм взаимодействия со сверстниками и взрослыми в познавательной деятельности.
Библиографическая ссылка
Кошкимбаева Р.Х., Сыдыхов Б.Д., Керимбеков М.А., Жунисбекова Ж.А. ИНТЕЛЛЕКТУАЛЬНОЕ РАЗВИТИЕ ШКОЛЬНИКОВ В ПРОЦЕССЕ ИЗУЧЕНИЯ МАТЕМАТИКИ // Международный журнал экспериментального образования. – 2015. – № 12-2. – С. 195-199;URL: https://expeducation.ru/ru/article/view?id=9040 (дата обращения: 21.11.2024).