Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Файлы
• Литература

Щипицын А.Г. 1

---

1

Статья в формате PDF

2346 KB

1. Казаков И.Е. Статистическая теория систем управления. – М.: Наука, 1975. – 432 с.

2. Квакернаак Х, Сиван Р. Линейные оптимальные системы управления. – М.: Мир, 1977. – 653 с.

3. Синицын И.Н. Фильтры Калмана и Пугачёва. – М.: Логос, 2006. – 640 с.

4. Щипицын А.Г. Программное обеспечение оценивания состояния динамического процесса с эффективными ограничениями на его параметры // Свидетельство о регистрации электронного ресурса № 21249 от 15.10.2015. – 31 с.

Постановка задачи. Рассматривается процесс с математическим описанием априорной переменной состояния (АПС)

dY /dt = aY+u+gK, Y (t0)=Y 0, t0 ≤t≤T, (1)

где Y – АПС процесса, a – основной параметр процесса (ОПР), u – управляющее воздействие (УВ), K – безразмерная центрированная случайная величина (ЦСВ), g – масштабный множитель при ЦСВ K, [t 0, T] – интервал времени наблюдения процесса (ИВНП), Y0 – значение АПС при t=t0; параметры a, u, g, t0, T – детерминированные положительные постоянные. Применяя операцию математического ожидания (МО) к уравнению (1), получаем уравнение относительно эталонной переменной состояния (ЭПС) процесса

dy /dt = ay+u, y (t 0)=y0, t0 ≤t≤T, (2)

где y0 – значение ЭПС при t=t0.

Наблюдение за процессом осуществляется измеряемой переменной состояния (ИПС), называемой также измерителем

Z = cy+hL, (3)

где c – масштабный коэффициент; L – безразмерная ЦСВ; h – масштабный множитель при ЦСВ L; параметры c; h – детерминированные положительные постоянные.

Общая задача заключается в построении оптимального фильтра вида

dX /dt = aX+p (Z –cX)+u,

X (t0)=X 0, t0 ≤t≤T, (4)

где X – фильтрованная переменная состояния (ФПС) процесса; p – основной параметр фильтра, определяемый с использованием уравнения Риккати [1]

dR /dt = 2aR–qR 2+M,

R (t0)= Y 0 , t0 ≤t≤T, (5)

по формуле

p = cR /N, (6)

и в (5) обозначено

q = c 2 /N. (7)

В уравнении (5) и в выражениях (6), (7) введены обозначения: M, N – характеристики соответственно априорной и измерительной погрешностей, которые в теории линейной оптимальной фильтрации [1] представляют собой интенсивности априорного и измерительного шумов; Y 0 – дисперсия начального условия для АПС Y0.

В поставленной общей задаче с измерителем вида (3), у которого погрешность представляет собой произведение детерминированного параметра h на ЦСВ L, предлагается использовать уравнение (5) для определения параметра (6), а указанные выше характеристики M, N поставить в соответствие случайным погрешностям gK, hL реализацией следующей процедуры.

Если математическое описание динамического процесса представлено линейным дифференциальным уравнением первого порядка

dV /dt = αV+U (t), V (t 0)=V 0, t 0 ≤t≤T, (8)

где V – центрированная случайная переменная (ЦСП); α – детерминированная постоянная, U (t) – центрированный белый шум интенсивности U; V0 – значение ЦСП V при t=t0, то дисперсия ЦСП V определяется выражением [2]

V = V0exp (2α (t – t 0))+ +(U/ 2α) (exp(2α(t – t 0))– 1), (9)

где V0 – значение дисперсии V при t=t0. При α= 0 уравнение (8) примет вид

dV /dt =U (t), V(t0)=V0, t0 ≤ t≤ T, (10)

а выражение для дисперсии ЦСП V этого уравнения получим предельным переходом в функции (9) при стремлении α к нулю [2]

V = 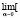V0 exp (2α (t – t0))]+

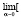+(U / 2α) (exp (2α (t – t 0))– 1)], (11)

которое при раскрытии неопределённости вида 0 / 0 во втором слагаемом принимает вид

V = V 0+U (t–t 0). (12)

Это – первая часть описываемой процедуры. Вторая часть заключается в получении дисперсии W ЦСП W уравнения вида

dW /dt=φ(t)B, W (t 0)=V0, t0≤t≤T, (13)

где φ (t) – детерминированная функция времени (ДФВ), B – ЦСВ с дисперсией B, начальное условие W (t 0) равно начальному условию V(t0). При условии некоррелированности ЦСВ V0 и ЦСВ B дисперсия W определяется выражением

W = V0 +ψ 2(t)B, (14)

где ψ(t) – ДФВ, определяемая решением уравнения

dψ /dt = φ (t), ψ (t 0)= 0, t 0 ≤t≤T. (15)

И наконец, третья часть описываемой процедуры заключается в усреднении на интервале времени наблюдения (УИВН) функций (12), (14), составлении уравнения

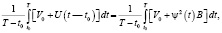(16)

и в решении этого уравнения относительно U, которое принимает вид

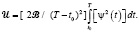(17)

Применяя формулу (17) с учётом решения уравнения (15) к слагаемому gK в уравнении (1), то есть полагая φ(t)=g, B =κ 2 и к слагаемому hL в уравнении (3), то есть полагая φ(t)=h, B = λ2, получаем соответственно:

M= (2 / 3) (gκ)2 (T – t 0),

N= (2 / 3) (h λ)2 (T – t 0), (18)

где символами κ, λ обозначены средние квадратические отклонения (СКО) соответственно ЦСВ K, L:

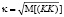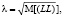, (19)

и где выражениями

M[(KK)]=M[(K)2],

M[(LL)]=M[(L) 2]

обозначены операции МО.

Итак, для решения общей задачи предложено использовать выражение (18) в уравнении (5) в качестве характеристик априорной и измерительной погрешностей, из которых N входит в формулы (6), (7). Очевидно, что принятие этого предложения предполагает доказательство эффективности фильтра (4). В таком доказательстве и заключаются поставленные и решаемые далее частные задачи при введении условий эффективности фильтра: измеряемая информация о процессе должна быть точнее априорной информации, а фильтрованная информация о процессе должна быть точнее измеряемой. Кроме этого, целесообразно ввести условие, выражающее тот факт, что погрешность оценки состояния процесса, дисперсия которой определяется решением уравнения Риккати, должна быть меньше погрешности измеряемой информации. Следует заметить, что для классической задачи оценивания состояния динамических процессов при влиянии шумовых помех это условие является результирующим. В данной работе предложено оставить это условие и ввести дополнительное критериальное условие, характеризующее сравнительную точность ФПС и ИПС. Указанным выше трём условиям соответствуют следующие три количественных критерия эффективности фильтра или, другими словами, эффективности процедуры фильтрации:

fYZ = c η / ζ ≥ f1 > 1, (20)

fZR = ζ /cρ ≥ f2 > 1, (21)

fZX = ζ /c χ ≥ f 3 > 1, (22)

где введены обозначения:

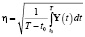, (23)

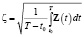, (24)

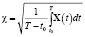, (25)

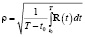, (26)

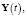
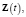
где 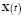– дисперсии соответственно АПС, ИПС, ФПС; 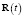– решение уравнения Риккати (5); f 1, f 2, f 3 – желаемые величины соответственно функций сравнения fYZ, fZR, fZX, которыми определяются соответствующие эффекты процедуры фильтрации. Подчёркнутые неравенства в выражениях (20), (21), (22) приведут к ограничениям на параметры a, c, g, h, κ, λ, η 0= 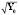, t0, T процесса (1) и измерителя (2). Условие (20) отражает очевидный факт превышения погрешности АПС над погрешностью ИПС, условие (21) требует превышения погрешности ИПС над погрешностью оценки состояния процесса, дисперсия которой определяется решением уравнения Риккати, а условие (22) требует превышения погрешности ИПС над погрешностью ФПС. Этими тремя критериальными ограничениями и «покупаются» указанные эффекты.

Для решения общей задачи необходимо решить следующие частные задачи: 1) выполнить математическое описание для определения ограничений на параметры процесса согласно критериям (20), (21), (22); 2) составить алгоритм и разработать программу на основе выполненного математического описания, включающую параметрический синтез процесса, анализ эффективности процедуры фильтрации и функционирования имитационной модели этой процедуры; 3) сформулировать методику использования полученных результатов при построении реального оптимального фильтра для процессов с математическим описанием (1), (2), (3); 4) предложить методы доведения полученных результатов до их использования для решения задач оценивания состояний динамических процессов с более общим математическим описанием.

Кратко поясним решения каждой из поставленных частных задач.

Математическое описание. Применяем операции центрирования (ОЦ) к уравнениям (1), (4), вводим обозначение для дисперсий АПС Y, ФПС X и корреляционных моментов АПС Y с ЦСВ K, ФПС X с ЦСВ L, составляем системы уравнений относительно указанных дисперсии и корреляционных моментов, решаем эти системы уравнений относительно дисперсий АПС Y, ФПС X и применяем к полученным решениям операции усреднения на интервале времени наблюдения (УИВН), получаем выражение для СКО АПС Y, ФПС X. Находим выражение для дисперсии ИПС Z, применяем к этому выражению операцию УИВН, получаем выражение для СКО ИПС Z. Находим аналитическое решение уравнения (5), применяем к полученному решению операцию УИВН, получаем выражение для СКО погрешности оценки состояния процесса, дисперсия которой определяется уравнением Риккати. После перечисленных выкладок составляем критериальные неравенства (20), (21), (22), которые принимают вид:

fYZ=cη / ζ=c [A00(gκ) 2+A22 η02] 0,5/hλ≥ f1> , (27)

fZR = (hλ) / (c η0) ≥ f2 > 1, (28)

fZX= {2γ(h λ2/ [3(c η 0) 2]– 1}/ (B22– 2B11+1)0,5≥ ≥ f3> 1, (29)

где η 0 – СКО АПС Y при t= t0 и введены обозначения:

A00=A22 – 2A11+ 1, A22= (exp (2γ) – 1)/ 2γ,

A11= (expγ – 1)/γ, γ=a τ, τ=T – t0,

B11=(expβ – 1)/β,

B22=(exp 2β – 1) / 2β, b=a–pc, β=b τ. (30)

Кроме выполнения критериальных неравенств (27), (28), (29), потребуем, чтобы параметры удовлетворяли уравнению:

[2(h λ)2 / (3c 2)]aτ{1+ [ 1+ (cgκ/ah λ) 2]0,5}= =η02, (31)

Выполненным математическим описанием доказана теорема: для того, чтобы в процессе с математическим описанием (1), (2), (3) УИВН СКО АПС превышало УИВН СКО ИПС не менее, чем в f1 раз и УИВН СКО ИПС превышало погрешность оценки состояния процесса, определяемой корнем квадратным из УИВН решения уравнения Риккати, не менее, чем в f2 раз и УИВН СКО ИПС превышало УИВН СКО ФПС не менее, чем в f3 раз, необходимо, чтобы параметры этого процесса удовлетворяли уравнению (31) и неравенствам (27), (28), (29) с учётом обозначений (30). Доказательство достаточности этой теоремы следует выполнять реализацией процедур анализа эффектов фильтрации и анализа функционирования имитационной модели фильтрации путём варьирования параметров в пределах найденных ниже допустимых интервалов их изменения до достижения выполнения критериальных неравенств.

На основе доказанной теоремы определены допустимые (в смысле достижения указанных выше эффектов) интервалы изменения параметров процесса:

0<a< 3 / (4 τf 2 2), (32)

a [(a12+a0)0,5–a1]0,5/κ<g<

<aθ0{[θ0/(η0f 2)]2–2}0,5/κ, (33)

c η0 f2<h< сvB/ λ, (34)

где введены обозначения:

θ0 = η0(3/ 2γ)0,5,

a 0=θ0 (f12θ02– 2A22 η02) /A00,

a1= θ02+ (A22 η02 /A00) (35)

и параметр vB определяется в алгоритме реализацией специальной итерационной процедуры.

Процедуру определения ограничений на параметры процесса назовём параметрическим синтезом. Процедуру определения критериальных функций fYZ, fZR, fZX при синтезированных параметрах назовём анализом эффектов фильтрации.

Целью частной задачи построения имитационной модели функционирования процедуры фильтрации процесса является подтверждение наличия эффектов фильтрации, обеспечиваемых параметрическим синтезом и их анализом, путём исследования случайных процессов при заданном законе распределения СВ получения априорной, измеряемой и фильтрованной переменных состояния. Первая часть этой задачи заключается в получении величин вида:

FYZc = cY*c /Z*c, FZXc = Z*c /cX*c, (36)

где Y*с, Z*c, X*c – соответственно модули границ симметричных интервалов, в которые попадают при заданных вероятностях PY, PZ, PX и СКО η, ζ, χ центрированные составляющие априорной, измеряемой и фильтрованной переменных состояния процесса, обусловленных наличием на входе ЦСВ Y0c – погрешностью начального условия для переменной Y, K – погрешностью задания априорной информации о процессе, L – погрешностью задания измеряемой информации при нормальном законе распределения случайных величин. Для входных ЦСВ Y0c, K, L их СКО η 0, κ, λ заданы и, следовательно, однозначно определяются соответствующие аргументы нормированной функции Лапласа (НФЛ). Сравнивая величины (36) соответственно с величинами f1, f3, делаем вывод о наличии желаемых эффектов фильтрации. Вторая часть построения имитационной модели процедуры фильтрации заключается в анализе изменения процесса во времени при задании имитации измеряемой переменной Z(t,L) и определении фильтрованной переменной X (t,L), априорной переменной Y(t,K) при синтезированных параметрах процесса при его наблюдении на интервале времени [t 0;T ] и изменении входных ЦСВ K, L соответственно на интервалах [–K*;K* ], [–L*; L* ] с заданными шагами по времени Δt и по ЦСВ ΔK, ΔL. Математическое описание этой процедуры включает в себя:

1) модель ЭПС

dy /dt=ay+u, y (t0)=y 0, t0≤t≤T, (37)

2) модель ИПС

z=cy+hL, t0≤t≤T, (38)

3) модель АПС

dY /dt=aY+u+gK, Y (t 0)=Y 0, t0≤t≤T, (39)

4) модель ФПС

dX /dt=aX+p (Z–cX)+u,

X(t 0)=y 0, t0≤t≤T. (40)

На основе этих моделей составляем алгоритм численных решений, после реализации которого и анализа полученных решений делаем вывод о реальной эффективности процедуры фильтрации в смысле принятых критериев (20), (22) при синтезированных параметрах процесса, то есть доказываем достаточность сформулированной выше теоремы. Следует заметить, что основной параметр p фильтра зависит и от независимых параметров c, κ, λ и от синтезированных параметров g, h. Это замечание относится и к параметру b.

Реальные погрешности априорной информации целесообразно из соображения адекватности задавать в виде относительных величин соответственно DY,, DZ,которые связаны с СКО gκ, h λ зависимостями:

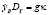, yBDZ = h λ, (41)

где введены обозначения для модулей наибольших значений ИПС и её производной по времени:

yB =|sup {y (t), t0 ≤t≤T}|, (42)

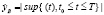. (43)

В результате решения задачи параметрического синтеза определены граничные значения gL, gB параметра g и граничные значения hL, hB параметра h. Использовав зависимости (41), запишем выражения для соответствующих граничных значений относительных погрешностей DY, DZ: DYL= (gL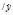B)κ,

DYB= (gB /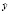B)κ, DZL= (hL /yB) λ,

DZB= (hB /yB) λ. (44)

Задавая реальные относительные погрешности DY*, DZ* и получая граничные значения (46) этих же погрешностей, удовлетворяющих синтезированным параметрам процесса, определяем попадание или непопадание заданных относительных погрешностей в интервалы [DYL; DYB ], [DZL; DZB ] и делаем вывод о реальности применения процедуры фильтрации к рассматриваемому процессу.

Алгоритм и пакет программ. На основе выполненного математического описания составлен алгоритм и разработан пакет программ [4] для численного решения задач параметрического синтеза, анализа эффектов фильтрации и анализа функционирования имитационной модели динамического процесса с математическим описанием (1) – (3).

Методика. Оценивание состояния динамических процессов с математическим описанием (1)–(3) осуществляется следующей последовательностью действий: 1) задать: 1.1) желаемые величины критериев эффективности процесса; 1.2) относительные погрешности априорной и измеряемой информации в виде допустимых интервалов их изменения; 1.3) интервал изменения основного параметра a процесса; 1.4) независимые параметры процесса: t0, T, ξ, κ, λ, uB; 2) используя разработанный пакет программ, реализовать процедуры: 2.1) параметрического синтеза процесса, то есть определения интервалов изменения параметров a, g, h из условий удовлетворения заданным критериям эффективности; 2.2) анализа эффектов фильтрации, то есть определения величин критериев при синтезированных значениях интервалов изменения параметров a, g, h; 2.3) анализа имитационной модели фильтрации, то есть определения: 2.3.а) величин критериев при заданных значениях параметров a, g, h из их синтезированных интервалов изменения и заданных входных ЦСВ K, L, Yc0 с заданными законами распределения и вероятностями попадания их значений в симметричный интервал; 2.3.б) функций времени эталонной, априорной, измеряемой и фильтрованной переменных состояния процесса; 3) проанализировать полученные результаты оценивания динамического процесса и сделать вывод о целесообразности использования их в заданном реальном процессе; 4) если показана целесообразность использования полученных результатов в заданном реальном процессе, то использовать результаты пунктов 2.1) и 2.2) этой методики для разработки программы мобильного (бортового) компьютера, реализующей процедуру оценивания заданного реального процесса на основе реальных априорной информации и реальной измеряемой информации о его состоянии.

Обобщения. Использовать результаты данной работы для решения задач оценивания состояния динамических процессов с более общим математическим описанием возможно при учёте следующих замечаний:

1. В работе рассмотрены одномерные процессы с математическим описанием (1)–(3), в которых параметры a, g, h являются положительными и постоянными. Используя предложенный в работе метод параметрического синтеза, возможно решать задачи параметрического синтеза для процессов с математическим описанием (1)–(3), но с параметрами a, g, h, которые могут быть как положительными, так и отрицательными, а значит, кроме рассмотренного в работе варианта положительности указанных параметров, следует рассмотреть ещё и варианты сочетаний положительности и отрицательности указанных параметров: 1) a> 0, g< 0, h> 0; 2) a> 0, g< 0, h< 0; 3) a< 0, g> 0, h> 0; 4) a< 0, g< 0, h> 0; 5) a< 0, g< 0, h< 0.

2. В случае одномерных процессов с переменными во времени параметрами a, g, h, заданных функциями времени на интервале [t 0; T ] следует определить их усреднённые значения на этом интервале, затем использовать предложенные в работе методы синтеза и анализа при найденных усреднённых значениях указанных параметров, а имитационную модель процедуры фильтрации построить для исходных переменных во времени параметров. Анализируя результаты функционирования построенной таким образом имитационной модели по полученным величинам эффектов фильтрации, следует сделать вывод о целесообразности использования предложенного метода в этом случае, то есть для одномерных процессов с переменными во времени параметрами.

3. Для случая многомерных процессов с постоянными параметрами следует: 1) используя аппарат теории матриц, выполнить математические описания процессов с параметрами aij ckj, gil, hkm, где i,j= 1,…,N 1, k= 1,…,N 2, l= 1,…,N 3, m= 1,…,N 4 и где: N1 – количество АПС, N2 – количество ИПС, N3 – количество ЦСВ – погрешностей АПС, N4 – количество ЦСВ – погрешностей ИПС; 2) составить критериальные ограничения на указанные параметры в виде условий:

fYZk = ckk ηk / ζk ≥ fYZ*k, k= 1,…,N 2; (45)

fZRk = ζk /ckk ρk ≥ f ZR*k, k= 1,…,N 2; (46)

fZXk = ζk /ckkχk ≥ f ZX*k, k= 1,…,N 2; (47)

fYXk = ηi /χi ≥ f YX*k, i= 1,…,N 1; (48)

fRXk = ρi /χi ≥f YX*k, i= 1,…,N 1, (49)

где ηi, ζk, χi – усреднённые на интервале времени [t 0; T] СКО соответственно АПС, ИПС, ФПС; ρi – СКО решения системы уравнений Риккати; 3) найти численные решения системы (3N 2+ 2N 1) неравенств относительно синтезируемых параметров, то есть найти допустимые в смысле критериальных неравенств (45)–(49) интервалы изменения этих параметров; 4) решить задачи анализа эффектов фильтрации для синтезированных параметров; 5) реализовать алгоритм функционирования имитационной модели процедуры фильтрации; 6) сделать вывод о целесообразности применения предложенного метода в этом случае.

4. Для случая многомерных процессов с переменными во времени параметрами, заданными в виде ограниченных функций времени на интервале [t 0; T ], следует выполнить процедуру усреднения этих параметров на этом интервале и выполнить процедуры пунктов 1)–4) замечания 3 для усреднённых параметров и далее: 5) на основе синтезированных усреднённых параметров определить реальные зависимости во времени этих параметров, удовлетворяющих заданным допустимым ограниченным интервалам изменения функций времени этих параметров; 6) реализовать алгоритм функционирования имитационной модели процедуры фильтрации для переменных во времени параметров, определяемых зависимостями, полученными в пункте 5) этого замечания; 7) сделать вывод о целесообразности использования предложенного метода для оценивания заданного многомерного динамического процесса с переменными во времени параметрами.

5. Для случая нелинейных многомерных процессов с переменными во времени параметрами следует применить линеаризацию нелинейностей в системе уравнений относительно АПС и в зависимостях для ИПС, зафиксировать ограничения на параметры после указанных процедур линеаризации и затем использовать процедуры замечания 4.

Библиографическая ссылка